<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Un <strong>miroir plan</strong> est une surface polie très lisse sur laquelle la lumière subit une </span><span><a href="/fr/eleves/bv/physique/physique-la-reflexion-p1032#speculaire">réflexion spéculaire</a>. </span></p>
</body></html>
Bien qu'un miroir plan ait la capacité de produire une image claire d'un objet, d'autres surfaces peuvent également produire des images du même type qu'un miroir plan.
Un liquide très calme, comme un lac sans vague, peut également agir comme un miroir plan.
Le champ de vision d’un miroir plan est l’espace que peut percevoir un observateur en regardant dans le miroir.
Il est possible de déterminer le champ de vision en utilisant les lois de réflexion. Il suffit de suivre les étapes suivantes pour observer le champ de vision dans un miroir plan.
1. À partir de l'observateur, dessiner des rayons lumineux partant des extrémités du miroir plan et qui se rendent jusqu'à l'oeil.
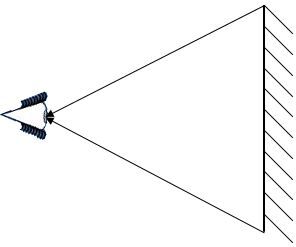
2. Dessiner des normales à chacun des points d'incidence.
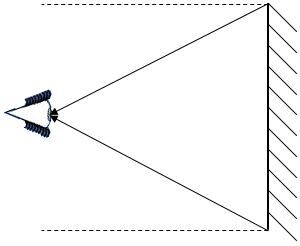
3. Dessiner les rayons incidents en respectant la loi de la réflexion.
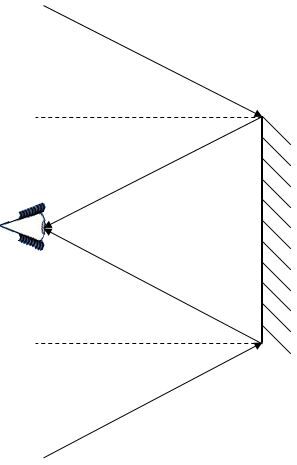
4. Tout ce qui se trouve entre les rayons incidents fait partie du champ de vision de l'observateur.
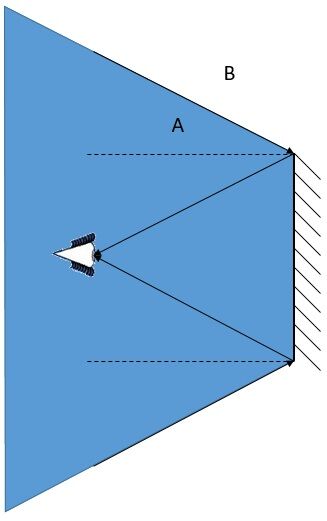
En se basant sur l’illustration précédente, il est possible de déduire que l’objet A serait inclus dans le champ de vision de l’observateur, alors que l’objet B serait à l’extérieur du champ de vision.
Cette technique peut être utilisée peu importe la position de l'observateur, qu'il soit devant ou à côté du miroir.
Pour augmenter le champ de vision dans un miroir plan, il est possible de modifier certains paramètres:
- Augmenter la grandeur du miroir. En choisissant un miroir plus grand, les angles d'incidence et de réflexion augmenteront, ce qui augmentera le champ de vision.
- Rapprocher l'observateur du miroir. Les angles d'incidence et de réflexion augmenteront également, ce qui augmentera le champ de vision.
- Utiliser un miroir convexe.
Une personne de |\small \text {1,80 m}| se regarde dans le miroir. Ses yeux se trouvent |\small \text {10 cm}| au-dessous de son crâne. Quelle doit être la grandeur minimale du miroir pour qu'il puisse se voir en entier?
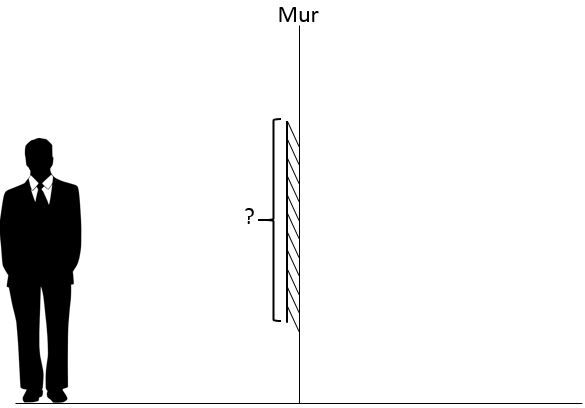
Pour trouver la grandeur du miroir, il faut tout d'abord savoir que l'image de la personne sera à égale distance du côté opposé de l'observateur.

Une droite perpendiculaire (une normale) doit ensuite être dessinée à la hauteur des yeux de l'observateur.
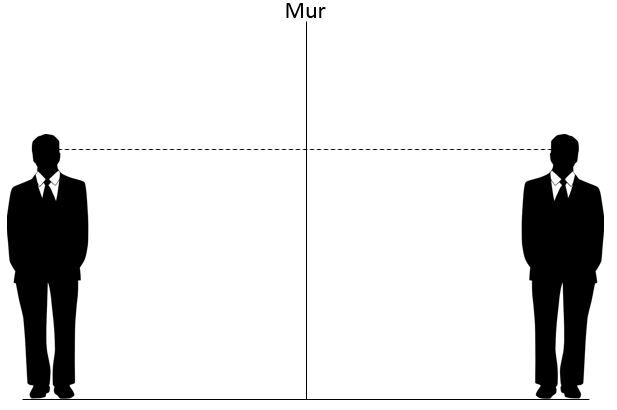
La prochaine étape consiste à dessiner un rayon partant des pieds de l'observateur orienté vers les yeux de l'image. Ceci représente un rayon incident.
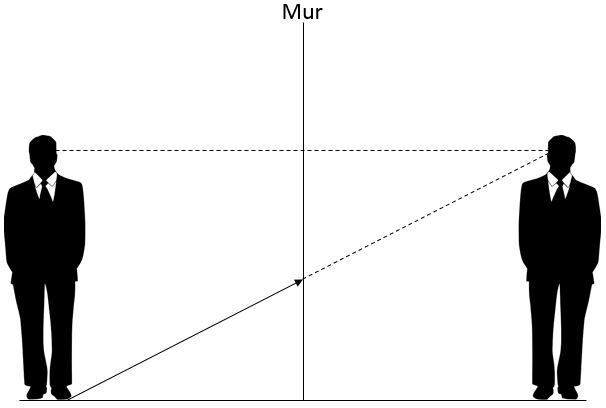
Il faut ensuite procéder à la réflexion de ce rayon en suivant les lois de la réflexion. Le rayon réfléchi atteindra les yeux de l'observateur.
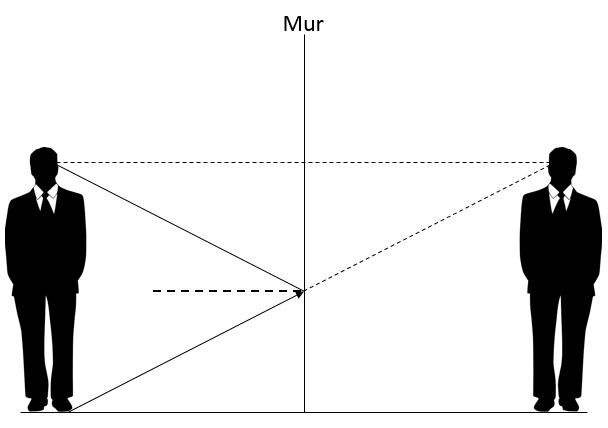
En dessinant le rayon réfléchi, deux triangles ont été formés. Ces deux triangles sont isométriques. Ainsi, il est possible de déterminer que pour voir la partie inférieure du corps, le miroir doit mesurer la moitié de la partie inférieure de l'observateur.
|\text {1,80 m - 0,10 m = 1,70 m}|
|\displaystyle \frac {\text {1,70 m}}{2} = \text {0,85 m}|
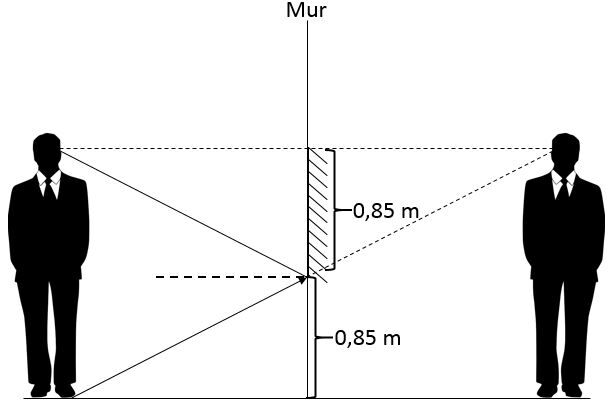
La hauteur du miroir pour voir la partie inférieure de l'observateur est donc |\text {0,85 m}|. La partie inférieure du miroir doit être placée à |\text {0,85 m}| du sol.
Il faut répéter l'opération pour la partie supérieure (entre les yeux et le dessus de la tête).
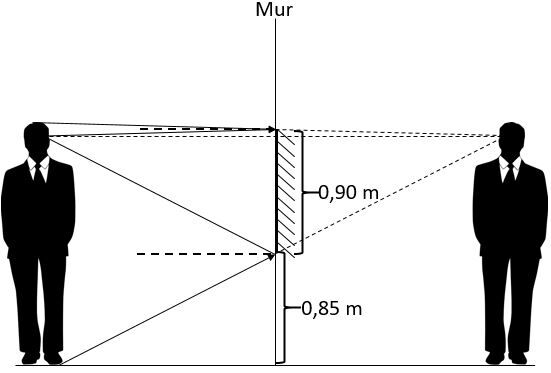
Il faut donc un miroir mesurant la moitié de la distance entre la tête et les yeux, soit |\text {0,05 m}|. En additionnant ce miroir à celui nécessaire pour voir la partie inférieure du corps, il faut donc un miroir de |\text {0,90 m}| pour voir le corps au complet.
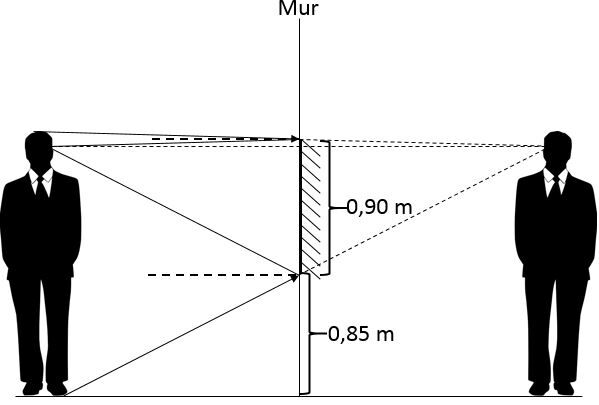
Donc, pour que l'observateur puisse se voir au complet dans un miroir, il doit installer un miroir de |\text {90 cm}| de grandeur situé à |\text {85 cm}| du sol.
Source de l'image de l'observateur
Il est logique de dire qu’un rayon réfléchi par un miroir aura une trajectoire différente si le miroir subit une rotation.
Lorsqu'un miroir subit une rotation d'un angle déterminé, le rayon réfléchi sera dévié du double de cet angle par rapport à sa position initiale.
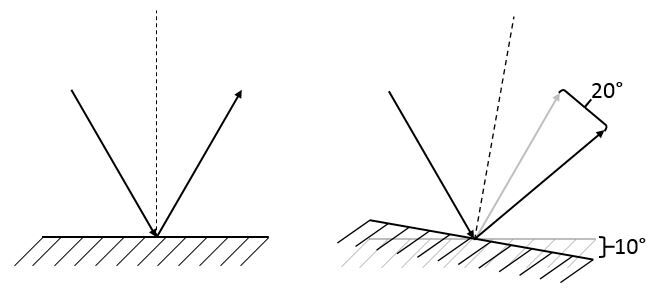
Lorsque le miroir tourne, la normale, qui doit toujours être perpendiculaire au miroir, tourne nécessairement du même angle. Comme le rayon incident ne bouge pas, l’angle d'incidence augmentera du même angle que la rotation du miroir.
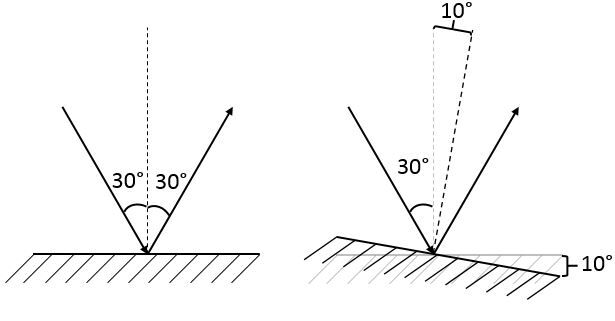
Dans l'exemple ci-dessus, l'angle d'incidence est maintenant de |\small \text {40}^{\circ}|. Pour que la loi de la réflexion soit respectée, l'angle de réflexion devra donc être de |\small \text {40}^{\circ}|. Toutefois, puisque la normale a été déplacée, le rayon réfléchi devra également être déplacé pour qu'il puisse être mesuré par rapport à la nouvelle normale.
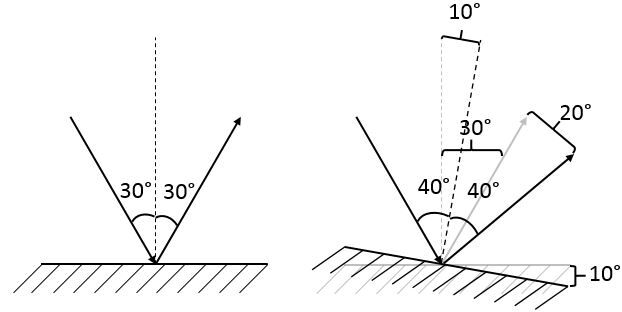
Finalement, l’angle de rotation du miroir aura été ajouté deux fois (du côté incident et du côté réfléchi) et donc, la déviation du rayon réfléchi sera égale au double de la déviation du miroir.
Pour trouver le nombre d'images formées par deux miroirs plans, la formule suivante doit être utilisée:
|N=\displaystyle \left( \frac {360^{\circ}}{\theta}\right) - 1|
N représente le nombre d'images formées
|\theta| représente l'angle entre les miroirs |(\small ^{\circ})|
L'angle entre les deux miroirs fait donc varier le nombre d'images pouvant être obtenues. Ainsi, plus l'angle s'approche de |\small \text {0}^{\circ}|, plus le nombre d'images formées s'approche de l'infini. Il est à noter que le nombre d'images est infini lorsque les miroirs sont parallèles.
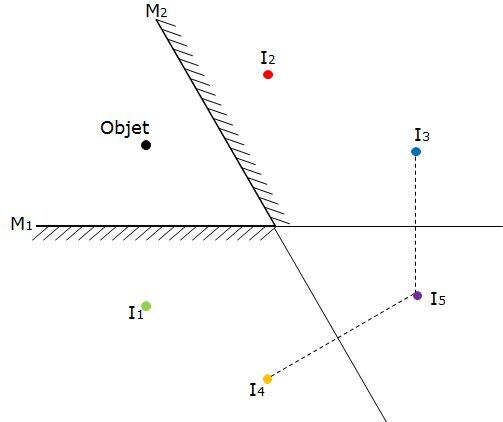
Un angle de |\small \text {60}^{\circ}| entre les deux miroirs provoque la formation de cinq images.
||\begin{align} N=\displaystyle \left( \frac {360^{\circ}}{\theta}\right) - 1 \quad \Rightarrow \quad N &= \displaystyle \left(\frac {360^{\circ}}{60^{\circ}}\right) - 1 \\ \\ &= 6 - 1 \\ \\ &= 5 \end{align}||
Pour obtenir ces images, il faut utiliser les lois de la réflexion. La première image obtenue est l'image de l'objet dans le premier miroir (représenté en vert sur le schéma ci-dessous). La deuxième image est l'image de l'objet représenté dans le deuxième miroir (représenté en rouge sur le schéma ci-dessous).
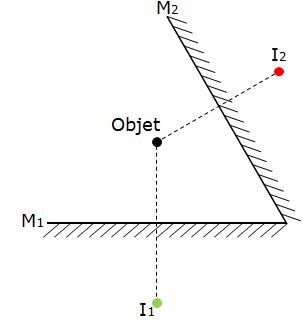
La troisième image est obtenue en dessinant la réflexion de la première image dans le deuxième miroir (représenté en bleu dans le schéma ci-dessous). Il est possible de prolonger, au besoin, les miroirs afin de représenter adéquatement l'objet.
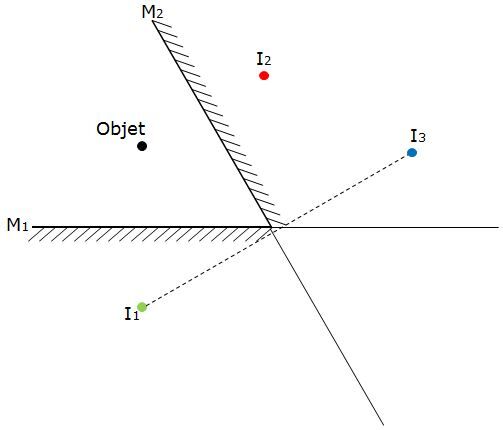
La quatrième image est obtenue en dessinant la réflexion de la deuxième image dans le premier miroir (représenté en orange dans le schéma ci-dessous).
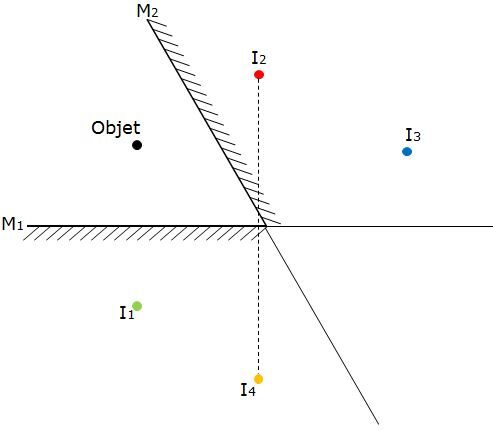
La dernière image est obtenue en représentant l'image obtenue par la réflexion de la troisième image et de la quatrième image. Le point de rencontre forme la cinquième image, représentée en violet dans le schéma ci-dessous.