A plane mirror is a very smooth polished surface on which light undergoes specular reflection.
Although a plane mirror has the ability to produce a clear image of an object, other surfaces may also produce images of the same type as a plane mirror.
A very still liquid, such as a lake without a wave, is also capable of acting as a plane mirror.
The field of view of a plane mirror is the space that an observer can perceive when looking in the mirror.
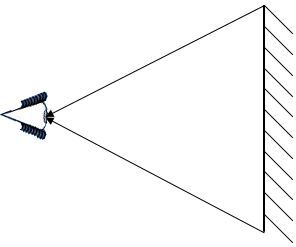
It is possible to determine the field of view using the laws of reflection. Simply follow the steps below to observe the field of view in a plane mirror.
-
Draw light rays from the ends of the plane mirror converging towards the eye of the observer.
-
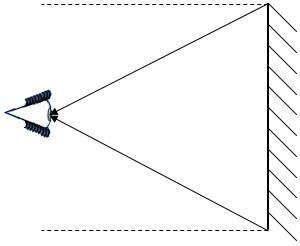
Draw normals at each point of incidence.
-
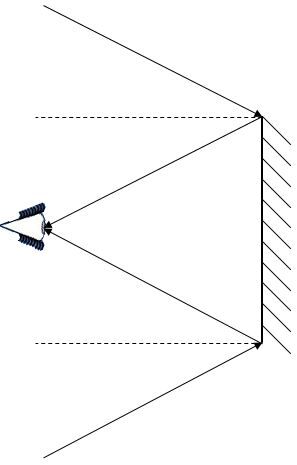
Draw the incident rays while observing the law of reflection.
-
Everything between the incident rays is part of the observer's field of view.
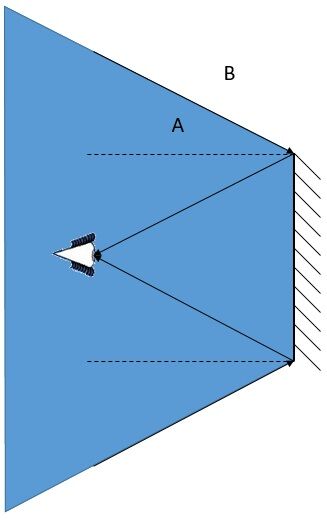
Based on the previous illustration, it is possible to deduce that object |A| would be within the observer's field of view, while object |B| would be outside their field of view.
This technique can be used regardless of the viewer's position, whether in front of or next to the mirror.
To increase the field of vision in a plane mirror, it is possible to modify certain parameters:
-
increase the size of the mirror. By choosing a larger mirror, the angles of incidence and reflection will increase, thus widening the field of view;
-
bring the observer closer to the mirror. The angles of incidence and reflection will also increase, which will expand the field of view;
-
use a convex mirror.
A person who is |1.80\ \text {m}| tall looks in the mirror. Their eyes lie |10\ \text {cm}| below the top of their head. What must be the minimum size of the mirror for the person to be able to see their whole self?
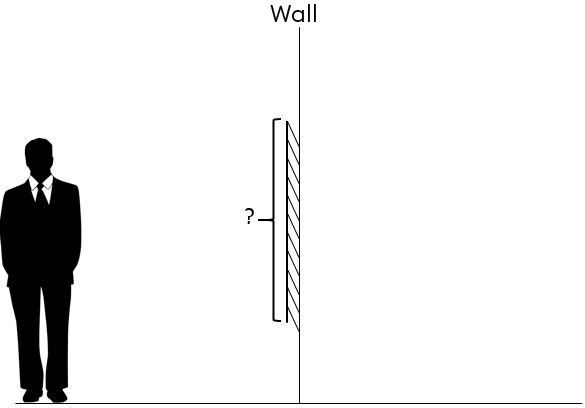
To find the size of the mirror, we must first know that the image of the person will be at equal distance from the opposite side of the observer.
A perpendicular line (a normal) should then be drawn at the level of the observer's eyes.

The next step is to draw a ray from the observer's feet pointing towards the eyes in the image. This is an incident ray.

This ray must then be reflected according to the laws of reflection. The reflected ray will reach the observer’s eyes.
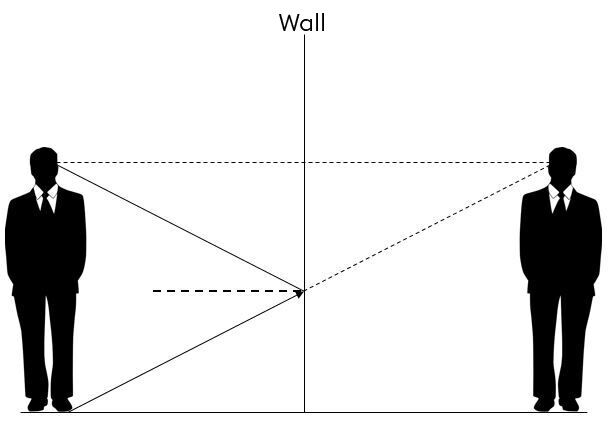
By drawing the reflected ray, two triangles have been formed. These two triangles are isometric. Thus, it is possible to determine that in order for the observer to see the lower half of their body, the mirror must be half the size of the observer’s lower half.
||1.80\ \text{m} - 0.10\ \text{m} = 1.70\ \text{m}}||
||\dfrac {1.70\ \text {m}}{2} = 0.85\ \text {m}||
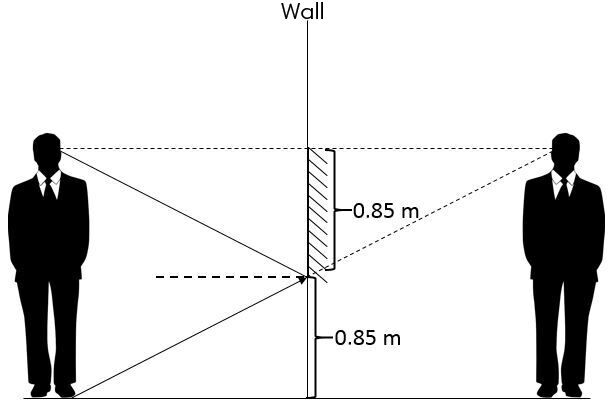
For the observer to see the lower half of their body, the height of the mirror must therefore be |0.85 \ \text {m}.| The lower part of the mirror should be placed |0.85\ \text {m}| from the ground.
We must repeat the procedure for the upper part (between the eyes and the top of the head).
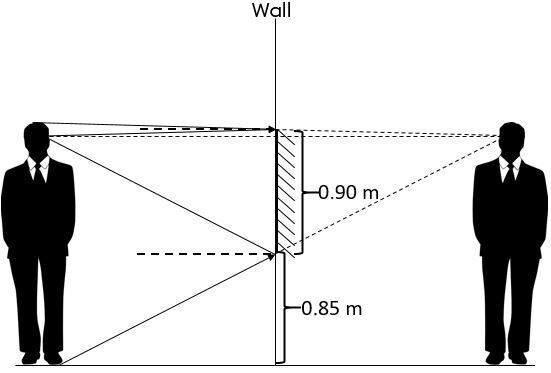
At this stage, a mirror measuring half the distance from the head to the eyes is required, which is |0.05\ \text {m}.| Thus, in order for the observer to see their whole body, the mirror has to measure |0.90\ \text {m}.|

So, for the observer to be able to see their whole body completely in a mirror, they must set up a mirror of |90\ \text {cm}| located |85\ \text {cm}| from the ground.
Source of the observer image
It makes sense to say that a ray reflected from a mirror will have a different path if the mirror is rotated.
When a mirror undergoes a rotation of a determined angle, the reflected ray will be deviated by twice this angle compared to its initial position.
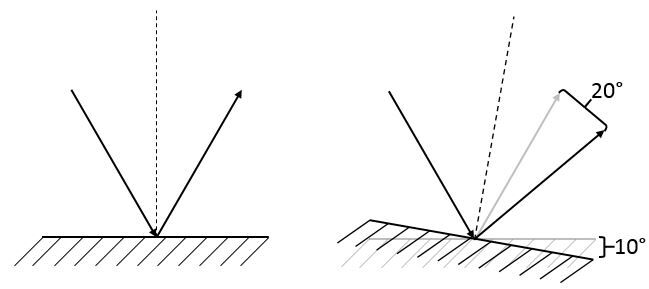
When the mirror rotates, the normal, which must always be perpendicular to the mirror, necessarily rotates by the same angle. As the incident ray does not move, the angle of incidence will increase by the same angle as the rotation of the mirror.
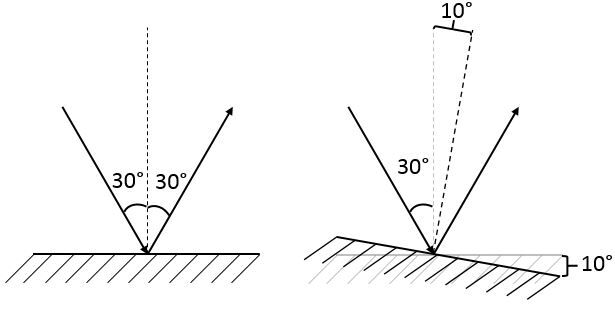
In the example above, the angle of incidence is now |\text {40}^{\circ}|. For the law of reflection to be observed, the angle of reflection must therefore be |\text {40}^{\circ}|. However, because the normal has been moved, the reflected ray will also need to be moved so that it can be measured relative to the new normal.
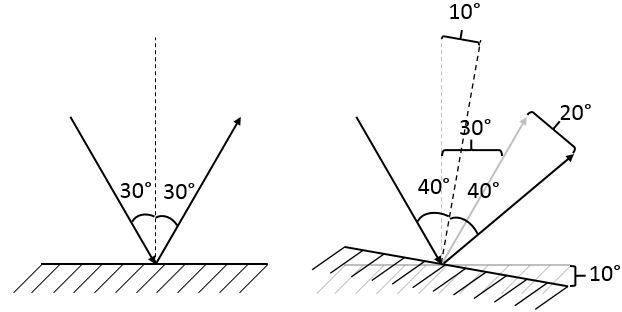
Finally, the angle of rotation of the mirror will have been added twice (on the incident side and on the reflected side). Therefore, the deviation of the reflected ray will equal twice the deviation of the mirror.
To find the number of images formed by two plane mirrors, the following formula should be used.
|N=\left(\dfrac {360^{\circ}}{\theta}\right) - 1|
|N| stands for the number of images formed.
|\theta| stands for the angle between the mirrors |(\small ^{\circ}).|
The angle between the two mirrors therefore makes the number of images that can be obtained vary. Thus, the closer the angle is to |\text {0}^{\circ}|, the closer the number of images is to infinity. Note that the number of images is infinite when the mirrors are parallel.
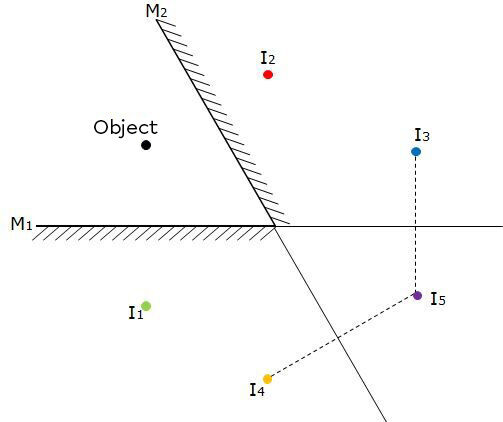
An angle of |\text {60}^{\circ}| between the two mirrors results in the formation of five images.
||\begin{align} N=\left(\dfrac {360^{\circ}}{\theta}\right) - 1 \quad \Rightarrow \quad N &=\left(\dfrac {360^{\circ}}{60^{\circ}}\right) - 1 \\ \\ &= 6 - 1 \\ \\ &= 5 \end{align}||
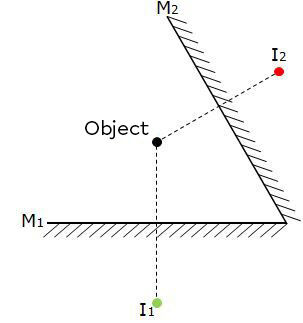
To obtain these images, we must use the laws of reflection. The first image obtained is the image of the object in the first mirror (shown in green on the diagram below). The second image is the image of the object represented in the second mirror (illustrated in red in the diagram below).
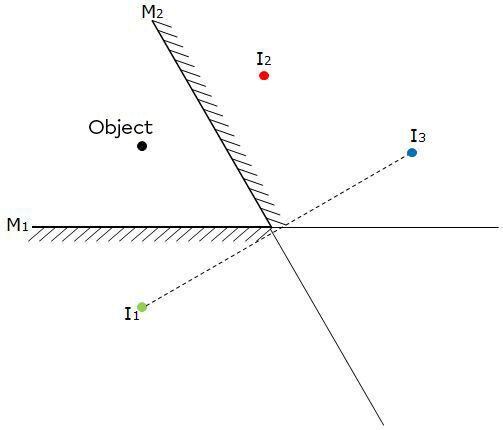
The third image is obtained by drawing the reflection of the first image in the second mirror (shown in blue in the diagram below). It is possible to extend the mirrors, if necessary, to adequately represent the object.
The fourth image is obtained by drawing the reflection of the second image in the first mirror (shown in orange in the diagram below).
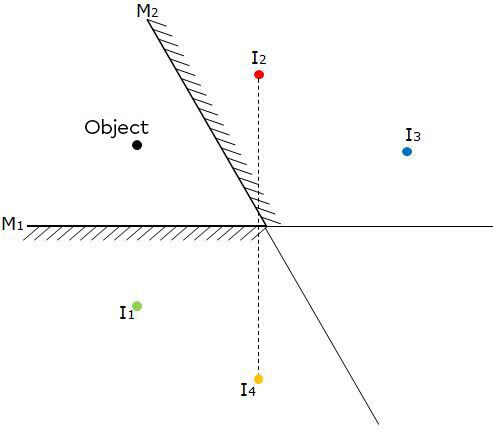
The last image is achieved by representing the image obtained by the reflection of the third and fourth images. The intersecting point forms the fifth image, shown in purple in the diagram below.