La pression est une force appliquée sur une surface.
Pour déterminer la pression exercée sur un objet, il faut utiliser la formule suivante:
|P= \displaystyle \frac{F}{A}|
où
P représente la pression en Pascal (Pa)
F représente la force en Newtons (N)
A représente la surface sur laquelle la force est appliquée en mètres carré (m2)
Quelle est la pression exercée par un livre qui exerce une force de 20 N sur une table et qui mesure 10 cm par 30 cm ?
Il faut tout d'abord trouver la surface du livre en m2.
|10cm = 0,1m|
|30cm = 0,3m|
|A_{rectangle} = b \times h|
|A_{rectangle} = 0,1 m \times 0,3 m|
|A_{rectangle} = 0,03 m^{2}|
Il faut ensuite déterminer la pression à l'aide de la formule écrite dans l'encadré ci-dessus.
|P=\displaystyle \frac{F}{A}|
|P=\displaystyle \frac{20N}{0,03m^{2}}|
|P= 666,67 Pa|
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Sur la Terre, à cause de la gravité, l'air qui nous entoure exerce une pression que l'on nomme <a href="/fr/eleves/bv/sciences/la-pression-atmospherique-et-l-humidite-relative-s1362">pression atmosphérique</a>. </p>
</body></html>
Deux facteurs influencent la pression exercée par un objet.
Plus un objet a une masse importante, plus la force gravitationnelle qu’il exerce est grande. Si la force qu’il exerce est plus grande, la pression qu'il exerce est plus grande également.
Deux personnes marchent dans la neige, la personne qui a une masse plus grande s'enfonce plus profondément dans la neige que la personne qui a une masse plus petite.

Si la force est exercée sur une surface plus grande, la pression sera moins importante.
Une personne marche dans la neige. Si elle utilise des raquettes pour marcher dans la neige, elle s'enfoncera moins, car sa masse se répartit sur une surface plus grande que son pied.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
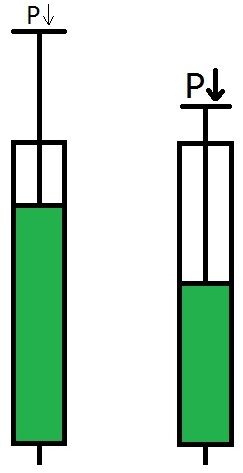
<html><body><p><span>Dans un fluide compressible, la pression est <a href="/fr/eleves/bv/mathematiques/les-situations-de-proportionnalite-m1065">inversement proportionnelle</a> au volume.<br>
|P \alpha \displaystyle \frac{1}{V}|</span></p>
<p> </p>
</body></html>
Si la pression augmente, le volume diminue et vice versa.
Dans une pompe à bicyclette, si une faible pression est exercée sur le piston, le volume sera grand. Toutefois, si le piston est comprimé, la pression augmentera, ce qui fera diminuer le volume.