Diffusion is the process by which a substance mixes with one or more other substances through the movement of its particles.
Effusion is the process by which a gas passes through a small opening.
According to the kinetic theory, gas particles displace in a straight line and frequently collide. Moreover, they also collide with the walls of the container in which they find themselves. This displacement explains two types of phenomenon: diffusion and effusion. Moreover, the rate at which these phenomena occur can be quantified using Graham's Law.
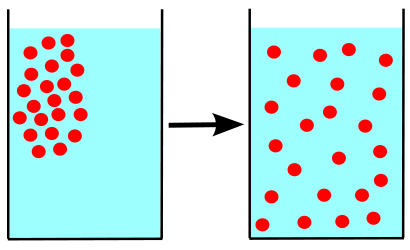
After a while, the random dispersion of the particles results in a uniform distribution throughout the container. This phenomenon is called diffusion. In other words, it's a gradual process whereby a gas spreads throughout the space available to it. A gas can also mix with other gases through the motion of its particles. Diffusion explains why an atmospheric pollutant can spread over large areas, or why certain fragrances invade a room and then disappear.
Representation of the diffusion phenomenon: a gas concentrated in one place (left) is distributed uniformly throughout the available space (right) by diffusion.
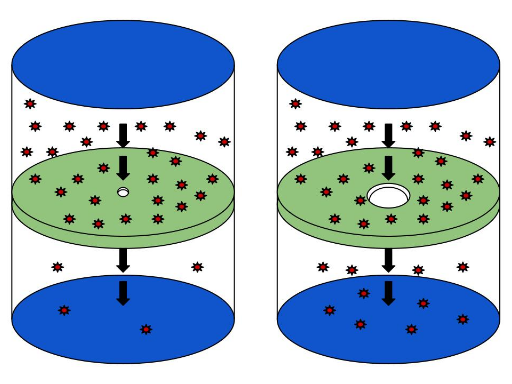
Some containers, rather than being hermetically sealed, have porous walls, i.e. walls with tiny holes. Gas particles can then, by chance of collision, pass through these small openings and escape into the environment. This is known as effusion. A slowly deflating helium balloon is an example of effusion. Oxygen and carbon dioxide passing through the walls of capillaries is another.
Effusion, the passage of gas particles through a membrane, occurs more rapidly with a large opening (right) than with a small one (left).
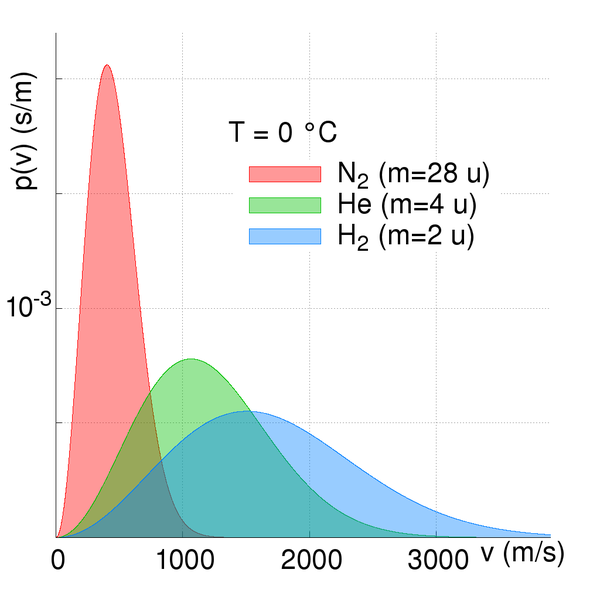
The rate of effusion or diffusion is not the same for all gases. This rate depends mainly on the mass of the particles. Indeed, at a given temperature, all particles have the same amount of kinetic energy. This energy depends on the mass and velocity of the particles. As different gases are made up of particles of different masses, their average velocity will be different. Thus, particles with higher masses diffuse more slowly than light particles, because they travelled more slowly.
Velocity distribution curve as a function of mass: a heavier gas like dinitrogen travels more slowly than a lighter gas like hydrogen.
Graham's law states that the rate of diffusion or the rate of effusion of two gases at the same temperature and pressure conditions are inversely proportional to the square root of their molar masses.
In 1840, the Scottish chemist Thomas Graham posited that, for equivalent conditions of temperature and pressure, the kinetic energies of two gases were equal. Since kinetic energy is a function of particle mass and velocity, he was able to derive the following law:
|\displaystyle \frac{V_{1}}{V_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}|
where
|V_{1}| = rate of diffusion or effusion of gas 1 (in m/s or mL/s)
|V_{2}| = rate of diffusion or effusion of gas 2 (in m/s or mL/s)
|M_{1}| = molar mass of gas 1 (in g/mol)
|M_{2}| = molar mass of gas 2 (in g/mol)
Note: In Graham's law, the molar masses of gases 1 and 2 could be replaced by their masses in grams.
This law states that, under identical temperature and pressure conditions, the rate of diffusion of two gases are inversely proportional to the square roots of their molar masses. This law can also be applied to the rate of effusion of a gas. Graham's law is consistent with the kinetic theory, since the lighter the particles in a gas, the faster they travelled. Lighter gas particles diffuse faster into another gas than heavier ones.
What is the molar mass of an unknown gas Z that diffuses at 700 mL/min in a diffusion device, while methane, |CH_{4}|, diffuses at 350 mL/min in the same device?
- Identification of problem data or values
|V_{1}| = 700 mL/min for the unknown gas Z
|V_{2}| = 350 mL/min for the |CH_{4}|
|M_{1} = x| for the unknown gas Z
|M_{2}| = 16 g/mol for the |CH_{4}| - Molar mass calculation
|\displaystyle \frac{V_{1}}{V_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}|
|\displaystyle \frac{700\ mL/min}{350\ mL/min}=\sqrt{\frac{16\ g/mol}{x}}|
|x=4\ g/mol|
Answer: The molar mass of the unknown gas Z is 4 g/mol.