La diffusion est un processus par lequel une substance se mélange à une ou plusieurs autres substances grâce au mouvement des particules qui les constituent.
L'effusion est un processus par lequel un gaz passe au travers d'une paroi par un petit trou.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Selon la <a href="/fr/eleves/bv/chimie/la-theorie-cinetique-des-gaz-c1004">théorie cinétique des gaz</a>, les particules de gaz se déplacent en ligne droite et se heurtent fréquemment. De plus, elles entrent aussi en collision avec les parois du contenant dans lequel elles se trouvent. Ce déplacement permet d'expliquer deux types de phénomènes: la diffusion et l'effusion. De plus, on peut quantifier le rythme de ces phénomènes à l'aide de la loi de Graham.</p>
</body></html>
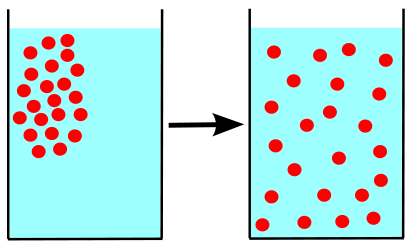
La dispersion aléatoire des particules permet, au bout d'un certain temps, une distribution uniforme des particules de gaz dans tout le contenant qui les renferme. Ce phénomène se nomme diffusion. Ainsi, il s'agit d'un processus graduel lors duquel un gaz se répartit dans tout l'espace qui lui est disponible. Un gaz peut aussi se mélanger à d'autres gaz grâce au mouvement de ses particules. La diffusion permet d'expliquer pourquoi un polluant atmosphérique peut se répandre sur de grandes surfaces, ou encore pourquoi certains parfums envahissent une pièce et disparaissent par la suite.
Représentation du phénomène de la diffusion: un gaz concentré en un endroit (à gauche) se répartit de façon uniforme dans tout l'espace disponible (à droite) lors du phénomène de diffusion.
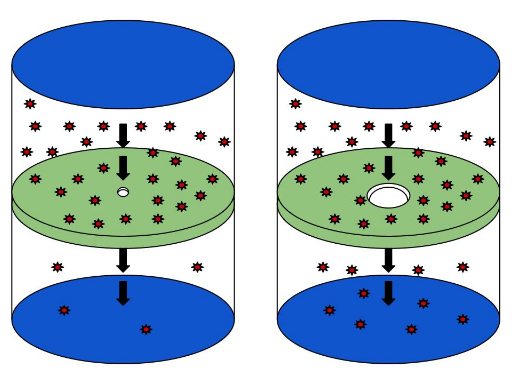
Certains contenants, plutôt que d'être parfaitement hermétiques, ont des parois poreuses, c'est-à-dire des parois dotées de trous minuscules. Les particules de gaz peuvent alors, au hasard des collisions, passer à travers ces petites ouvertures et s'échapper dans l'environnement. On parle alors d'effusion. Un ballon d'hélium qui se dégonfle lentement est un exemple d'effusion. Le dioxygène et le gaz carbonique qui traversent la paroi des capillaires sanguins en est un autre.
L'effusion, qui est le passage de particules de gaz à travers une membrane, se déroule plus rapidement si l'ouverture est grande (à droite) comparativement à une petite ouverture (à gauche).
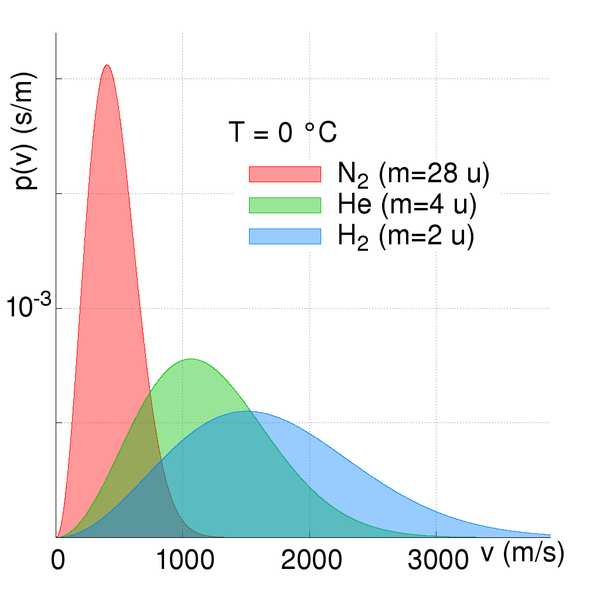
La vitesse d'effusion ou de diffusion des particules n'est pas la même pour tous les gaz. Ce rythme dépend principalement de la masse des particules. En effet, à une température donné, toutes les particules ont la même quantité d'énergie cinétique. Cette énergie dépend de la masse et de la vitesse des particules. Comme des gaz différents sont formés de particules de masses différentes, leur vitesse moyenne sera différente. Ainsi, les particules de masses plus élevées diffusent plus lentement que les particules légères, car elles se déplacent plus lentement.
Courbe de distribution des vitesses en fonction de la masse: un gaz plus lourd tel que le diazote se déplace plus lentement qu'un gaz léger comme le dihydrogène.
La loi de Graham stipule que les vitesses de diffusion, ou d'effusion, de deux gaz aux mêmes conditions de températures et de pression sont inversement proportionnelles à la racine carrée de leurs masses molaires.
En 1840, le chimiste écossais Thomas Graham a posé que, pour des conditions de température et de pression équivalentes, les énergies cinétiques de deux gaz étaient égales. Puisque l'énergie cinétique est fonction de la masse et de la vitesse des particules, il a pu élaborer la loi suivante:
|\displaystyle \frac{Vitesse_{1}}{Vitesse_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}|
où
|Vitesse_{1}|=vitesse de diffusion ou d'effusion du gaz 1 (en m/s ou mL/s)
|Vitesse_{2}|=vitesse de diffusion ou d'effusion du gaz 2 (en m/s ou mL/s)
|M_{1}|=masse molaire du gaz 1 (en g/mol)
|M_{2}|=masse molaire du gaz 2 (en g/mol)
À noter: Dans la loi de Graham, les masses molaires des gaz 1 et 2 pourraient être remplacées par leurs masses en grammes.
Cette loi indique que, dans des conditions de température et de pression identiques, les vitesses de diffusion de deux gaz sont inversement proportionnelles aux racines carrées de leurs masses molaires. Cette loi peut aussi s'appliquer à la vitesse d'effusion des gaz. La loi de Graham est en accord avec la théorie cinétique des gaz, puisque plus les particules d'un gaz sont légères, plus elles se déplacent rapidement. Les particules de gaz plus légères diffusent plus rapidement dans un autre gaz que les particules plus lourdes.
Quelle est la masse molaire d'un gaz inconnu Z qui diffuse à 700 mL/min dans un appareil à diffusion, pendant que le méthane, |CH_{4}|, diffuse à 350 mL/min dans le même appareil?
- Identification des données du problème
|Vitesse_{1}=700 mL/min| pour le gaz inconnu Z
|Vitesse_{2}=350 mL/min| pour le |CH_{4}|
|M_{1}=x| pour le gaz inconnu Z
|M_{2}=16 g/mol| pour le |CH_{4}| - Calcul de la masse molaire
|\displaystyle \frac{Vitesse_{1}}{Vitesse_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}|
|\displaystyle \frac{700 mL/min}{350 mL/min}=\sqrt{\frac{16 g/mol}{x}}|
|x=4 g/mol|
Réponse: La masse molaire du gaz inconnu Z est de 4 g/mol.