When a basic substance is put into aqueous solution, the equilibrium constant takes on a particular form. Scientists have therefore developed a variant of the equilibrium constant to be applied in this situation: the basicity constant. However, an equilibrium reaction can only occur when a weak base dissociates. Strong bases dissociate completely in solution, which constitutes a complete and therefore irreversible reaction.
The strength of an electrolyte, whether acidic or basic, corresponds to the percentage of dissociation of the substance into ions when put into solution.
A strong electrolyte is a solute that dissociates completely in water.
A weak electrolyte is a solute that does not dissociate completely in water.
As stated in the Arrhenius and BrØnsted-Lowry theories, acids and bases are substances that release ions when in aqueous solution. They are therefore electrolytes. However, they do not all undergo electrolytic dissociation to the same degree. This explains the presence of strong and weak electrolytes. Before studying the basicity constant, it is important to distinguish between these substances on the basis of their strength, since only weak electrolytes will be in a state of chemical equilibrium.
An example of a strong electrolyte: sodium hydroxide |(\text{NaOH})|
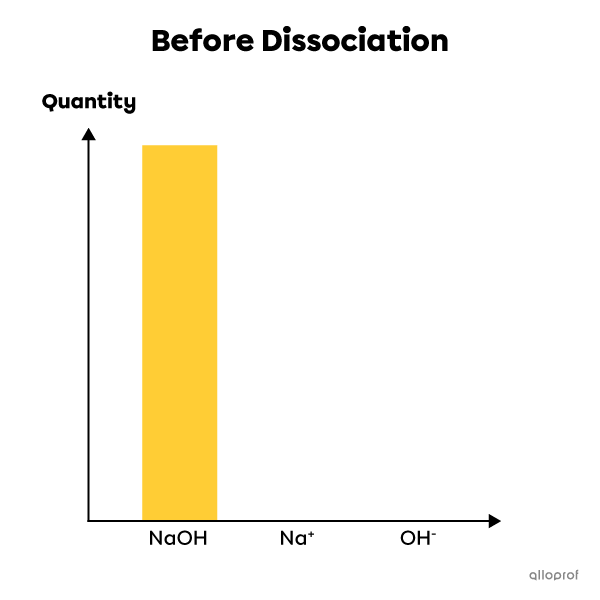
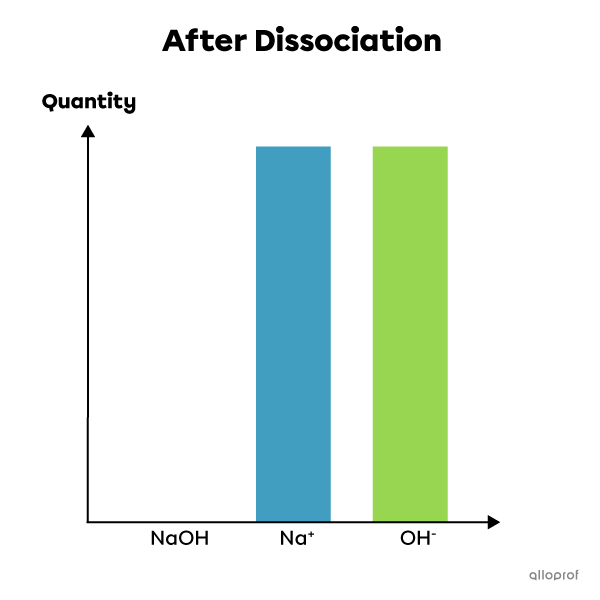
Sodium hydroxide is a strong electrolyte. When dissolved in water, it dissociates completely into ions. Thus, 100% of its molecules dissociate to form ions |\text{Na}^{+}| and |\text{OH}^{-}.| The solution then contains the same percentage of ions after dissociation as there were base molecules before dissociation. It is therefore a complete reaction that cannot be at equilibrium. This chemical reaction is written as follows:
|\text{NaOH}_{\text{(aq)}}^+ \rightarrow \text{Na}^+_{\text{(aq)}}+\text{OH}^-_{\text{(aq)}}|
An example of a weak electrolyte: ammonia |(\text{NH}_3)|

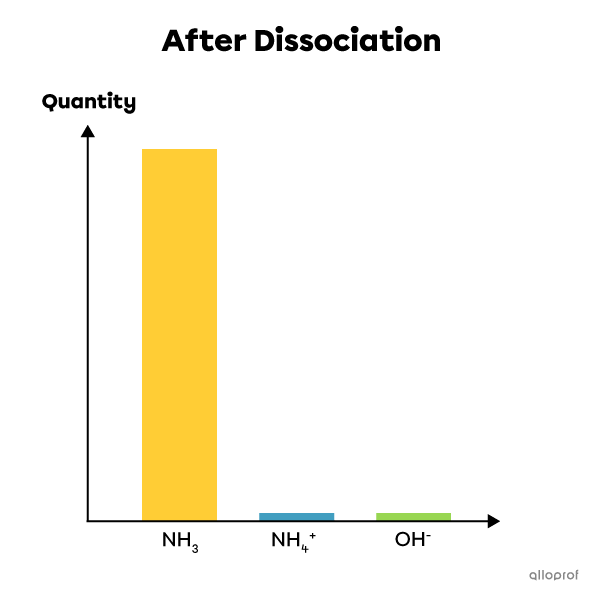
Ammonia is a weak electrolyte. When it is dissolved in water, only some of its molecules dissociate into ions. So most of its molecules remain whole after dissolution, while a very small percentage dissociate and form ions. The solution therefore contains both reactants (the whole molecule) and products (the ions in solution). It is therefore an incomplete and reversible reaction that is at equilibrium. This chemical reaction can be written as follows:
|\text{NH}_{3(\text{aq})}+\text{H}_2\text{O}_{(\text{l})}\leftrightharpoons \text{NH}_{4{(\text{aq})}}^+ +\text{OH}^-_{(\text{aq})}|
Only weak electrolytes can be at equilibrium.
The percentage of molecules that dissociate in an electrolyte can be calculated using the percentage ionisation formula:
|\text {Percentage of ionisation} = \dfrac{[\text{OH}^{-}]}{[\text{B}]}\times 100|
where
|[\text{OH}^{-}]| : concentration of hydroxide ions at equilibrium |(\text {mol/L})|
|[\text{B}]| : concentration of the base before dissolution |(\text {mol/L})|
As well as giving us the percentage ionisation of the electrolyte, this formula allows us to determine the concentration of ions in equilibrium. We can then calculate the basicity constant.
Most bases are weak bases that can reach equilibrium in aqueous solution. At equilibrium, the molecules of the base dissociate at the same rate as the ions formed recombine to reform the molecules of the base. This reaction can be generalised as follows:
|\text{B}_{(\text{aq})} + \text{H}_{2}\text{O}_{(\text{l})} \rightleftharpoons \text{HB}^{+}_{(\text{aq})} + \text{OH}^{-}_{(\text{aq})}|
or :
|\text{B}_{(\text{aq})} \rightleftharpoons \text{B}^{+}_{(\text{aq})} + \text{OH}^{-}_{(\text{aq})}|
The equilibrium constant associated with the ionisation of a base, called the ‘basicity constant’, is then expressed as follows:
|K_{b}=\dfrac{[\text{B}^{+}][\text{OH}^{-}]}{[\text{B}]}|
where
|K_{b}| : basicity constant
|[\text{B}^{+}]| : concentration of the conjugated acid |(\text{mol/L})|
|[\text{OH}^{-}]| : concentration of hydroxide ions in water |(\text{mol/L})|
|[\text{B}]| : concentration of undissociated base |(\text{mol/L})|
The basicity constant |K_{b}| is a variant of the equilibrium constant. It does not include the concentration of water, since water is in the liquid phase. The basicity constant is used to classify bases according to their strength. The higher the constant, the stronger the base.
1. Expression of the basicity constant
The theoretical equation for the constant is used, since the base in solution is not known.
|K_{b}=\displaystyle \frac{[B^{+}][OH^{-}]}{[B]}|2. Calculation of |OH^{-}| ion concentrations
|[H^{+}] = 10^{-pH}|
|[H^{+}] = 10^{-8.2}|
|[H^{+}] = 6.3\times 10^{-9} \text { mol/L}|
|K_{eau} = [H^{+}][OH^{-}]| so
|[OH^{-}] = \displaystyle \frac{1\times 10^{-14}}{6.3\times 10^{-9}}|
|[OH^{-}] = 1.6\times 10^{-6} \text { mol/L}|
3. Table of equilibrium concentrations
| | |B| | |\rightarrow| | |B^+| | |+| | |OH^-| |
| [Initiale] | |\color{red}{0.20}| | |\huge \Rightarrow| | |\color{red}{0}| | |\huge +| | |\color{red}{0}| |
| [Variation] | |(-1.6\times 10^{-6})| | |(+1.6\times 10^{-6})| | |(+1.6\times 10^{-6})| | ||
| [Équilibre] | |0.19| | |1.6\times 10^{-6}| | |\color{red}{1.6\times 10^{-6}}| |
4. Calculation of the basicity constant
|K_{b}=\displaystyle \frac{[1.6\times 10^{-6}][1.6\times 10^{-6}]}{[0.19]}|
|K_{b}=1.35\times 10^{-11}|
The following tools may be useful for calculating |K_{b}|: