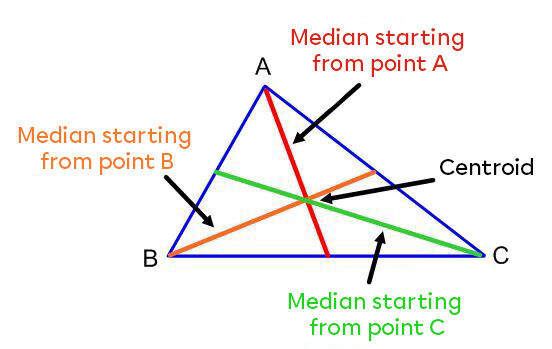
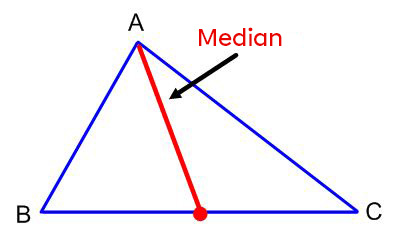
A median is a segment connecting a triangle’s vertex to the middle of the side opposite the vertex.
We can draw a triangle’s median using two methods:
There are three medians in a triangle. The meeting point of the medians is called a triangle’s centroid.
First, draw a segment’s perpendicular bisector and identify the midpoint before constructing the median that comes from the opposite vertex.
We can draw a triangle’s median using a compass and a ruler by following these steps:
-
Open the compass to an opening larger than half of the side opposite the vertex from which the median will start. Keep the same opening for every step of the construction.
-
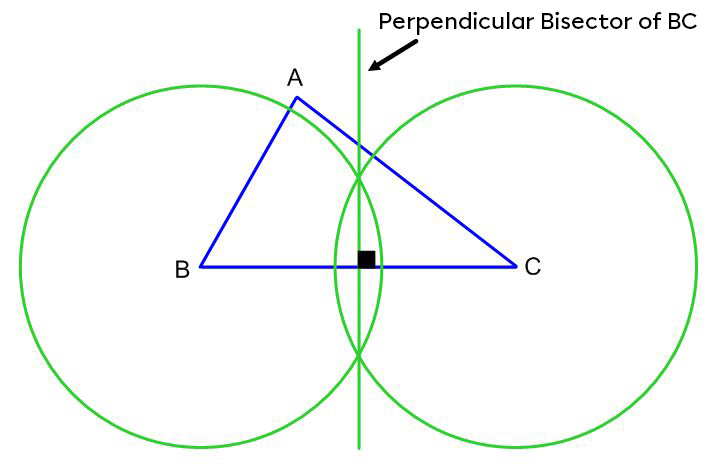
Place the sharp point on one end of side |\overline{BC}| and draw a circle.
-
Repeat step 2 from the other end of side |\overline{BC}.|
-
Using a ruler, draw a straight line connecting the two intersections of the circles. This straight line is the perpendicular bisector of side |\overline{BC}| of the triangle.
-
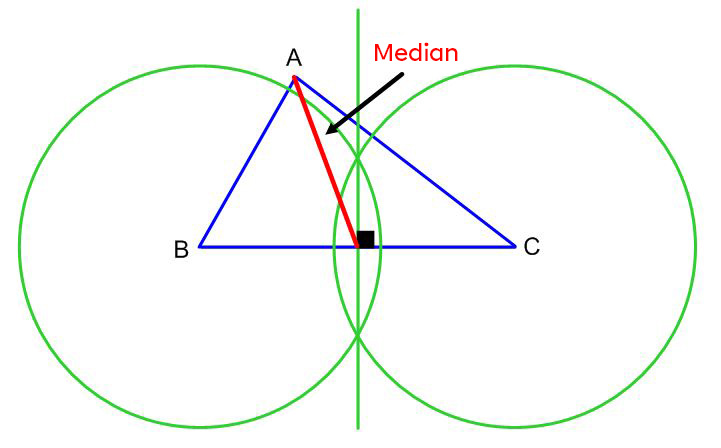
Using a ruler, draw a straight line connecting vertex |A| of the triangle to the intersection point of side |\overline{BC}| and its perpendicular bisector. This straight line is the median of side |\overline{BC}.|
|
|
|
 |
 |
|
Rather than drawing circles, one could simply construct the median by drawing arcs above and below the base of the triangle.
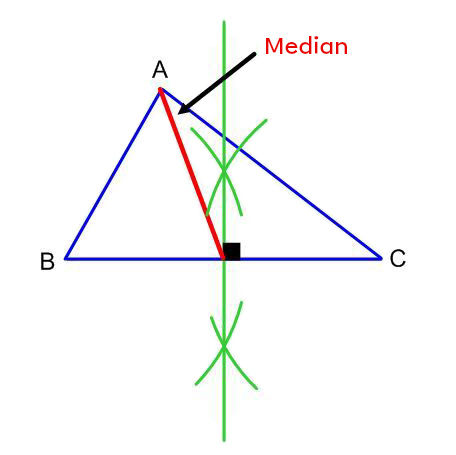
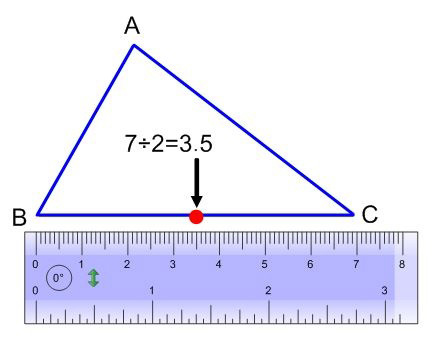
We can use a ruler to draw the a triangle’s median by following these steps:
-
Using a ruler, measure the segment you want to separate into two equal parts.
-
Divide the segment measurement value in half and mark it on the segment.
-
Draw a line segment from vertex A to the point drawn in step 2. This line is the median of the triangle.
|
 |
 |
|