Though they look similar, a line and a straight line do not refer to the same geometric concept.
A line is a continuous set of points which are not necessarily aligned.
A straight line is an infinite number of points which are aligned one next to the other. It is infinite.
In both cases, the points are so close to one another that it is impossible to distinguish them with the naked eye.
Click on Demo to start the video.
Here is a complete list of the different types of lines.
Lines
Straight Lines
Different lines can be combined to compose plane figures.
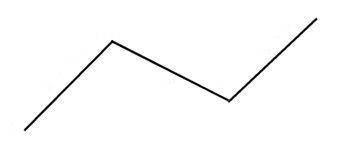
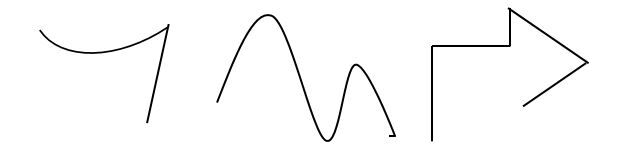
A broken line is formed by a continuous series of several line segments.
Several line segments are joined together from endpoint to endpoint to form a broken line.

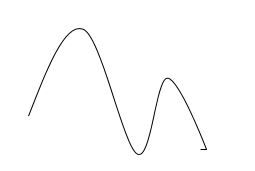
A curved line is a line whose path is continually changing direction.
Curved lines are characterized by curved segments. There are no straight segments in a curved line.

A closed line is a line with ends that meet.
Closed lines can be curved, straight, or both. The important thing to remember is that the end point must be the same as the starting point. There should be no gap.

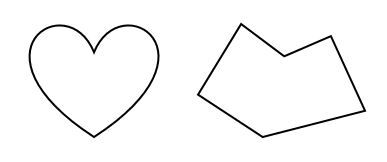
An open line is a line with two ends that do not meet.
Open lines can be curved, straight, or both. The key thing to remember here is that the end point is not the same as the starting point. Therefore, an open line is the opposite of a closed line.
A line is an open line formed by an infinite number of aligned points.
We can name a line with a lowercase letter or two uppercase letters, each corresponding to a point on that line.
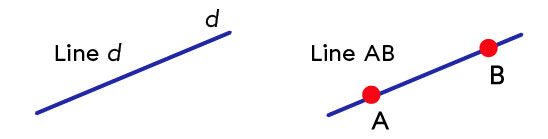
A line has no beginning or end. It continues in both directions to infinity. Therefore, the measurement of a straight line is impossible because it is infinite.
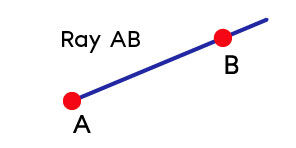
A ray is a section of a straight line that begins at a point called the origin.
Just like a line, a ray continues on in one direction forever and is impossible to measure. Thus, it has no defined dimension.
Point |A| below corresponds to the origin of the ray |AB.|
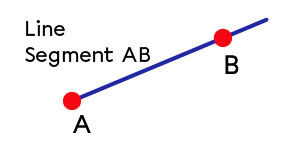
A line segment is a section of a line limited by two endpoints.
It is possible to measure the size of a line segment. The measurement corresponds to the distance between the two endpoints of the line segment.
The segment |\overline{AB}| below is limited by endpoints |A| and |B.|