Content code
m1226
Slug (identifier)
constructing-regular-polygons
Parent content
Constructing Polygons
Grades
Secondary I
Secondary II
Topic
Mathematics
Tags
régulier
polygone régulier
symétrie
centre
axes de symétrie
règle
représenter un polygone
tracer un polygone
dessiner un polygone
axe de symétrie
polygones réguliers
polygones
pentagones
hexagones
Content
Contenu
Corps

Constructing regular polygons requires a ruler, a protractor, and/or a compass. In addition, the various methods proposed below require a good understanding of the concepts of interior angle and central angle.

There are different ways to draw a regular polygon depending on the property referred to.

Links
Type
Anchor
Title
According to Their Central Angles
Anchor
central-angles
Type
Anchor
Title
According to Their Interior Angles
Anchor
interior-angles
Type
Anchor
Title
Drawing Axes of Symmetry...
Anchor
symmetry
Type
Anchor
Title
... of a Regular Polygon with an Even Number of Sides
Anchor
even
Type
Anchor
Title
... of a Regular Polygon with an Odd Number of Sides
Anchor
odd
Title (level 2)
According to their Central Angles
Title slug (identifier)
central-angles
Contenu
Corps

This method makes it possible to construct a regular polygon when the side measurements are not specified. Follow these steps to use this method.

Surtitle
Rule
Content
Corps

  1. Draw a point in the centre of a circle. Open a compass and place the compass tip on that point. Use the compass to draw a circle, making sure to keep the same opening. Tip: The larger the compass opening, the larger the regular polygon.

  2. With a ruler, draw a radius connecting a point on the circle to its centre.

  3. Using the central angle formula, calculate the measurement of each angle at the centre of the regular polygon.

  4. Use a protractor and the circle’s radius to draw an angle in the centre whose measurement is equivalent to the one calculated in step 3. Extend the line to obtain another radius.

  5. Repeat step 4, making sure to proceed from one adjacent angle to another moving clockwise or counterclockwise.

  6. Complete the regular polygon by using a ruler to connect the intersections where each radius meets the circle.

Corps

This procedure can be used to construct almost any type of regular polygon.

Content
Corps

Construct a regular pentagon using a ruler and compass.

  1. Draw a point in the centre of the circle. Open the compass to |4\ \text{cm},| for instance, and place the compass tip on the point. Draw a circle, making sure to keep the same opening. Note:  Larger regular polygons can be built by increasing the compass opening.

  1. Use a ruler to draw a radius connecting a point on the circle and its centre.

  1. Using the central angle formula, calculate the measurement of each angle at the centre of the regular polygon. The pentagon has 5 sides, so each angle in the centre is |72^\circ.| 
    ||\begin{align*}
    \text{Central angle} &= \frac{360^o}{\text{n}} \\ \\
    &= \dfrac {360^\circ}{5} \\ \\
    &= 72^\circ
    \end{align*}||​

  1. Construct a central angle of |72^\circ| using the circle’s radius and the protractor. Extend the line to obtain another radius.

  1. Repeat step 4, making sure to proceed from one adjacent angle to another moving clockwise or counterclockwise.

  1. Using a ruler, connect the intersections where each radius meets the circle to complete the regular polygon. If the steps do not need to be shown, erase the central angles and the circle. Otherwise, keep them.
Title (level 2)
According to their Interior Angles
Title slug (identifier)
interior
Contenu
Corps

The following method can be used to construct a regular polygon when the measurements of its sides are known. To do so, follow these steps.

Surtitle
Rule
Content
Corps

  1. Using a ruler, draw a line segment whose length corresponds to the measurement of the regular polygon’s side. 

  2. Find the measurement of the desired interior angles using the formula for calculating the interior angle of a regular polygon.

  3. Using a protractor, construct an angle at one end of the line segment that is equivalent to the measurement of the interior angle.

  4. Respecting the angle constructed in step 3, draw another line segment whose length is equivalent to the polygon’s side measurement.

  5. At the end of this line segment, use a protractor to construct another angle equivalent to the first one. Then, draw another line segment to form the next side of the regular polygon.

  6. Repeat step 5 until the regular polygon is closed and completed.

Corps

Only a ruler and protractor are needed to construct this polygon.

Content
Corps

Follow these steps to construct a regular hexagon whose sides measure |3\ \text{cm}|.

  1. Use a ruler to draw a line segment whose length corresponds to the measurement of the regular polygon’s side (|3\ \text{cm}|).

  1. Using the formula for calculating the interior angle of a regular polygon, find the measurement of the polygon’s interior angles. Since a hexagon has 6 sides (|n=6|), each interior angle will be |120^\circ.| 
    ||\begin{align*} \text{Interior angle} &= \dfrac{(n -2) \times 180^\circ}{\text{n}}\\​ \\ &= \dfrac{(6-2) \times 180^\circ}{6} \\ \\ &= 120^\circ \end{align*}||

  1. Construct a |120^\circ| angle at one end of the line segment using a protractor.

  1. Using a ruler, and respecting the angle constructed in step 3, draw another line segment whose length is equivalent to the polygon’s side measurement (|3\ \text{cm}|).

  1. At the end of this line segment, use a protractor to construct an angle equivalent to the first (|120^\circ|).

    Then, draw another line segment to form the next side of the regular hexagon (|3\ \text{cm}|).

 

  1. Repeat step 5 until the regular hexagon is closed and completed.
Title (level 2)
Drawing Axes of Symmetry
Title slug (identifier)
symmetry
Contenu
Content
Corps

An axis of symmetry is a line that cuts a figure into two equal parts. Each part overlaps perfectly when the figure is folded along the axis of symmetry.

Corps

In regular polygons, there are as many axes of symmetry as there are sides. Thus, a triangle has 3 axes of symmetry while an octagon has 8.

Content
Corps

Here are the axes of symmetry of the main regular polygons.

Image
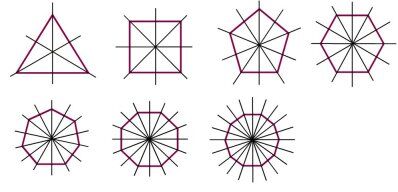
Symmetry
Corps

To construct axes of symmetry in a regular polygon, it is important to consider the number of sides as this will provide the number of axes of symmetry it contains. The best method for constructing the axes of symmetry will differ depending on whether the regular polygon has an even or an odd number of sides.

Surtitle
Rule
Content
Corps

If the regular polygon has an even number of sides (|4, 6, 8, 10...|) there will be an axis of symmetry for each pair of opposite sides. In addition, there will be an axis of symmetry connecting each pair of opposite vertices.

Corps

It is necessary to use a ruler when drawing the axes of symmetry.

Content
Corps

Draw the axes of symmetry of a regular hexagon whose sides measure |4\ \text{cm}.|

  1. Measure one side of a regular hexagon (|4\ \text{cm}|).

  1. Using a ruler, measure half of each side (|2\ \text{cm}|) and mark these midpoints.

  1. Connect the midpoints of each pair of opposite sides to construct the axes of symmetry. Keep using a ruler. The lines must extend beyond the sides of the hexagon.

  1. Connect the opposite vertices of the hexagon. Making sure to go through the centre of the polygon.
Surtitle
Rule
Content
Corps

If the regular polygon has an odd number of sides (|3, 5, 7, 9...|), there will be an axis of symmetry from each vertex connecting to the midpoint of the opposite side.

Corps

Use a ruler when drawing the axes of symmetry.

Content
Corps

Draw the axes of symmetry of a regular pentagon whose sides measure |4\ \text{cm}.|

  1. Measure the side of the regular pentagon (|4\ \text{cm}|).

 

  1. Using a ruler, measure half of each side (|2\ \text{cm}|) and mark these midpoints.

  1. Connect each vertex with the midpoints of the opposite sides to build the axes of symmetry. Keep using a ruler. The lines should extend beyond, and be perpendicular to, the sides of the pentagon.
Remove audio playback
No