Polygons are often classified in reference to the measurements of their sides, angles, and diagonals. In some cases, the side and angle measurements of a polygon will be identical.
A regular polygon is a polygon where all sides and all interior angles have the same measurement.
Note: The more sides a regular polygon has, the more it resembles a circle.
It is possible to find the names of the main regular polygons according to their number of sides, by consulting the concept sheet on the classification of polygons.
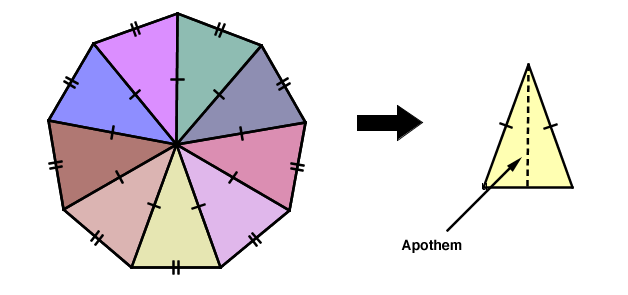
The apothem is a perpendicular line segment drawn from the centre of a regular polygon to the midpoint of any of its sides.
To solve problems that involve these concepts, it may be useful to use the Pythagorean Theorem.
Note that there are as many apothems as there are sides in a regular polygon.
Every regular polygon can be decomposed into triangles.
The triangles formed through decomposition are isosceles triangles whose height corresponds to the regular polygon’s apothem.
The triangles are indeed isosceles because the vertices of a regular polygon are located at an equal distance from the centre.
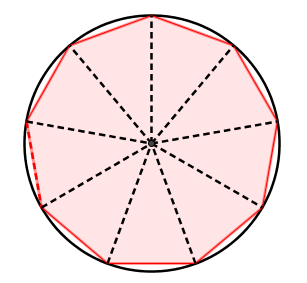
Polygon inscribed in a circle
To illustrate that these triangles are indeed isosceles, it is possible to inscribe a regular polygon in a circle. Notice that the sides of the triangles represented by the dotted lines are, in fact, the radii of the circle.
The radii of a circle are always equal, thus all of the triangles are isosceles. Moreover, since the base of these triangles corresponds to the sides of the regular polygon, we can determine that all of the triangles are congruent (isometric).
Since they are isosceles and congruent, the angle measurements of these triangles can be determined.
The central angle of a regular polygon is the angle formed by connecting the centre of a regular polygon to a pair of consecutive vertices. The central angle can also be seen as the angle formed at the apex of one of the isosceles triangles that make up a regular polygon.
||\begin{gather}\text{Measure of the central angle}=\dfrac{360^\circ}{n}\\\text{where}\\ n:\text{number of sides of the regular polygon}\end{gather}||
Grouping together all of the angles at the centre of a regular polygon results in a full angle of |360^\circ.| Since the isosceles triangles that compose a regular polygon are congruent, it can be determined that each central angle has the same measurement.
What is the measure of the central angle of the following regular decagon?
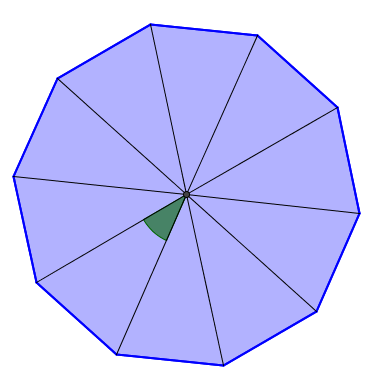
-
Identify the full angle formed by the angles at the centre
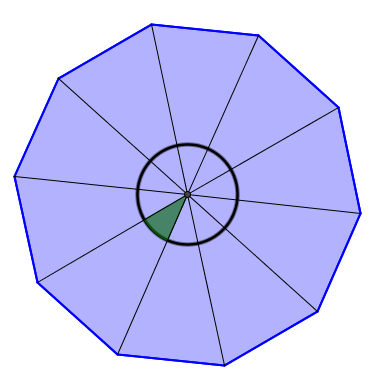
-
Apply the formula
||\begin{align*}
\color{green}{\text{Measurement of the central angle}} &= \displaystyle \frac{360^\circ}{n} \\
&= \displaystyle \frac{360^\circ}{10} \\
&= \color{green}{36^\circ}
\end{align*}||
Since the measurement of one of the angles of the isosceles triangles (of which the regular polygon is composed) is known, the other two angle measurements can be found. To find them, use the following two characteristics of isosceles triangles:
-
The sum of the interior angles of a triangle is |180^\circ.|
-
An isosceles triangle has two congruent angles.
Given that the polygon below is regular, what are the angle measurements of the triangle?
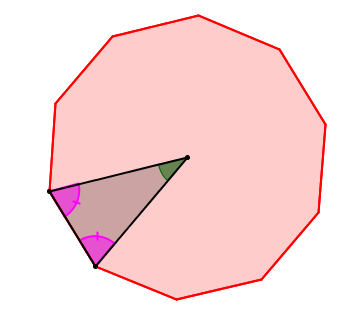
-
Find the measurement of the central angle
||\begin{align*}
\color{green}{\text{measure of central angle}} &= \displaystyle \frac{360^\circ}{10} \\
&= \color{green}{36^\circ}
\end{align*}|| -
Determine the other two angles’ measurements
Since it is an isosceles triangle, ||\begin{align*}
180^\circ &= 2 \times\color{fuchsia}{\text{angle measure}} + 1 \times \color{green}{\text{measure of central angle}}\\
180^\circ &= 2 \times \color{fuchsia}{\text{angle measure}} + 1 \times \color{green}{36^\circ}\\
144^\circ &= 2 \times\color{fuchsia}{\text{angle measure}}\\
\color{fuchsia}{72^\circ} &= \color{fuchsia}{\text{angle measure}}
\end{align*}||
We equally could have found the measure of an interior angle of the polygon and have divided it by two. Since the triangles that compose a regular polygon are isosceles and congruent, this approach is equally valid.
Amongst all the regular polygons, only the hexagon can be decomposed into equilateral triangles.
The Regular Hexagon
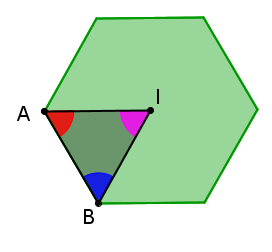
To demonstrate that |\triangle{ABI}| is indeed an equilateral triangle, determine the measure of each of the angles.
-
Find the measure of |\color{fuchsia}{\angle AIB}| (central angle)
||\begin{align*}
\color{fuchsia}{m\angle{AIB}} &= \displaystyle \frac{360^\circ}{6} \\
&= \color{fuchsia}{60^\circ}
\end{align*}|| -
Find the measure of |\color{red}{\angle IAB}| (half of an interior angle)
||\begin{align*}
\color{red}{m\angle IAB} &= \displaystyle \frac{1}{2}\left( \frac{(n-2)\times 180^\circ}{n}\right) \\
&= \displaystyle \frac{1}{2}\left(\frac{(6-2)\times 180^\circ}{6}\right) \\
&= 60^\circ
\end{align*}|| -
Find the measure of |\color{blue}{\angle ABI}|
Since the sum of the interior angles of a triangle is |180^\circ|, use the following formula :
||\begin{align*}
180^\circ &= \color{fuchsia}{m\angle AIB} + \color{red}{m\angle IAB} + \color{blue}{m\angle ABI}\\
180 ^\circ &= \color{fuchsia}{60^\circ} + \color{red}{60^\circ} + \color{blue}{m\angle ABI} \\
60^\circ &= \color{blue}{m\angle ABI}
\end{align*}|| -
Interpret the answer
Since the three angles have a measure |60^\circ,| then the triangle is equiangular, and therefore, equilateral.
To find the measure of a single interior angle of a regular polygon, divide the sum of the interior angle measurements by the number of angles it contains.
||\begin{align}\text{Measure of an Interior Angle}&=\dfrac{\text{sum of the interior angles}}{\text{number of sides of the polygon}}\\&=\dfrac{(n - 2)\times180^\circ}{n}\end{align}||
The following is the measure of an interior angle of a regular heptagon.
||\begin{align} \text{Measure of an Interior Angle} &= \displaystyle \frac{(n-2) \times 180^\circ}{n} \\
&= \frac{(7-2) \times 180^\circ}{7} \\
&\approx 128.57^\circ \end{align}||
There are other ways to calculate the measure of an interior angle of a regular polygon. For example, by finding the measure of the two congruent angles at the base of the isosceles triangle (which comes from decomposing the polygon into triangles), finding the interior angle’s measurement is made easy. The example below demonstrates this.
In this situation, all of the measures of the isosceles triangle |OAB| have been calculated. Notice that angle |\color{#ec0000}{ABC}| is formed by angles |\color{#ff55c3}{\angle{ABO}}| and |\color{#ff55c3}{\angle{OBC}},| which are congruent.
||\begin{align}\color{#ec0000}{\text{Measure of an Interior Angle}}&=2\times\color{#ff55c3}{m\angle{ABO}}\\&=2\times 72^\circ\\&=144^\circ\end{align}||
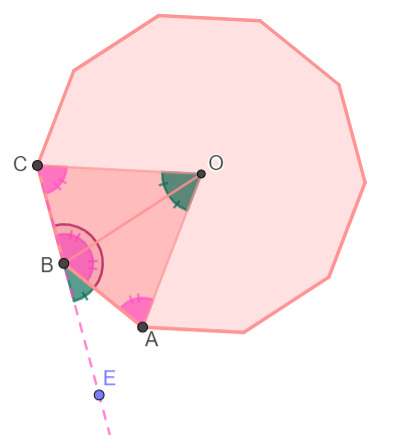
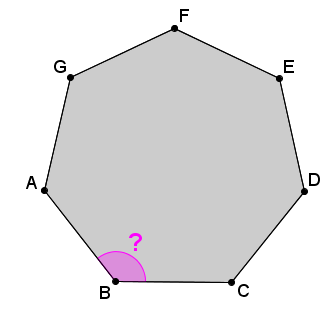
An exterior angle of a polygon is an angle formed between one side of the polygon and the extension of the adjacent side.
In the following figure, angle |ABE| is an exterior angle.
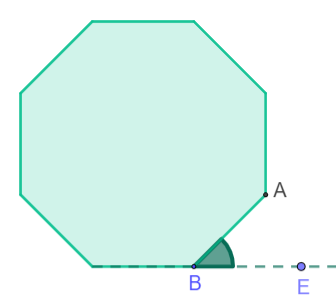
A polygon has as many exterior angles as sides.
The sum of the exterior angles of any convex polygon is always 360°. The following animation shows the nine exterior angles of an enneagon (nonagon). Press the "play" button at the bottom left to start the animation.
To find the measure of a single exterior angle of a regular polygon, divide the sum of the polygon’s angles (which is always |360^\circ|) by the number of angles it contains (same as the number of sides).
||\begin{align}\text{Measurement of an Exterior Angle}&=\dfrac{360^\circ}{\text{number of sides of the polygon}}\\&=\dfrac{360^\circ}{n}\end{align}||
Here is the measure of an exterior angle of a regular pentagon.
||\begin{align}\text{Measure of an Exterior Angle}&=\dfrac{360^\circ}{n}\\
&=\dfrac{360^\circ}{5}\\
&=72^\circ\end{align}||
The measure of an exterior angle can also be calculated from the measure of the interior angle.
The interior angle and exterior angle of a polygon are supplementary. Using this information, the following two formulas are obtained:
||\begin{gather}\text{Measure of Exterior Angle}=180^\circ-\text{Measure of Interior Angle}\\\\\text{and}\\\\\text{Measure of Interior Angle}=180^\circ-\text{Measure of Exterior Angle}\end{gather}||
Consider the following regular polygon:
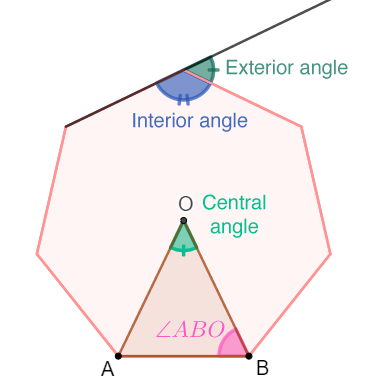
In the following table, we find how to calculate the measure of angles in regular polygons when given other measurements. The table should be read as follows: the top row indicates the given measurement, while the first column specifies the missing measurement. In all the formulas, the variable |n| represents the number of sides of the regular polygon.
|
Given measurement |\rightarrow| |
Central angle |(\color{#05BF8E}{m\angle centre})| |
Exterior angle |(\color{#076C56}{m\angle ext})| |
Interior angle |(\color{#2753B6}{m\angle int})| |
Two congruent angles of the isosceles triangle |(\color{#FF55C3}{m\angle ABO})| |
Sum of the interior angles |(\sum \angle int)| |
|
|\color{#05BF8E}{m\angle centre}=| |
|
|\color{#076C56}{m\angle ext}| |
|180°-\color{#2753B6}{m\angle int}| |
|180°-2(\color{#FF55C3}{m\angleABO})| |
|180°-\dfrac{\sum \angle int}{n}| |
|
|\color{#076C56}{m\angle ext}=| |
|\color{#05BF8E}{m\angle centre}| |
|
|180°-\color{#2753B6}{m\angle int}| |
|180°-2 (\color{#FF55C3}{m\angleABO})| |
|180°-\dfrac{\sum \angle int}{n}| |
|
|\color{#2753B6}{m\angle int}=| |
|180°-\color{#05BF8E}{m\angle centre}| |
|180°-\color{#076C56}{m\angle ext}| |
|
|2 (\color{#FF55C3}{m\angleABO})| |
|\dfrac{\sum \angle int}{n}| |
|
|\color{#FF55C3}{m\angleABO}=| |
|\dfrac{180°-\color{#05BF8E}{m\angle centre}}{2}| |
|\dfrac{180°-\color{#076C56}{m\angle ext}}{2}| |
|\dfrac{\color{#2753B6}{m\angle int}}{2}| |
|
|\dfrac{\sum \angle int}{n}\div 2| |
|
|\sum \angle int=| |
|n (180°-\color{#05BF8E}{m\angle centre})| |
|n(180°-\color{#076C56}{m\angle ext})| |
|n (\color{#2753B6}{m\angle int})| |
|n \big(2(\color{#FF55C3}{m\angleABO})\big)| | |
The following interactive animation shows the central, interior, and exterior angles of regular polygons with 3 to 15 sides.
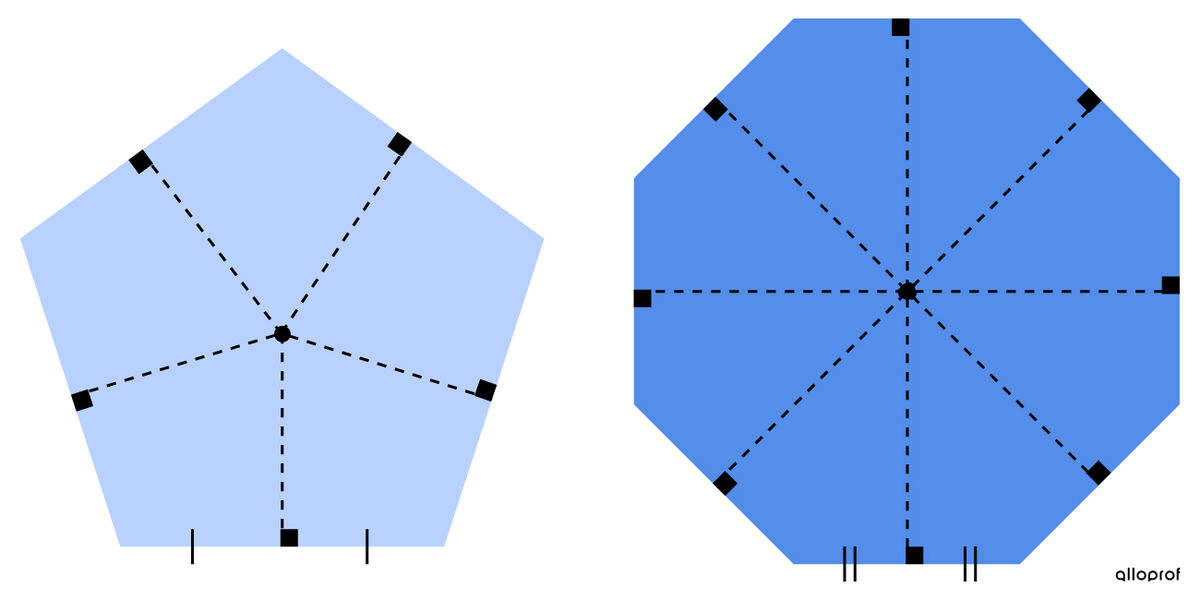
Since the measures of its angles and sides are congruent, a regular polygon has multiple axes of symmetry that can be drawn.
A regular polygon has as many axes of symmetry as there are sides. Thus, an equilateral triangle has three axes of symmetry and a regular hexagon has six.
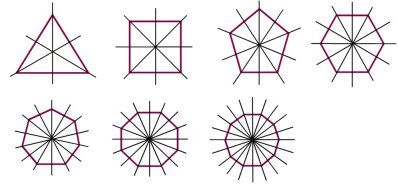
As a reference point for drawing the lines of symmetry, rely on the vertices of the polygon and the midpoint of each sides.
