La construction de polygones réguliers nécessitent l’utilisation d’une règle, d’un rapporteur d’angles ou d’un compas. De plus, ces méthodes requièrent une bonne compréhension des notions d'angle intérieur et d'angle au centre.
Il existe différentes façons de dessiner un polygone régulier selon la propriété à laquelle on fait référence :
Cette méthode permet de construire un polygone régulier lorsque la mesure des côtés n’est pas précisée. Pour ce faire, il s’agit de suivre les étapes suivantes :
-
Dessiner un point qui sera le centre d'un cercle. Ouvrir le compas et placer la pointe sèche du compas sur ce point. Tracer un cercle avec le compas en s’assurant de maintenir la même ouverture. Plus l'ouverture du compas sera grande, plus le polygone régulier construit le sera aussi.
-
À l’aide de la règle, tracer un rayon en reliant un point du cercle et son centre.
-
À l’aide de la formule de l’angle au centre, calculer la mesure de chaque angle au centre du polygone régulier à construire.
-
À l’aide du rapporteur d’angles et du rayon du cercle, construire un angle au centre dont la mesure équivaut à celle calculée à l’étape 3. Prolonger le trait de façon à obtenir un autre rayon.
-
Répéter l'étape 4 en s’assurant de procéder d’un angle adjacent à l’autre dans le sens horaire ou antihoraire.
-
À l’aide de la règle, relier chaque jonction des rayons avec le cercle de manière à former le polygone régulier.
Étant donné les propriétés des polygones réguliers, on peut appliquer cette procédure pour construire presque tous les polygones réguliers.
En utilisant ta règle et ton compas, construis un pentagone régulier.
|
1. Dessiner un point qui sera le centre du cercle. Ouvrir le compas à 4 cm, par exemple, et placer la pointe sèche du compas sur le point. Tracer un cercle en s’assurant de maintenir la même ouverture (Il est possible de construire un polygone régulier plus grand en augmentant l’ouverture du compas). |
2. À l’aide de la règle, tracer un rayon en reliant un point du cercle et son centre. |
|
3. À l’aide de la formule de l’angle au centre, calculer la mesure de chaque angle au centre du polygone régulier. Comme le pentagone compte 5 côtés, chaque angle au centre vaut 72o.||\begin{align*} |
4. À l’aide du rapporteur d’angles et du rayon du cercle, construire un angle au centre de 72o. Prolonger le trait de façon à obtenir un autre rayon. |
|
5. Répéter l'étape 4 en s’assurant de procéder d’un angle adjacent à l’autre dans le sens horaire ou antihoraire. |
6. À l’aide de la règle, relier chaque jonction des rayons avec le cercle de manière à former le polygone régulier. Effacer les angles au centre et le cercle si les traces de la démarche ne sont pas demandées. Sinon, les conserver comme traces de la démarche. |
Cette méthode permet de construire un polygone régulier lorsque la mesure des côtés est précisée. Pour ce faire, il s’agit de suivre les étapes suivantes :
-
À l’aide de la règle, tracer un segment dont la longueur correspondant à la mesure de côté du polygone régulier.
-
À l’aide de la formule de l’angle intérieur d’un polygone régulier, calculer la mesure des angles intérieurs du polygone désiré.
-
À l'une des extrémité du segment initial, construire un angle qui correspond à la mesure de l’angle intérieur du polygone régulier désiré en utilisant le rapporteur d'angles.
-
En utilisant la règle et en respectant l'angle construit à l'étape 3, tracer un autre segment dont la longueur correspond à la mesure de côté du polygone régulier.
-
À l’extrémité de ce segment, construire un autre angle équivalent au premier en utilisant le rapporteur d’angles. Tracer d'un segment un autre côté du polygone régulier.
-
Répéter l’étape 5 jusqu’à ce que le polygone régulier soit fermé et, ainsi, complété.
Pour cette construction, seuls la règle et le rapporteur d'angles sont nécessaires.
Supposons que l’on veuille construire un hexagone régulier de |3\:\text{cm}| de côté. Il s’agit de suivre les étapes suivantes:
|
1. À l’aide de la règle, tracer un segment dont la longueur correspondant à la mesure de côté du polygone régulier. (3 cm). |
2. À l’aide de la formule de l'angle intérieur d’un polygone régulier, calculer la mesure des angles intérieurs du polygone désiré. Comme l'hexagone compte 6 côtés (|n=6|), chaque angle intérieur vaudra 120o. ||\begin{align*} \text{angle intérieur} &= \frac{(n -2) \times 180^o}{\text{n}}\\ \\ &= \frac{(6-2) \times 180^o}{6} \\ \\ &= 120^o \end{align*}|| |
|
3. À l'une des extrémité du segment initial, construire un angle de 120o en utilisant le rapporteur d'angles. |
4. En utilisant la règle et en respectant l'angle construit à l'étape 3, tracer un autre segment dont la longueur correspond à la mesure de côté du polygone régulier. (3 cm). |
|
5. À l’extrémité de ce segment, construire un angle équivalent au premier (120o) en utilisant le rapporteur d'angles. Tracer d'un segment un autre côté de l'hexagone régulier
|
6. Répéter l’étape 5 jusqu’à ce que l'hexagone régulier soit fermé et, ainsi, complété. |
Un axe de symétrie est une droite qui coupe une figure en deux parties égales. L’une des deux parties se superposera parfaitement sur l'autre par pliage le long d'un axe de symétrie.
Dans les polygones réguliers, il y a autant d’axes de symétrie que de côtés. Ainsi, un triangle possède 3 axes de symétrie tandis qu'un octogone en possède 8.
Voici, par exemple, les axes de symétrie des principaux polygones réguliers.
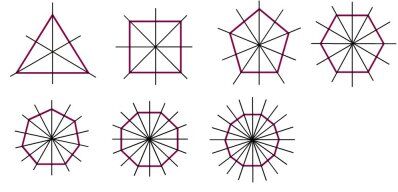
Afin de pouvoir construire les axes de symétrie d'un polygone régulier, il est important de prendre en considération le nombre de côtés et donc, le nombre d'axes de symétrie qu'il contient. En effet, la méthode différera si le polygone régulier possède un nombre pair ou impair de côtés. D'un polygone régulier avec un nombre pair de côtés
Si le polygone régulier possède un nombre pair de côtés (4, 6, 8, 10, ...), il y aura un axe de symétrie pour chaque paire de côtés opposés. De plus, il y aura un axe de symétrie reliant chaque paire de sommets opposés.
Par ailleurs, il est nécessaire d'utiliser la règle tout au long du traçage des axes de symétrie.
Trace les axes de symétrie d'un hexagone régulier de |4\:\text{cm}| de côté.
|
1. Mesurer le côté de l'hexagone régulier (4 cm).
|
2. À l'aide de la règle, mesurer la moitié de chaque segment de l'hexagone régulier (2cm) et marquer le point milieu de chaque segment.
|
|
3. À l'aide de la règle, relier les marques de chaque paire de côtés opposés afin de construire les axes de symétrie. Les traits doivent dépasser les côtés de l'hexagone.
|
4. À l'aide de la règle, relier les sommets opposés de l'hexagone en prenant soin
|
Si le polygone régulier possède un nombre impair de côtés (3, 5, 7, 9, ...), il y aura un axe de symétrie à partir de chaque sommet qui reliera le centre du côté opposé.
Comme pour tout traçage d'axes de symétrie, il est nécessaire d'utiliser la règle.
Trace les axes de symétrie d'un pentagone régulier de |4\:\text{cm}| de côté.
|
1. Mesurer le côté du pentagone régulier (4 cm).
|
2. À l'aide de la règle, mesurer la moitié de chaque côté (2 cm) du pentagone régulier et marquer le point milieu.
|
|
3. À l'aide de la règle, relier chaque sommet et la marque sur le point milieu de son côté opposé afin de construire les axes de symétrie. Ces traits devraient dépasser de par et d'autre du pentagone et être perpendiculaires au côté.
|
|