Factoring is the process of writing out an algebraic expression as a product of factors.
Generally speaking, factoring simplifies an algebraic expression in order to make it easier to solve. The factors obtained from factoring are polynomials of a same or lesser degree than the starting polynomial.
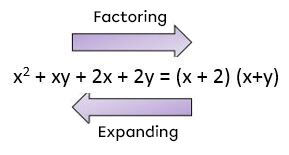
The opposite of factorization is the expansion of an algebraic expression.
Expressions can be factored using different methods:
The steps to follow when factoring a polynomial depend on the number of terms the expression contains. In general, always ensure that the polynomial expression is factored as much as possible. It is possible that more than one method of factoring can be used for the same polynomial.
Situation: Binomial
When the expression being factored is a binomial, follow these steps:
-
Factor out a common factor if possible.
-
If there is a subtraction sign between the two terms of the binomial, see if it is possible to perform a difference of squares.
Situation: A trinomial in the form of |ax^2+bx+c|
When the expression being factored is a trinomial, follow these steps:
-
Factor out a common factor if possible.
-
If the values of |a| and |c| are square roots, check if the trinomial is a perfect square.
-
If the trinomial is not a perfect square, see if it is possible to use the product-sum technique. This method is useful when |a|, |b|, and |c| are whole numbers.
-
If the trinomial is neither a perfect square, nor factorable with the product-sum method, the method of completing the square can be used. This method can always be used as long as the trinomial can be factored.
Before attempting to factor a trinomial in the form of |ax^2+bx+c|, it is useful to calculate the discriminant. The discriminant (symbolised |\Delta|) of a trinomial in the form |ax^2+bx+c| is equal to the value of the expression |b^2-4ac| .
When the value of the discriminant is negative, the trinomial cannot be factored.
Here is an example:
Calculate the discriminant of the trinomial |2x^2-4x+7|.
In this trinomial, |a=2|, |b=-4| and |c=7|. We can now calculate the discriminant:
||\begin{align}\Delta&=b^2-4ac\\ & = (-4)^2-4 (2)(7)\\ &=16-56\\ &=-40\end{align}||
As the discriminant is negative, the trinomial |2x^2-4x+7| is not factorable.
Situation: The number of terms is greater than 3
When the expression being factored contains more than 3 terms, follow these steps:
-
Check if it is possible to factor out a common factor.
-
Check if it is possible to factor by grouping.