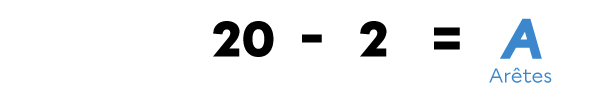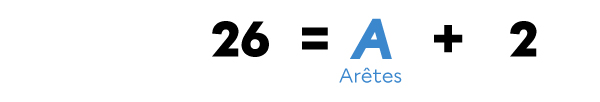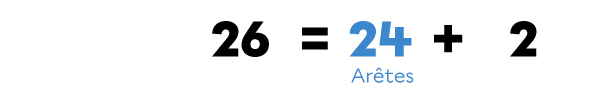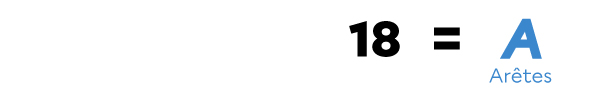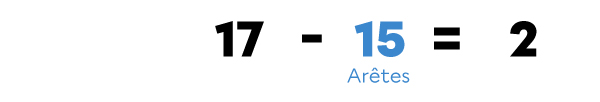La relation d'Euler | Primaire

Voici trois formules qui te permettent d’établir la relation d’Euler. Tu obtiens les mêmes résultats en utilisant l'une ou l'autre de ces formules.

Pour déterminer le nombre d’arêtes d’un polyèdre convexe à l’aide de la formule F + S - 2 = A, je dois suivre les étapes suivantes :

1. J’écris la formule d’Euler en remplaçant le F par le nombre de faces et le S par le nombre de sommets du polyèdre convexe.

2. J’additionne le nombre de faces et le nombre de sommets, puis je réécris l’équation.

3. Je soustrais 2 à la somme obtenue à l’étape 2.

Combien d’arêtes a un polyèdre convexe de 8 faces et 12 sommets?

J’écris la formule d’Euler en remplaçant le F par le nombre de faces et le S par le nombre de sommets du polyèdre convexe. Je remplace le F par 8, car le polyèdre a 8 faces. Je remplace le S par 12, car le polyèdre a 12 sommets.
J’additionne le nombre de faces et le nombre de sommets, puis je réécris l’équation. 8 + 12 = 20
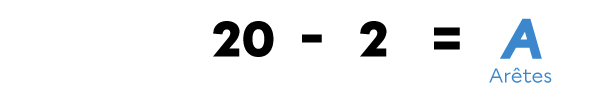Je soustrais 2 à la somme obtenue à l’étape 2. 20 - 2 = 18

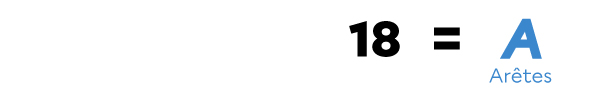
Un polyèdre convexe de 8 faces et 12 sommets a 18 arêtes.

Pour déterminer le nombre d’arêtes d’un polyèdre convexe à l’aide de la formule F + S - A = 2, je dois suivre les étapes suivantes :

1. J’écris la formule d’Euler en remplaçant le F par le nombre de faces et le S par le nombre de sommets du polyèdre convexe.

2. J’additionne le nombre de faces et le nombre de sommets, puis je réécris l’équation.

3. Je trouve le terme manquant (A) dans la soustraction.

Combien d’arêtes a un polyèdre convexe de 7 faces et 10 sommets?

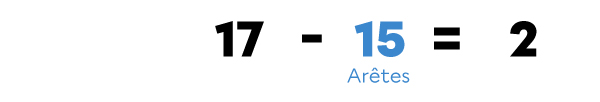
Un polyèdre convexe de 7 faces et 10 sommets a 15 arêtes.

Pour déterminer le nombre d’arêtes d’un polyèdre convexe à l’aide de la formule F + S = A + 2, je dois suivre les étapes suivantes : 

1. J’écris la formule d’Euler en remplaçant le F par le nombre de faces et le S par le nombre de sommets du polyèdre convexe.

2. J’additionne le nombre de faces et le nombre de sommets, puis je réécris l’équation.

3. Je trouve le terme manquant (A) dans l’addition.

Combien d’arêtes a un polyèdre convexe de 10 faces et 16 sommets?

J’écris la formule d’Euler en remplaçant le F par le nombre de faces et le S par le nombre de sommets du polyèdre convexe. Je remplace le F par 10, car le polyèdre a 10 faces. Je remplace le S par 16, car le polyèdre a 16 sommets.
J’additionne le nombre de faces et le nombre de sommets, puis je réécris l’équation. 10 + 16 = 26
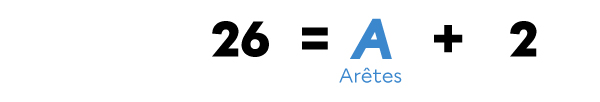Je trouve le terme manquant (A) dans l’addition. Pour savoir comment faire, je peux lire la fiche Trouver un terme manquant dans une addition. 26 - 2 = 24

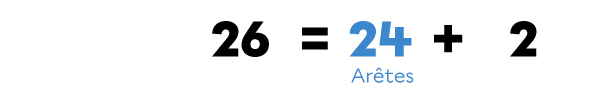 Un polyèdre convexe de 10 faces et 16 sommets a 24 arêtes.

À l’aide de cette formule, tu peux aussi trouver le nombre de faces et de sommets d’un polyèdre. 

Pour trouver le nombre de faces, tu dois connaitre le nombre de sommets et d’arêtes.

Exemple :

Combien de faces a un polyèdre de 6 sommets et 9 arêtes?

Pour trouver le nombre de sommets, tu dois connaitre le nombre de faces et d’arêtes.

Exemple : 

Combien de sommets a un polyèdre de 5 faces et 9 arêtes?