In some situations, it may be useful to convert a fraction into a decimal number or vice versa. The following concept sheet suggests methods to perform these conversions successfully.
A fraction can be seen as a division that has not yet been carried out. Thus, it can be converted to decimal form by simply performing the division represented by the fraction.
-
Divide the numerator of the fraction by the denominator.
-
Write the result of the division.
Express |\displaystyle \frac{3}{4}| as a decimal number.
-
Divide the fraction’s numerator by the denominator.
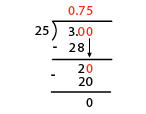
-
Write the result of the division.
The result is | \frac{3}{4}=0.75|.
Express |\displaystyle \frac{2}{25}| as a decimal number.
-
Divide the fraction’s numerator by the denominator.

-
Write the result of the division.
The result is |\displaystyle \frac{2}{25}=0.08|.
Some fractions cannot be written as decimals.
Dividing the numerator by the denominator may not result in a decimal number, but in a periodic number.
For example, the following |\frac{1}{3}=0.33333...=0.\overline{3}|.
To learn how to convert a fraction to a periodic number and vice versa, consult the following concept sheet.
It is possible to express a decimal number as a fraction, as follows.
-
Identify the number of decimal places after the decimal point to determine the denominator to use.
|
Number of decimal places |
Denominator |
|
|1| |
|10| |
|
|2| |
|100| |
|
|3| |
|1000| |
|
... |
... |
-
Write a fraction where the numerator is the decimal number without the decimal point and the denominator is the one chosen in step 1.
-
Simplify the fraction if necessary.
A decimal number can simply be read to express it as a fraction.
For example, the number |0.2| reads as: “two tenths”.
Therefore, the fraction representing the number is |\displaystyle \frac{2}{10}|. The fraction also reads "two tenths".
The final step is to simplify the fraction!
Express |0.54| as a simplified fraction.
-
Identify the number of decimal places after the decimal point to determine the denominator to use.
Note that there are two digits after the decimal point in |0.54|. The number |100| will be used as the denominator. -
Write a fraction where the numerator is the decimal number without the decimal point and the denominator is the one chosen in step 1.
||\displaystyle 0.54=\frac{54}{100}|| -
Simplify the fraction if necessary.
||\displaystyle \frac{54\color{green}{\div 2}}{100\color{green}{\div 2}}=\frac{27}{50}||Thus, |\displaystyle 0.54=\frac{27}{50}|.
Express |0.333| as a simplified fraction.
-
Identify the number of decimal places after the decimal point to determine which denominator to use.
Note that there are three digits after the decimal point in |0.333|. The number |\small 1000| will be used as the denominator. -
Write a fraction where the numerator is the decimal number without the decimal point and the denominator is the one chosen in step 1.
||\displaystyle 0.333=\frac{333}{1000}|| -
Simplify the fraction if necessary.
The fraction cannot be simplified further.
Thus, the result is |\displaystyle 0.333=\frac{333}{1000}|.