Dans certaines situations, il peut être utile de passer d'une fraction à un nombre décimal ou l'inverse. La fiche suivante traite des méthodes à utiliser pour effectuer ces passages avec succès.
Puisqu'une fraction peut être vue comme une division non effectuée, on peut passer à la forme décimale tout simplement en effectuant la division représentée par la fraction.
1. Effectuer la division du numérateur de la fraction par le dénominateur.
2. Écrire le résultat de la division.
Exprime |\displaystyle \frac{3}{4}| en nombre décimal.
1. Effectuer la division du numérateur de la fraction par le dénominateur.
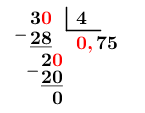
2. Écrire le résultat de la division.
On a donc | \frac{3}{4}=0,75|.
Exprime |\displaystyle \frac{2}{25}| en nombre décimal.
1. Effectuer la division du numérateur de la fraction par le dénominateur.
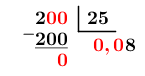
2. Écrire le résultat de la division.
On a donc |\displaystyle \frac{2}{25}=0,08|.
Certaines fractions ne peuvent pas s'écrire en nombres décimaux.
Il se peut que la division du numérateur par le dénominateur ne donne pas un nombre décimal, mais bien un nombre périodique.
Prenons par exemple |\frac{1}{3}=0,33333...=0,\overline{3}|.
Pour savoir comment passer d'une fraction à un nombre périodique et l'inverse, visite la fiche suivante.
Il est possible d'exprimer un nombre décimal en fraction de la façon suivante.
1. Observer le nombre de chiffres après la virgule du nombre décimal pour déterminer le dénominateur à utiliser.
| Nombre de chiffres après la virgule | Dénominateur |
| |1| | |10| |
| |2| | |100| |
| |3| | |1000| |
| ... | ... |
2. Écrire une fraction dont le numérateur est le nombre décimal sans la virgule et dont le dénominateur est celui choisi à l'étape 1.
3. Simplifier la fraction au besoin.
On peut tout simplement lire un nombre décimal pour l'exprimer en fraction.
Prenons le nombre |0,2|. Ce nombre se lit comme ceci : «deux dixièmes».
La fraction représentant ce nombre est donc |\displaystyle \frac{2}{10}|. Cette fraction se lit aussi «deux dixièmes».
Il ne reste plus qu'à simplifier la fraction !
Exprime |0,54| en fraction irréductible.
1.Observer le nombre de chiffres après la virgule du nombre décimal pour déterminer le dénominateur à utiliser.
On remarque qu'il y a deux chiffres après la virgule dans |0,54|. On utilisera le nombre |100| comme dénominateur.
2.Écrire une fraction dont le numérateur est le nombre décimal sans la virgule et dont le dénominateur est celui choisi à l'étape 1.||\displaystyle 0,54=\frac{54}{100}||
3. Simplifier la fraction au besoin.||\displaystyle \frac{54\color{green}{\div 2}}{100\color{green}{\div 2}}=\frac{27}{50}||
Ainsi, |\displaystyle 0,54=\frac{27}{50}|.
Exprime |0,333| en fraction irréductible.
1. Observer le nombre de chiffres après la virgule du nombre décimal pour déterminer le dénominateur à utiliser.
On remarque qu'il y a trois chiffres après la virgule dans |0,333|. On utilisera le nombre |\small 1000| comme dénominateur.
2. Écrire une fraction dont le numérateur est le nombre décimal sans la virgule et dont le dénominateur est celui choisi à l'étape 1.||\displaystyle 0,333=\frac{333}{1000}||
3. Simplifier la fraction au besoin.
La fraction ne peut pas être plus simplifiée ici.
On a donc |\displaystyle 0,333=\frac{333}{1000}|.