Here is some basic information about the step function.
For additional information, consult the following concept sheets.
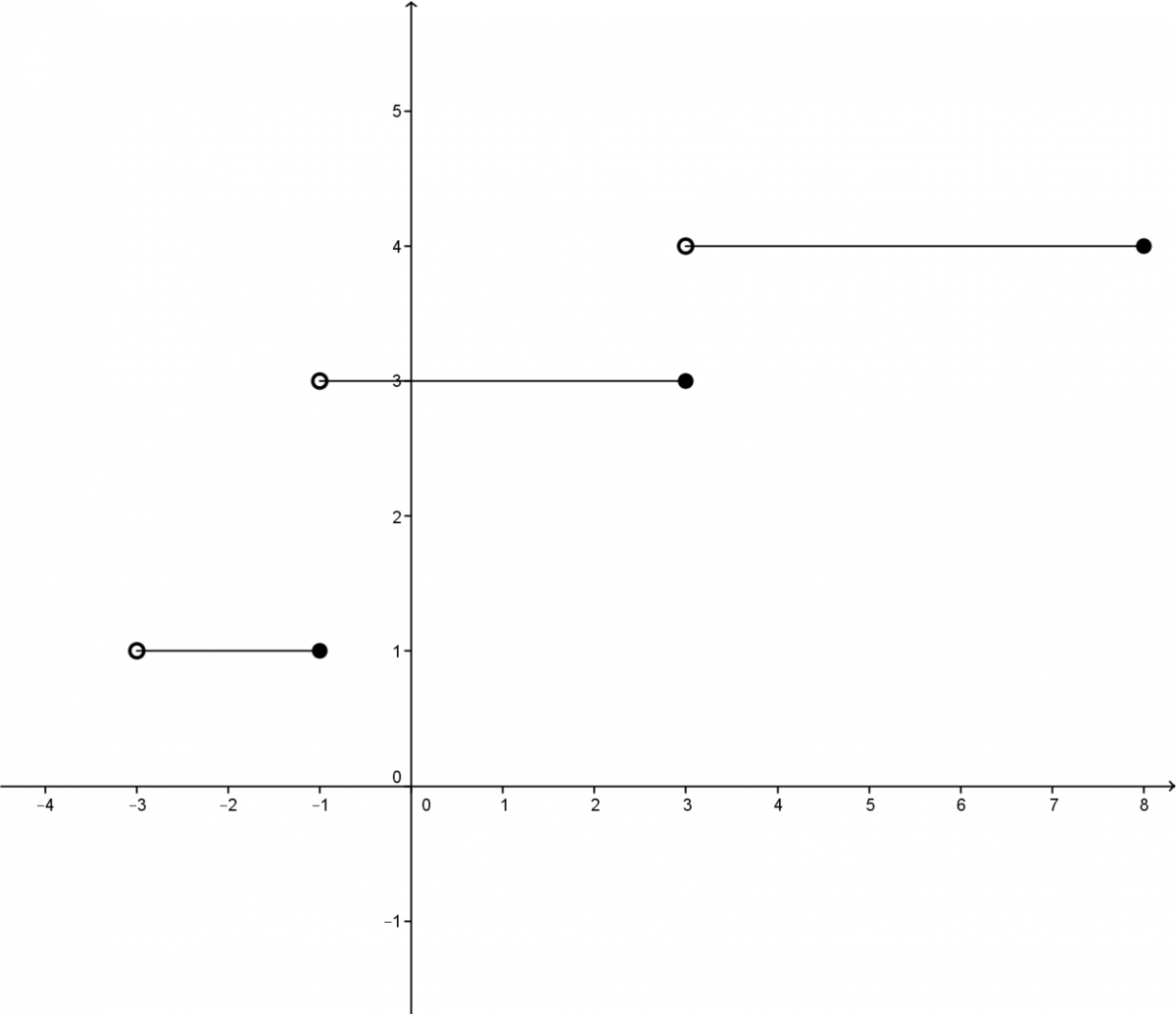
A function that is constant over intervals is called a step function. It is formed by platforms which are called steps. The vertical distance between the steps is informally called the step height.
A step function does not always have steps of the same length. The same is true for the step heights.
Here is an example graph of a step function.
Pour valider ta compréhension à propos de la résolution graphique de fonctions en escalier, périodiques et définies par parties de façon interactive, consulte la MiniRécup suivante.

It is useful here to define the integer component of a number.
The integer part of a number, denoted |[x],| is the unique integer such that |[x] \leq x < [x] +1.| This quantity is also called the greatest integer less than or equal to |x.| The two names are synonymous.
Note: If |[x]=a|, where |a| is an integer, then |a \leq x < a+1.| Therefore, |x| belongs to the interval |[a,a+1[.|
|[2.3]=2,| we look for the largest integer less than or equal to |2.3.| Note that |2 \leq 2.3 < 3.|
|[-2.3]=-3,| we look for the largest integer less than or equal to |-2.3.| Note that |-3 \leq -2.3 < -2.|
|[45]=45,| we look for the largest integer less than or equal to |45.| Note that |45 \leq 45 < 46.|
The greatest integer function is a particular kind of step function.
A step function is a function |f|, such that for any real number |x|, |f(x)| is less than or equal to |x|.
The step function in its basic form has the following equation.
||f(x)=[x]||
In this function, the steps all have the same length and the step heights all have the same length as well |(1)|.
From now on, the term step function will refer to the greatest integer function specifically.
Here is the graph of the basic step function along with its table of values.
| |x| | |y| |
|---|---|
| |[-5,-4[| | |-5| |
| |[-4,-3[| | |-4| |
| |[-3,-2[| | |-3| |
| |[-2,-1[| | |-2| |
| |[-1,0[| | |-1| |
| |[0,1[| | |0| |
| |[1,2[| | |1| |
| |[2,3[| | |2| |
| |[3,4[| | |3| |
| |[4,5[| | |4| |
| |[5,6[| | |5| |
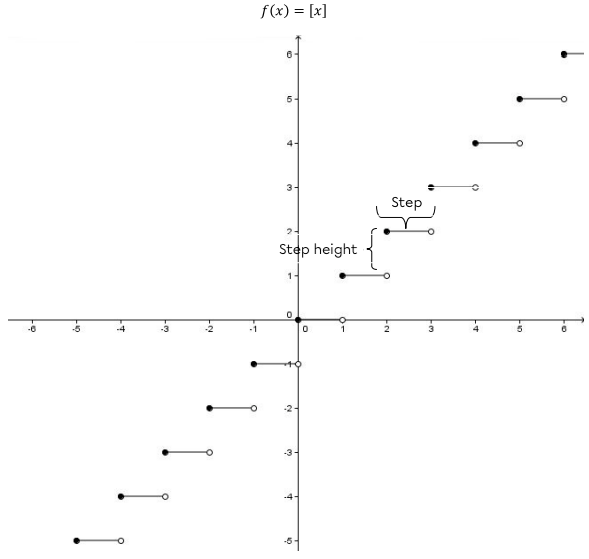
Open, or undefined, points are not part of the function. For instance, |[-1] \neq -2,| rather |[-1]=-1.| So it is normal that the point |(-1,-2)| is open and the point |(-1,-1)| is closed.
It is important to understand that, for a certain value of |f(x)|, the values of |x| correspond to an interval which has a closed end (defined point) and an open end (empty point). Each |x| in this interval maps to the same |f(x)|. This results in a platform, thus, the term step.