There are several situations to consider when finding the rule of an exponential function.
When finding the rule of an exponential function from a graph or a table of values, avoid the form |y=a_1(c_1)^{b(x-h)}| since it is equivalent to |y=a_2(c_2)^x|.
However, the role of the parameter |b| of the form |y=a(c)^{bx}| is useful when representing an actual situation, since it corresponds to how the percent change is calculated.
Here is an algebraic proof demonstrating the equations |y=a_1(c_1)^{b(x-h)}| and |y=a_2(c_2)^x| are perfectly equivalent. ||\begin{align}
y &= a_1(c_1)^{b(x-h)}\\
&= a_1\left(\color{blue}{(c_1)^{b}}\right)^{x-h} &&\text{since } a^{mn} = (a^m)^{^{\Large n}}\\
&= a_1\, \large{(\color{blue}{c_2})}\normalsize^{x-h} &&\text{substituting }\color{blue}{(c_1)^{b}} \ \text{with a new variable : }\large\color{blue}{c_2}\\
&= a_1 \dfrac{(c_2)^{x}}{(c_2)^h} &&\text{since } a^{m-n}=\dfrac{a^m}{a^n}\\
&= \color{red}{\dfrac{a_1}{(c_2)^h}}(c_2)^{x} &&\text{by the associative property: }a\times \frac{b}{c}=\dfrac{a}{c} \times b\\
&= \ \ \large \color{red}{a_2}(c_2)^x &&\text{substituting }\color{red}{\dfrac{a_1}{(c_2)^h}} \ \text{with a new variable: }\large\color{red}{a_2}
\end{align}||
For example, the functions |y=24(2)^{3(x-1)}| and |y=3(8)^x| are perfectly equivalent. Here is the proof. ||\begin{align}
y &= 24(2)^{3(x-1)}\\
&= 24\left(2^3\right)^{x-1} &&\text{since } a^{mn} = (a^m)^{^{\Large n}}\\
&= 24(8)^{x-1} &&\text{since } 2^3=8\\
&= 24\dfrac{(8)^x}{(8)^1}&&\text{since } a^{m-n}=\dfrac{a^m}{a^n}\\
&= \dfrac{24}{8}(8)^x &&\text{since }8^1=8\\
&= 3(8)^x &&\text{since } \dfrac{24}{8}=3
\end{align}||
In conclusion, if the graph of the function exists, it is much easier to find the equation |y=3(8)^x| than the other equation. There are only |2| parameters to determine |(a=3| and |c=8)| instead of |4|, which is half the work!
It is possible to find the rule by using two methods. These methods are not equivalent, but complementary, since they must be used in very specific situations.
As soon as the coordinates of the |y|-intercept are known, this method can be applied.
-
Find the value of parameter |a| by substituting the coordinates of the |y|-intercept into the basic equation |y=a(c)^x|.
-
Find the value of the base |c| using the coordinates of the other point.
What is the rule of the curve shown below?
-
Find the parameter value |a| by substituting the coordinates of the |y|-intercept into the basic equation |y=a(c)^x|
According to the law of exponents, the result is: ||\begin{align} y &= a(c)^x \\ -5 &= a(c)^{0} \\ -5 &= a (1) \\ -5 &= a \end{align}|| -
Find the value of the base |c| using the coordinates of the other point
From the information found in step |1|, use the coordinates of the other point. ||\begin{align} y &= -5(c)^x \\ \frac{-5}{3} &= -5 (c)^{-1}\\ \frac{-5}{-15} &= (c)^{-1}\\ \frac{1}{3} &= (c)^{-1}\\ \frac{1}{3} &= \frac{1}{c}\\ c &= 3 \end{align}||
Note: The negative exponent is one of the laws of exponents which is essential to solve the problem.
Answer: The rule of the function is |y=-5(3)^{x}.|
For this type of situation in particular, using the comparison method is unavoidable.
-
Substitute each point into the equation to create a system of equations.
-
Determine the value of the base |c| by the comparison method.
-
Use one of the two points provided to find the value of the parameter |a.|
Determine the rule of the curve passing through the points |\left(2,\dfrac{-9}{2}\right)| and |\left(-2,\dfrac{-8}{9}\right).|
-
Substitute each of the points into the equation to create a system of equations
1st coordinates
2nd coordinates
||\begin{align} y &= a(c)^x \\\\ \frac{-9}{2} &= a(c)^2 \\\\ \frac{-9}{2(c)^2} &= a \end{align}||
||\begin{align} y &= a(c)^x \\\\ \frac{-8}{9} &= a(c)^{-2} \\\\ \frac{-8}{9(c)^{-2}} &= a \end{align}||
-
Find the value of the base |c| using the comparison method ||\begin{align} a &= a \\\\ \frac{-9}{2(c)^2} &= \frac{-8}{9(c)^{-2}} \\\\ -9 (9)(c)^{-2} &= -8 (2)(c)^2 \\\\ -81 &= \frac{-16(c)^2}{(c)^{-2}} \\\\ -81 &= -16(c)^{2 -^-2} &\text{(law of exponents)} \\\\ \sqrt[4]{\frac{-81}{-16}} &= \sqrt[4]{(c)^4} \\\\ 1.5 &= c \end{align}||
-
Use one of the two points provided to find the value of the parameter |a| ||\begin{align} y &= a (1{.}5)^x \\\\ \frac{-9}{2} &= a (1.5)^2 \\\\ \frac{-9}{2} \color{red}{\div 2.25} &= a (2.25) \color{red}{\div 2.25}\\\\ -2 &= a \end{align}||
Answer: The rule of the exponential function is |y=-2(1.5)^x.|
It is more convenient to use the simplified form |(y=a(c)^x+k)| than using the standard form |(y=a(c)^{b(x-h)}+k).| This form is obtained using laws of exponents.
Note: However, the value of parameter |a| in the simplified form is not the same as in the standard form. The same goes for the value of the base |c|.
For this type of situation, using the comparison method is necessary.
-
Replace |k| with the value of the asymptote.
-
Substitute in each of the points to create a system of equations.
-
Determine the value of the base |c| using the comparison method.
-
Use one of the two points provided to find the value of the parameter |a.|
Find the rule of the function represented in the Cartesian plane below.
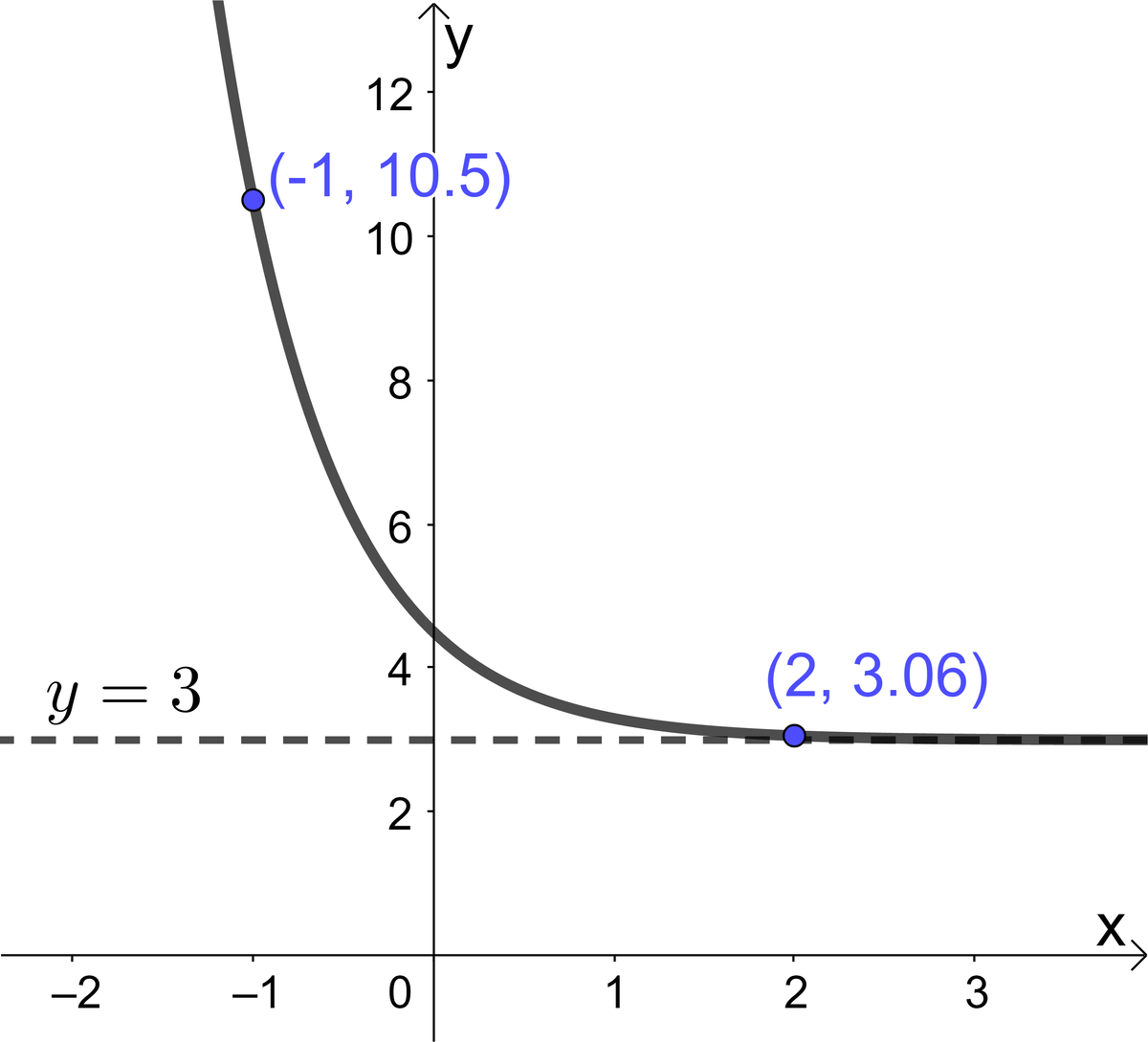
-
Replace |k| by the value of the asymptote ||\begin{align} y& = a(c)^x + \color{blue}{k} \\ y&=a(c)^x+\color{blue}{3} \end{align}||
-
Substitute in each of the points to create a system of equations
1st coordinates
2nd coordinates
||\begin{align} y &= a(c)^x+3 \\ 10.5 &= a(c)^{-1}+3 \\ 7.5 &= a(c)^{-1} \\ \dfrac{7.5}{(c)^{-1}} &= a \end{align}||
||\begin{align} y &= a(c)^x+3 \\ 3.06 &= a(c)^{2}+3 \\ 0.06 &= a(c)^{2} \\ \dfrac{0.06}{(c)^{2}} &= a \end{align}||
-
Determine the value of the base |c| using the comparison method ||\begin{align} a & = a \\\\ \frac{7.5}{(c)^{-1}} & = \frac{0.06}{(c)^{2}} \\\\ \frac{(c)^2}{(c)^{-1}} & = \frac{0.06}{7.5} \\\\ (c)^{2-(\text{-}1)} & = 0.008 && (\text{law of exponents}) \\\\ \sqrt[3]{(c)^3} & = \sqrt[3]{0.008} \\\\ c & = 0.2\end{align}||
-
Use one of the two points provided to find the value of the parameter |a| ||\begin{align} y &= a (0.2)^x+3\\\\ 3.06 &= a (0.2)^2+3 \\\\ 0.06 \color{red}{\div 0.04} &= a (0{}04) \color{red}{\div 0.04} \\\\ 1.5 &= a \end{align}||
Answer: The rule of the exponential function is |y=1.5(0.2)^x+3.|
In the last example, it is possible to apply another technique for solving a system of equations other than the comparison method. This is an elimination method using division. Look at the following example.
After obtaining the 2 equations |7.5=a(c)^{-1}| and |0.06=a(c)^2,| divide them like so: ||\begin{align} \frac{7.5}{0.06} &= \frac{a(c)^{-1}}{a(c)^2} \\ 125 &= a^{1-1}(c)^{-1-2}\end{align}|| Since |a^{1-1}=a^0=1,| |a| disappears. ||\begin{align}125 &=\frac{1}{(c)^3}\\ (c)^3 &= \frac{1}{125}\\ \sqrt[3]{(c)^3} &= \sqrt[3]{\frac{1}{125}} \\ c &= \frac{\sqrt[3]{1}}{\sqrt[3]{125}} = \frac{1}{5} = 0.2 \end{align}|| Obviously, we get the same result with this strategy.
With the exponential function, there is a multiplying factor between the changes in the dependent variable every time the independent variable increases by |1|. The multiplying factor corresponds to the base of the function.
The following is the table of values of the function |y=2(3)^x-1|.
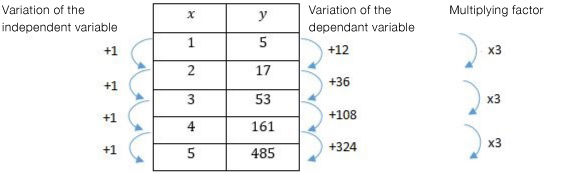
Note the multiplying factor is |3| and that it corresponds to the base |c| of the exponential function.
-
Find the variations of the dependent variable (the changes in the independent variable must be |1|) to determine the multiplying factor |(c).|
-
Substitute two |(x,y)| coordinate pairs into the equation |y=a(c)^x+k.|
-
Isolate |k| in both equations.
-
Solve the system of equations algebraically to find the value of the parameter |a.|
-
Replace |a| in either of the two equations to find the value of the parameter |k.|
-
Write the rule of the exponential function.
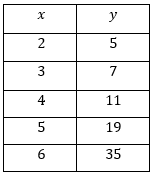
The rule of the exponential function of the form |y=a(c)^x+k| is shown in the following table of values.
-
Determine the variations of the dependent variable (changes in the independent variable must be |1|) to find the multiplying factor |(c)|

Therefore, the base |(c)| is 2.
-
Substitute two |(x,y)| coordinate pairs into the equation |y=a(c)^x+k|
Using |(2,5)| and |(5,19),| the result is: ||\begin{align}
&5=a(2)^2+k && \text{and} && 19=a(2)^5+k\\ & 5 = 4a + k && \text{and} && 19 = 32a + k \end{align}|| -
Isolate |k| in both equations ||\begin{align} &5=a(2)^2+k && \text{and} && 19=a(2)^5+k\\ & 5=4a+k && \text{and} && 19=32a+k\\ & 5 - 4a = k && \text{and} && 19 - 32a=k \end{align}||
-
Solve the system of equations algebraically to find the value of the parameter |a|
Using the comparison method, the result is: ||\begin{align} 5-4a&= 19-32a\\ 5&= 19-28a\\ -14&= -28a\\ 0.5&=a\end{align}|| -
Replace |a| in either of the two equations to find the value of the parameter |k| ||\begin{align}
5 & = 4a + k \\
5 & =4 (0.5) + k \\
5 & = 2 + k \\
3 &= k \end{align}|| -
Write the rule of the exponential function. ||y=0.5(2)^x+3||
Why does the method presented in the finding the equation of an exponential function of the form |y=a(c)^x+k| work?
The following is the proof.
Without loss of generality, take three consecutive coordinate pairs whose |x|-coordinates increase by |1|, such as |(x_1,y_1),(x_2,y_2),(x_3,y_3)|.
Thus: ||\begin{align} y_1 &= a(c)^{x_1}+k \\ y_2 &= a(c)^{x_2}+k \\ y_3 &= a(c)^{x_3}+k \end{align}||
Calculate the changes in the independent variable. ||\begin{align} y_2-y_1 &= \big(a(c)^{x_2}+k\big)-\big(a(c)^{x_1}+k\big) \\ \Rightarrow\ y_2-y_1 &=a(c)^{x_2}-a(c)^{x_1} \\\\ y_3-y_2 &= \big(a(c)^{x_3}+k\big) - \big(a(c)^{x_2}+k\big) \\ \Rightarrow\ y_3-y_2 &= a(c)^{x_3}-a(c)^{x_2} \end{align}||
At this stage, factor out a common factor from each equation. ||\begin{align} y_2-y_1 &= a\big((c)^{x_2}-(c)^{x_1}\big) \\ y_3-y_2 &= a\big((c)^{x_3}-(c)^{x_2}\big) \end{align}||
Note that |x_2=x_1+1| and |x_3=x_2+1|.
Make substitutions in the two calculated equations. ||\begin{align} y_2-y_1 &= a\big((c)^{x_1+1}-(c)^{x_1}\big) \\ y_3-y_2 &= a\big((c)^{x_2+1}-(c)^{x_2}\big) \end{align}||
Again, factor out a common factor from each equation. ||\begin{align} y_2-y_1 &= a(c)^{x_1}\big(c-1\big) \\ y_3-y_2 &= a(c)^{x_2}\big(c-1\big) \end{align}||
The only thing remaining is to divide the two equations. ||\dfrac{y_3-y_2}{y_2-y_1} = \dfrac{a(c)^{x_2}(c-1)}{a(c)^{x_1}(c-1)}||
||\dfrac{y_3-y_2}{y_2-y_1} = \frac{(c)^{x_2}}{(c)^{x_1}} = \frac{(c)^{x_1+1}}{(c)^{x_1}}||
Note, |\dfrac{(c)^{x_1+1}}{(c)^{x_1}} = \dfrac{c}{1}.|
Therefore: ||\dfrac{y_3-y_2}{y_2-y_1} = c||
This explains the variation in the values in the dependant variable; when the |x|-values are consecutive and differ by |1|, it is possible to find the base |c| of the exponential function in the form |y=a(c)^x+k|.