Graphing a Quadratic Function

To sketch the graph of a quadratic (or second-degree polynomial) function, plot a minimum of three points on a Cartesian plane.

The following points are generally sought:

1. The coordinates of the vertex.

2. The coordinates of the zeroes, if they exist.

The |y|-intercept can also be placed along with its symmetrical point (the point on the other branch at the same height).

The points that are found will give a general picture of the parabola. If more precision is required, other points of the function must be found.

Whether in the form |y=ax^2| or |y=a(bx)^2,| the vertex of this function is always located at |(0,0).|

1. Position the function’s vertex at |(0,0).|

2. Build a table of values where the same numbers (in |x|) are used: taking both the number’s positive and negative values. For example, 2 and -2, 3 and -3, etc.

3. Plot the points on a Cartesian plane and sketch the curve of the function.

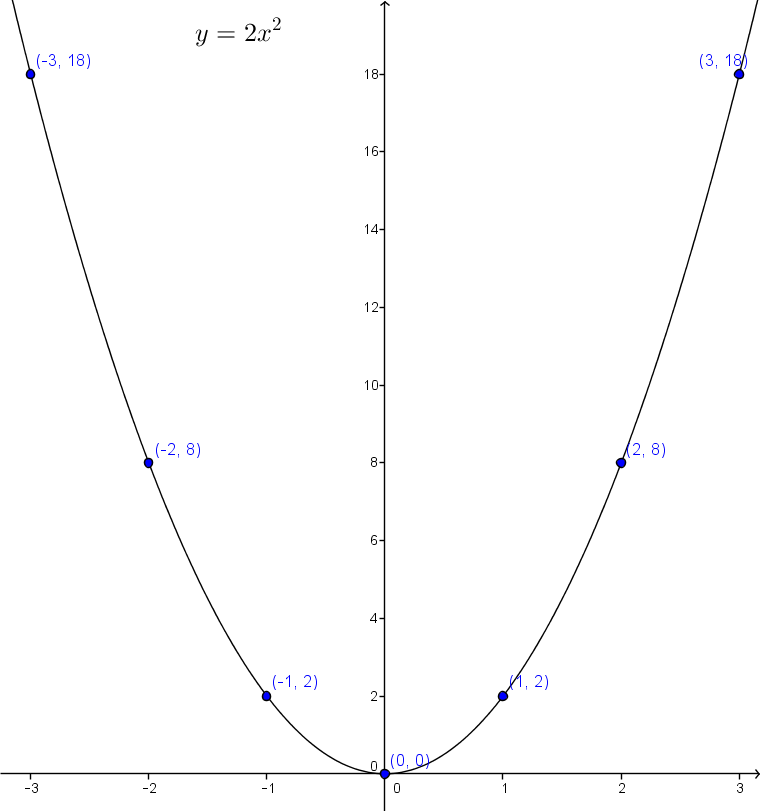
Graph the quadratic function |y=2x^2.|

1. Plot the vertex at |(0,0).|

2. Build a table of values.

   |x|	|y|
   |-3|	|18|
   |-2|	|8|
   |-1|	|2|
   |1|	|2|
   |2|	|8|
   |3|	|18|

3. Plot the points on a Cartesian plane and sketch the curve of the function.

The procedure is the same whether the function is written in the form |y=ax^2| or |y=a(bx)^2.|

1. Find the vertex’s coordinates |(h,k)| of the function by using the formula |\displaystyle (h,k) = \left(- \frac{b}{2a}, \frac{4ac-b^2}{4a} \right).|

2. Find the values of the function’s zeroes by using the quadratic formula. ||\displaystyle x_{1,2}= \frac{-b \pm \sqrt{b^2-4ac}}{2a}||

3. Position the |y|-intercept using the value of |c.| In fact, the coordinates of the intercept are |(0,c).|

4. Find the point on the other branch that is at the same height as the |y|-intercept.

Sketch the graph of the uadratic function |y=-2x^2+4x+8.|

In the function, |a=-2,| |b=4| and |c=8.|

1. The vertex’s coordinates |(h,k)| are calculated as follows.||\begin{align}(h,k) &= \left( - \dfrac{b}{2a}, \dfrac{4ac-b^2}{4a}\right) \\ &= \left(- \dfrac{4}{2 (-2)}, \dfrac{4(-2)(8) - 4^2}{4(-2)} \right) \\ &= (1,10) \end{align}||

2. The zeroes are calculated as follows.||\begin{align} x_{1,2} &=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a} \\ &= \dfrac{-4 \pm \sqrt{4^2 - 4(-2)(8)}}{2(-2)} \\ &= \dfrac{-4 \pm \sqrt{80}}{-2} \end{align}||Next, separate the formula into two parts: one using the + and the other using the -. |x_1| will be a zero and |x_2| will be the other zero.||\begin{align} x_1 &= \dfrac{-4 + \sqrt{80}}{-4} \approx -1{,}24 \\ x_2 &= \frac{-4 - \sqrt{80}}{-4} \approx 3{,}24 \end{align}||Therefore, we have the two points |(-1.24;0)| and |(3.24;0).|

3. Since |c=8,| the point |(0,8)| is obtained.

4. To find the point on the other branch that is at the same height as the |y|-intercept, use the axis of symmetry. The equation is |x=h,| so |x=1.| Therefore, the other point will have the coordinates |(2,8).|

We can now plot the points on a Cartesian plane and graph the function.

1. From the equation of the function, determine the coordinates of the vertex |(h,k).|

2. Find the values of the zeroes of the function by replacing |y| with |0| and isolating |x,| or by using the following formula. ||\displaystyle x_{1,2}= h \pm \sqrt{-\frac{k}{a}}||

3. Calculate the |y|-intercept.

4. Find the point on the other branch that is at the same height as the |y|-intercept.

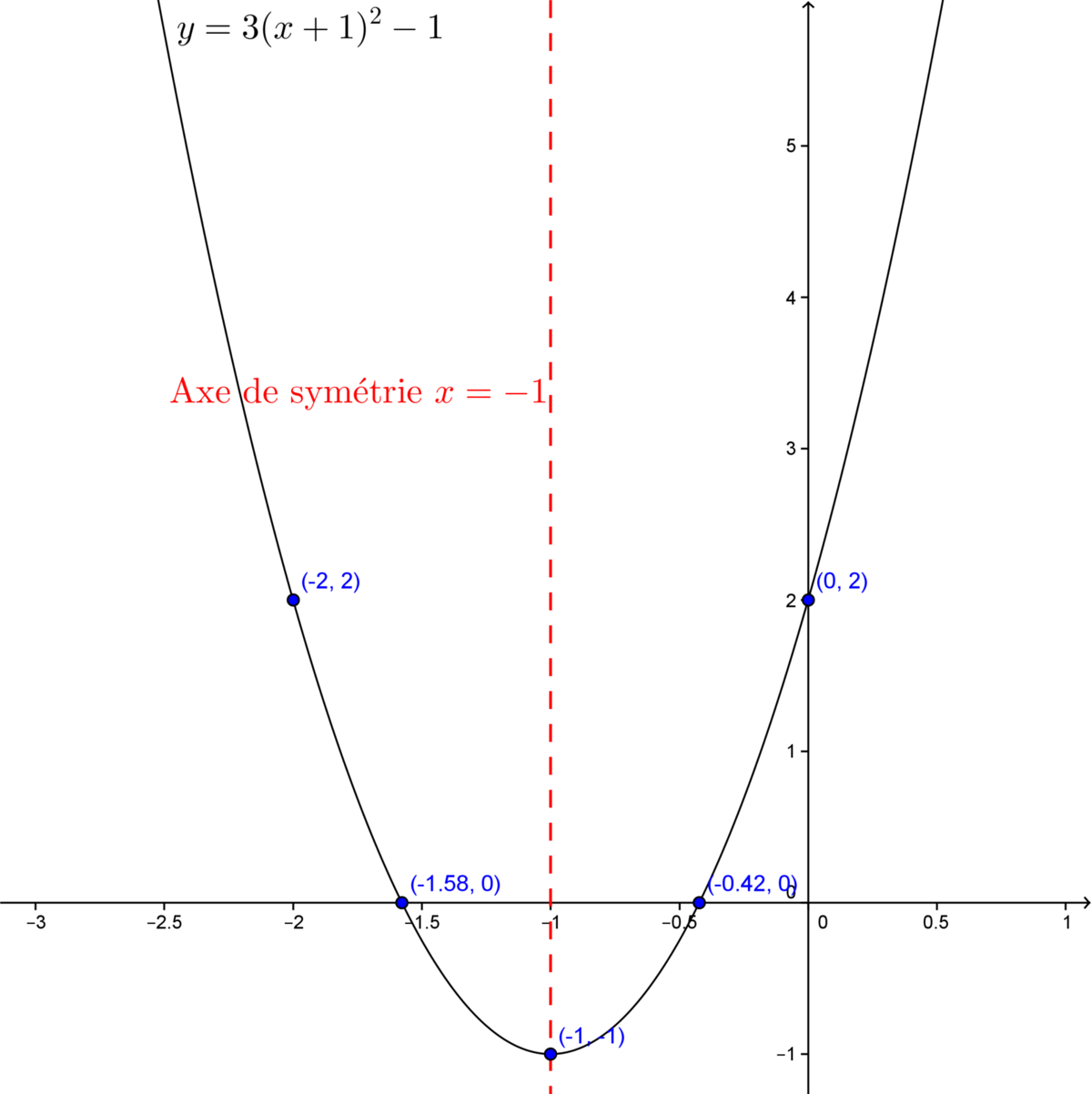
Graph the following quadratic function |y=3(x+1)^2-1.|

1. The vertex’s coordinates of the function are |(-1,-1).| In this case, |a(x-h)^2+k=3(x-(-1))^2-1.|

2. Calculate the zeroes by replacing |y| with |0| and isolating |x|, or by using the formula.||\begin{align} 0 &= 3(x+1)^2 -1 \\ 1 &= 3(x+1)^2 \\ \dfrac{1}{3} &= (x+1)^2 \\ \pm \dfrac{1}{3} &= x+1\quad (\text{ne pas oublier le } \pm) \\ -1 \pm \dfrac{1}{3} &= x \end{align}||Next, separate the formula into two parts: one using the + and the other using the -. |x_1| will be a zero and |x_2| is the other zero.||\begin{align} x_1 &= -1 + \sqrt \frac{1}{3} \approx -0{,}42 \\ x_2 &= -1 - \sqrt \frac{1}{3} \approx -1{,}58 \end{align}||Therefore, the following two points are obtained: |(-0.42,0)| and |(-1.58,0).|

3. The |y|-intercept is calculated by replacing |x| by |0.|||y=3(0+1)^2 - 1 = 2||So, we have the point |(0,2).|

4. The axis of symmetry is |x=h,| in this case |x=-1.| The other point is located at the same height as the |y|-intercept and will have the coordinates |(-2,2).|

Plot the points on a Cartesian plane and graph the parabola.

1. Determine the values of the function’s two zeroes. In the factored form, |y=a(x-x_1)(x-x_2),| where |x_1| and |x_2| are the values of the zeroes.

2. Find the coordinates of the function’s vertex. The vertex’s |x|-value is given by the midpoint formula |\displaystyle h = \frac{x_1 + x_2}{2}|.
   To find the |y|-value of the vertex (|k|), replace |x| with the value of |h| in the equation of the function.

3. Calculate the |y|-intercept.

4. Find the point on the other branch that is at the same height as the |y|-intercept.

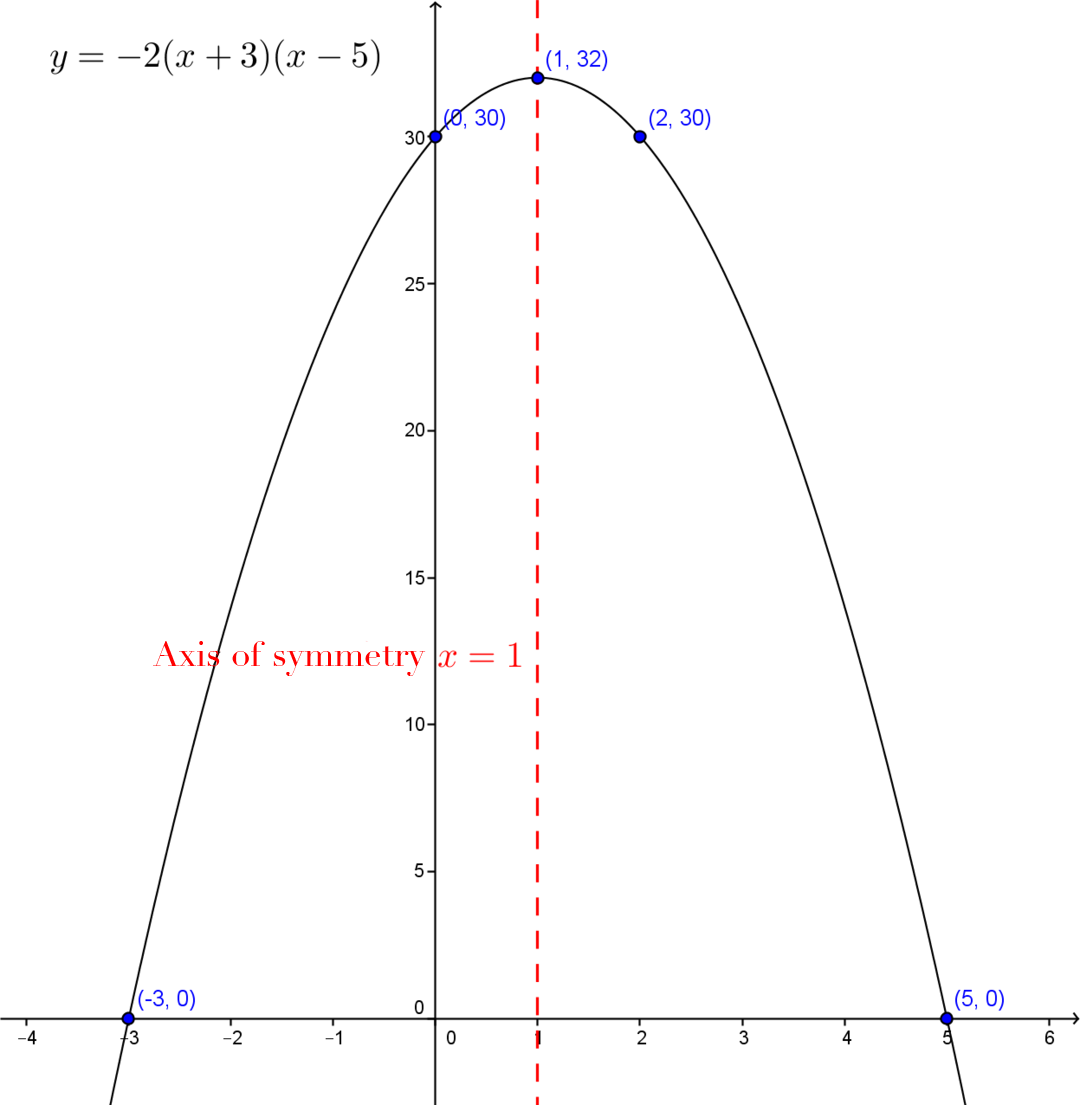
Graph the following quadratic function: |y=-2(x+3)(x-5).|

1. The values of the zeroes are |x_1=-3| and |x_2=5.| In this case, |a(x-x_1)(x-x_2)=a(x-(-3))(x-5).| The points |(-3,0)| and |(5,0)| are obtained.

2. The vertex’s |x|-value t is calculated as follows.||\begin{align} h &= \dfrac{x_1+x_2}{2} \\ &= \dfrac{-3 + 5}{2} \\ &= 1 \end{align}||By replacing |x| with |1| in the equation, the |y|-value of the vertex is obtained, i.e., the value of |k.|||\begin{align} k &= f(h) =f(1)\\ &=-2(1+3)(1-5) \\ &= 32 \end{align}||Therefore, the vertex of the function is at the point |(1,32).|

3. The |y|-intercept is calculated by replacing |x| with |0.|||f(0)=-2(0+3)(0-5) = 30||So, the point |(0,30)| is obtained.

4. The axis of symmetry equation is |x=h|, in this case |x=1.| The other point is located at the same height as the |y|-intercept and has coordinates |(2,30).|

Plot the points on a Cartesian plane and graph the parabola.