Tracer une fonction polynomiale de degré 2

De façon générale, pour tracer une fonction polynomiale de degré 2, il est préférable de placer un minimum de 3 points dans un plan cartésien.

On recherche généralement les points suivants :

1. Les coordonnées du sommet.

2. Les coordonnées des zéros, s'il y en a.

On peut aussi positionner l'ordonnée à l'origine et son point symétrique (celui à la même hauteur).

Les points trouvés vont donner une vue générale de la parabole. S'il faut plus de précision, on doit rechercher d'autres points de la fonction.

Que ce soit dans la forme |y=ax^2| ou dans la forme |y=a(bx)^2|, le sommet de la fonction est toujours situé à |(0,0)|.

1. Positionner le sommet de la fonction à |(0,0).|

2. Bâtir une table de valeurs dans laquelle on utilise les mêmes nombres (en |x|) en prenant le positif et le négatif. Par exemple, 2 et -2, 3  et -3, etc.

3. Placer les points dans le plan cartésien et tracer la fonction.

Trace la fonction polynomiale de degré 2 suivante : |y=2x^2|

1. On positionne le sommet à |(0,0).|

2. On bâtit une table de valeurs.

   |x|	|y|
   |-3|	|18|
   |-2|	|8|
   |-1|	|2|
   |1|	|2|
   |2|	|8|
   |3|	|18|

3. On positionne les points dans un plan cartésien et on trace la fonction.

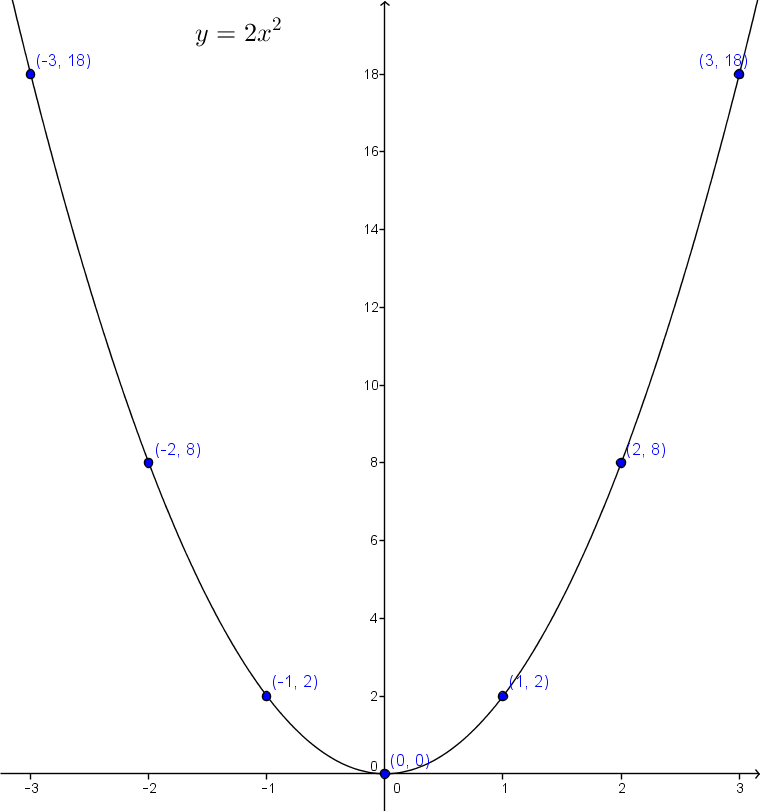
La démarche est la même que la fonction soit écrite sous la forme |y=ax^2| ou sous la forme |y=a(bx)^2|.

1. Retrouver les coordonnées du sommet |(h,k)| de la fonction en utilisant les formules |(h,k) = \left(- \dfrac{b}{2a}, \dfrac{4ac-b^2}{4a} \right).|

2. Trouver les valeurs des zéros de la fonction avec la formule quadratique. ||x_{1,2}= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}||

3. Positionner l'ordonnée à l'origine en utilisant la valeur de |c.| En fait, les coordonnées de l'ordonnée à l'origine sont |(0,c).|

4. Trouver le point situé à la même hauteur que l'ordonnée à l'origine.

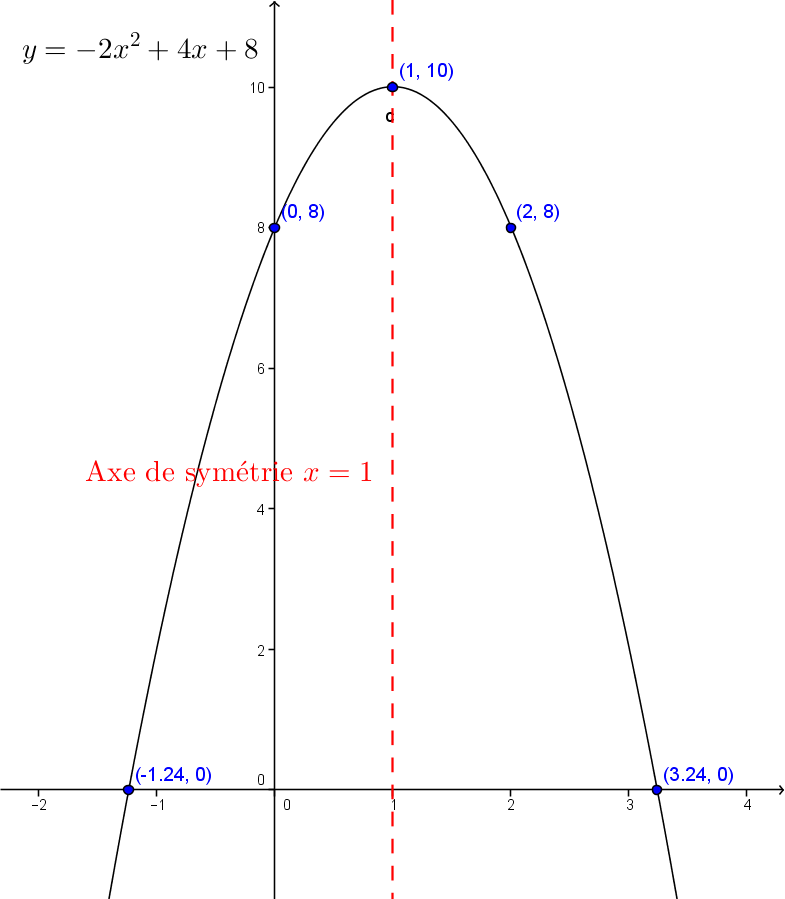
Trace le graphique de la fonction |y=-2x^2+4x+8.|

Dans cette fonction, |a=-2,| |b=4| et |c=8.|

1. On calcule les coordonnées du sommet |(h,k).| ||\begin{align}(h,k) &= \left( - \dfrac{b}{2a}, \dfrac{4ac-b^2}{4a}\right) \\ &= \left(- \dfrac{4}{2 (-2)}, \dfrac{4(-2)(8) - 4^2}{4(-2)} \right) \\ &= (1,10) \end{align}||

2. On calcule les zéros. ||\begin{align} x_{1,2} &=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a} \\ &= \dfrac{-4 \pm \sqrt{4^2 - 4(-2)(8)}}{2(-2)} \\ &= \dfrac{-4 \pm \sqrt{80}}{-2} \end{align}||Rendu ici, il faut séparer la formule en deux parties : l'une utilisant le |+| et l'autre utilisant le moins. |x_1| sera un zéro et |x_2| sera l'autre zéro. ||\begin{align} x_1 &= \dfrac{-4 + \sqrt{80}}{-4} \approx -1{,}24 \\ x_2 &= \frac{-4 - \sqrt{80}}{-4} \approx 3{,}24 \end{align}||Ainsi, on a les deux points |(-1{,}24;0)| et |(3{,}24;0).|

3. Comme |c=8,| on a le point |(0,8).|

4. Pour trouver le point situé à la même hauteur que l'ordonnée à l'origine, il faut utiliser l'axe de symétrie dont l'équation est |x=h| donc |x=1.| Ainsi, l'autre point aura comme coordonnées |(2,8).|

On peut maintenant mettre les points dans un plan cartésien et tracer la fonction.
 

1. À partir de l'équation de la fonction, déterminer les coordonnées du sommet |(h,k).|

2. Trouver les valeurs des zéros de la fonction en remplaçant |y| par |0| puis en isolant |x| ou en utilisant directement la formule |x_{1,2}= h \pm \sqrt{-\dfrac{k}{a}}.|

3. Calculer l'ordonnée à l'origine.

4. Trouver le point situé à la même hauteur que l'ordonnée à l'origine.

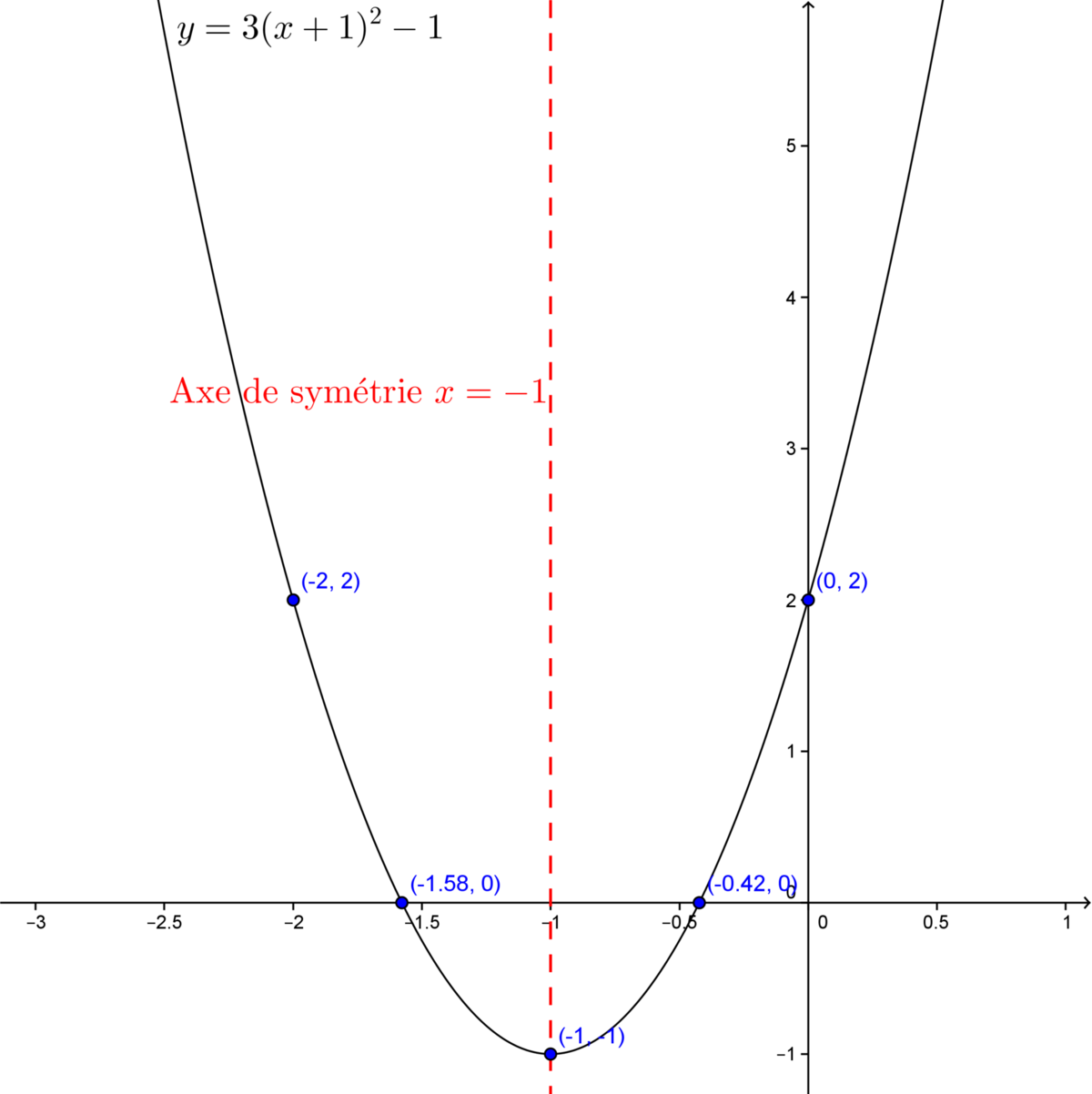
Trace le graphique la fonction polynomiale de degré 2 suivante : |y=3(x+1)^2-1.|

1. Les coordonnées du sommet de la fonction sont |(-1,-1).| En effet, ici |a(x-h)^2+k=3\big(x-(-1)\big)^2-1.|

2. On calcule les zéros en remplaçant |y| par |0| puis en isolant |x| (ou en utilisant la formule). ||\begin{align} 0 &= 3(x+1)^2 -1 \\ 1 &= 3(x+1)^2 \\ \dfrac{1}{3} &= (x+1)^2 \\ \pm\sqrt{\dfrac{1}{3}} &= x+1\quad (\text{ne pas oublier le } \pm) \\ -1 \pm \sqrt{\dfrac{1}{3}} &= x \end{align}||Rendu ici, il faut séparer la formule en deux parties : l'une utilisant le |+| et l'autre utilisant le |-.| |x_1| sera un zéro et |x_2| sera l'autre zéro. ||\begin{align} x_1 &= -1 + \sqrt \frac{1}{3} \approx -0{,}42 \\ x_2 &= -1 - \sqrt \frac{1}{3} \approx -1{,}58 \end{align}||Ainsi, on a les deux points |(-0{,}42;0)| et |(-1{,}58;0).|

3. L'ordonnée à l'origine se calcule en remplaçant |x| par |0.| ||y=3(0+1)^2 - 1 = 2||On a donc le point |(0,2).|

4. L'axe de symétrie étant |x=h,| dans notre cas |x=-1.| Le point situé à la même hauteur que l'ordonnée à l'origine aura comme coordonnées |(-2,2).|

1. Déterminer les valeurs des deux zéros de la fonction. Dans la forme factorisée, |y=a(x-x_1)(x-x_2)| où |x_1| et |x_2| sont les valeurs des zéros.

2. Trouver les coordonnées du sommet de la fonction. L'abscisse du sommet est donnée par la formule du point milieu : |h = \dfrac{x_1 + x_2}{2}.|
   Pour trouver l'ordonnée du sommet |(k),| on remplace |x| par la valeur de |h| dans l'équation de la fonction.

3. Calculer l'ordonnée à l'origine.

4. Trouver le point situé à la même hauteur que l'ordonnée à l'origine.

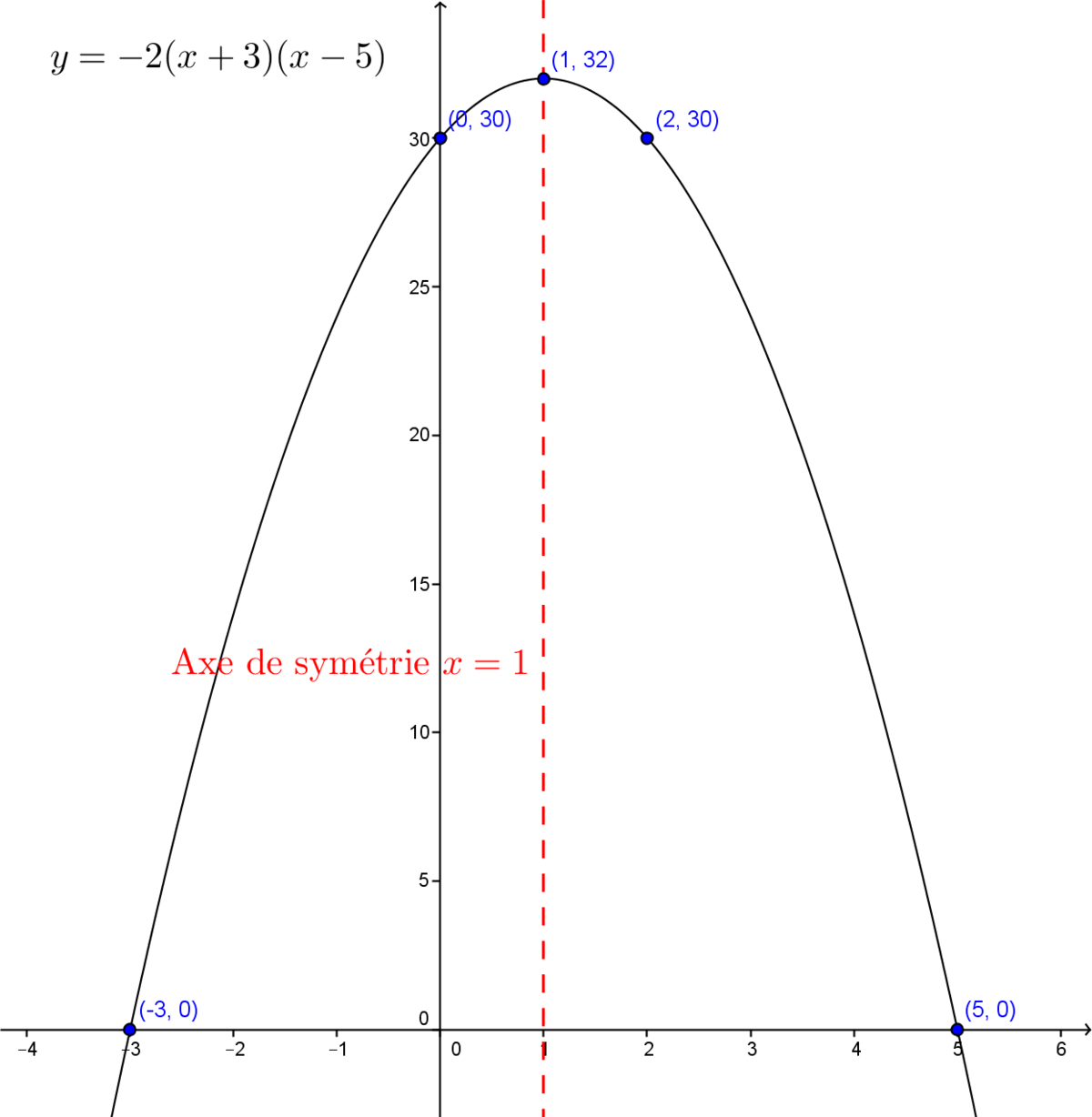
Trace le graphique de la fonction polynomiale de degré 2 suivante : |f(x)=-2(x+3)(x-5)|

1. Les valeurs des zéros sont |x_1=-3| et |x_2=5.| En effet, |a(x-x_1)(x-x_2)=a(x-(-3))(x-5).|  On a donc les points |(-3,0)| et |(5,0).|

2. On calcule l'abscisse du sommet. ||\begin{align} h &= \dfrac{x_1+x_2}{2} \\ &= \dfrac{-3 + 5}{2} \\ &= 1 \end{align}||De plus, en remplaçant |x| par |1| dans l'équation, on obtient l'ordonnée du sommet, c'est-à-dire la valeur de |k.| ||\begin{align} k &= f(h) =f(1)\\ &=-2(1+3)(1-5) \\ &= 32 \end{align}||Ainsi, le sommet de la fonction se situe au point |(1,32).|

3. L'ordonnée à l'origine se calcule en remplaçant |x| par |0.| ||f(0)=-2(0+3)(0-5) = 30||On a donc le point |(0,30).|

4. L'axe de symétrie a pour équation |x=h,| dans notre cas |x=1.| Le point situé à la même hauteur que l'ordonnée à l'origine a pour coordonnées |(2,30).|

On peut mettre les points dans un plan cartésien et tracer la fonction.