The quadratic formula is used to solve second-degree equations with the form |ax^2+bx+c=0| where |a \not= 0.|
||x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}||
-
Convert the second-degree equation to the form |ax^2+bx+c=0| to determine |a,| |b| and |c.|
-
Replace the values for |a,| |b| and |c| in the quadratic formula and calculate.
-
State the solution(s).
When solving the problem, the symbol |\pm| indicates that we must separate the formula in two: one with |+| and the other with |-.|
||\begin{align}x_1&=\dfrac{-b\color{#ec0000}+\sqrt{b^2-4ac}}{2a}\\\\x_2&=\dfrac{-b\color{#ec0000}-\sqrt{b^2-4ac}}{2a}\end{align}||
Solve the equation |-5x^2+3.5x-1=-4.|
-
Convert the second-degree equation to the form |ax^2+bx+c=0| to determine |a,| |b| and |c|
||\begin{aligned}-5x^2+3.5x-1&=-4\\\color{#ec0000}{-5}x^2+\color{#3b87cd}{3.5}x+\color{#3a9a38}3&=0\end{aligned}\\\\\begin{aligned}\\\color{#ec0000}a=\color{#ec0000}{-5}, \ \color{#3b87cd}b=\color{#3b87cd}{3.5},\ \color{#3a9a38}c=\color{#3a9a38}3\end{aligned}|| -
Replace the values for |a,| |b| and |c| in the quadratic formula and calculate
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\&=\dfrac{-\color{#3b87cd}{3.5}\pm\sqrt{\color{#3b87cd}{3.5}^2-4(\color{#ec0000}{-5})(\color{#3a9a38}3)}}{2(\color{#ec0000}{-5})}\\&=\dfrac{-3.5\pm\sqrt{12.25+60}}{-10}\\&=\dfrac{-3.5\pm\sqrt{72.25}}{-10}\\&=\dfrac{-3.5\pm8.5}{-10}\end{align}|| ||\begin{aligned}x_1&=\dfrac{-3.5+8.5}{-10} \\&=\dfrac{5}{-10}\\&=-0.5\end{aligned}\qquad\begin{aligned}x_2&=\dfrac{-3.5-8.5}{-10}\\&=\dfrac{-12}{-10}\\&=1.2\end{aligned}||
-
State the solution(s)
The solutions for the equation |-4=-5x^2+3.5x-1| are |-0.5| and |1.2.|
The graph indicates that the parabola of the equation |f(x)=-5x^2+3.5x-1| intersects the line of the equation |\color{#ff55c3}{y=-4}| at two places: at |x=-0.5| and |x=1.2.|
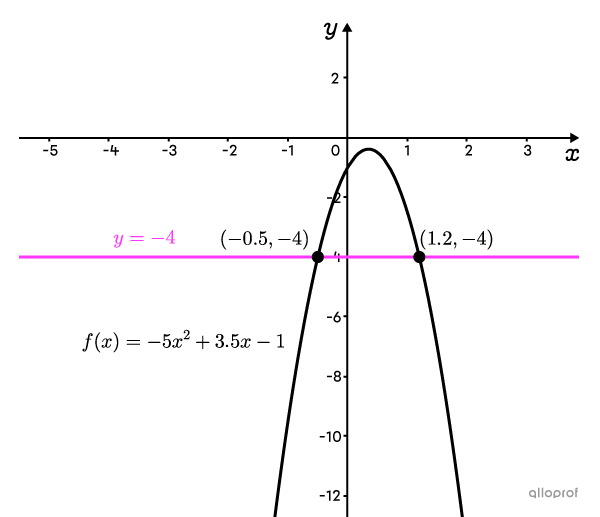
The following is an example where the quadratic formula is used to find the zeros of a second-degree polynomial function.
Find the zeros of the second-degree polynomial function with the equation |f(x)=-3x^2+8x-10.|
When looking for the zeros of a function, replace |f(x)| with |0| and isolate |x.| ||\begin{align} f(x)&=-3x^2+8x-10\\0&=-3x^2+8x-10\end{align}||
-
Convert the second-degree equation to the form |ax^2+bx+c=0| to determine |a,| |b| and |c|
The equation is already in the correct form.||\begin{align}0&=\color{#ec0000}{-3}x^2+\color{#3b87cd}8x\color{#3a9a38}{-10}\\\\ \color{#ec0000}a&=\color{#ec0000}{-3}, \ \color{#3b87cd}b=\color{#3b87cd}{8},\ \color{#3a9a38}c=\color{#3a9a38}{-10}\end{align}|| -
Replace the values for |a,| |b| and |c| in the quadratic formula and calculate
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\ &=\dfrac{-\color{#3b87cd}8\pm\sqrt{\color{#3b87cd}8^2-4(\color{#ec0000}{-3})(\color{#3a9a38}{-10})}}{2(\color{#ec0000}{-3})}\\&=\dfrac{-8\pm\sqrt{64-120}}{-6}\\&=\dfrac{-8\pm\sqrt{-56}}{-6}\end{align}|| Since it is impossible to extract the square root of a negative number, the calculation ends here and we determine the function has no zeros.
-
State the solution(s)
The function with the equation |f(x)=-3x^2+8x-10| has no zeros.
The following graph indicates that the parabola with the equation |f(x)=-3x^2+8x-10| does not intersect the |\color{#ff55c3}{x}|-axis, because it passes completely under it.

The discriminant |(\Delta)| is the expression under the root (the radicand) in the quadratic formula. ||\begin{align}x_{1,2}&=\dfrac{-b\pm\sqrt{\color{#333fb1}{\Delta}}}{2a}\\x_{1,2}&=\dfrac{-b\pm\sqrt{\color{#333fb1}{b^2-4ac}}}{2a}\end{align}||It is important to understand the relationship between the discriminant of the trinomial |ax^2+bx+c| and the number of the |ax^2+bx+c=0| equation's possible solutions.
|
|b^2-4ac>0| |
The equation has two distinct solutions. |
|
|b^2-4ac=0| |
The equation has only one solution. |
|
|b^2-4ac<0| |
The equation has no solution. |
The following is an example where the equation has only one solution.
Solve the equation |2x^2-4x+1=-1.|
-
Convert the second-degree equation to the form |ax^2+bx+c=0| to determine |a,| |b| and |c|
||\begin{aligned}2x^2-4x+1&=-1\\\color{#ec0000}2x^2\color{#3b87cd}{-4}x+\color{#3a9a38}2&=0\end{aligned}\\\\ \begin{aligned}\\\color{#ec0000}a=\color{#ec0000}{2}, \ \color{#3b87cd}b=\color{#3b87cd}{-4},\ \color{#3a9a38}c=\color{#3a9a38}2\end{aligned}|| -
Replace the values for |a,| |b| and |c| in the quadratic formula and calculate
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\ &=\dfrac{-(\color{#3b87cd}{-4})\pm\sqrt{(\color{#3b87cd}{-4})^2-4(\color{#ec0000}{2})(\color{#3a9a38}{2})}}{2(\color{#ec0000}{2})}\\ &=\dfrac{4\pm\sqrt{16-16}}{4}\\&=\dfrac{4\pm\sqrt{0}}{4}\\ &=\dfrac{4\pm 0}{4}\\ &=\dfrac{4}{4}\\&=1\end{align}|| The number under the square root is |0|, so we obtain |\pm\ 0.| Therefore, it is no longer necessary to separate the equation in two, because it has only one solution.
-
State the solution(s)
The solution of the equation |2x^2-4x+1=-1| is |x=1.|
The graph indicates that the line with the equation |\color{#ff55c3}{y=-1}| intersects the vertex of the parabola |f(x)=2x^2-4x+1.| That is why there is only one solution.

The following is the proof of the quadratic formula.
Let the equation be |ax^2+bx+c=0.| To complete the proof, we must isolate |x.| To do so, we complete the square. We start by factoring out |a.|||a\left(x^2+\dfrac{b}{a}x+\dfrac{c}{a}\right)=0||We can divide both sides of the equal sign by |a,| since |a| is not equal to |0.|||x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0||We add and subtract the term |\left(\dfrac{\frac{b}{a}}{2}\right)^2| to the left of the equation. The result is:||\begin{align}x^2+\dfrac{b}{a}x\color{#3a9a38}{+\left( \dfrac{\frac{b}{a}}{2} \right)^2}+\dfrac{c}{a}\color{#3a9a38}{- \left( \dfrac{\frac{b}{a}}{2} \right)^2}=0\\x^2+\dfrac{b}{a}x\color{#3a9a38}{+\dfrac{b^2}{4a^2}}+\dfrac{c}{a}\color{#3a9a38}{- \dfrac{b^2}{4a^2}}=0\end{align}||The first three terms on the left hand side can be factored, because they form a perfect square trinomial.||\left(x+\dfrac{b}{2a}\right)^2+\dfrac{c}{a}-\dfrac{b^2}{4a^2}=0||We put the last two terms on a common denominator.||\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a^2}=0||We subtract the fraction on each side of the equality.||\left(x+\dfrac{b}{2a}\right)^2=-\left(\dfrac{4ac-b^2}{4a^2}\right)||The |-| sign in front of the fraction is distributed to the two terms of the numerator.||\left(x+\dfrac{b}{2a}\right)^2=\dfrac{b^2-4ac}{4a^2}||We extract the square root of the two sides of the equality. Do not forget the symbol |\pm| on the right side.||\begin{align}\color{#ec0000}{\sqrt{\color{black}{\left(x+\dfrac{b}{2a}\right)^2}}} &=\color{#ec0000}{\sqrt{\color{black}{\dfrac{b^2-4ac}{4a^2}}}}\\x+\dfrac{b}{2a}&=\pm \dfrac{\sqrt{b^2-4ac}}{2a}\end{align}||The last step is to isolate |x.|||x=-\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}||The two fractions are combined.||x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}||We obtain the quadratic formula.