In probability, we sometimes have to make certain choices about a random experiment involving random quantitative variables. To do so, we can use mathematical expectation.
The mathematical expectation is the sum of a random variable's possible values multiplied by their respective probabilities.
In other words, the mathematical expectation corresponds to a weighted mean of the outcomes of a random experiment, where the weights correspond to the probability of obtaining each outcome.
Mathematical expectation is often used in the context of gambling. In this context, the mathematical expectation represents the average gain or loss that the player would have if he/she played the same game several times.
-
When the mathematical expectation is equal to 0 |(E=0),| we say that the game is fair. This means that if you play the game, on average you will not lose money, but you will not win any either. Therefore, this game is not in favour of the player or the game organizers.
-
When the mathematical expectation is negative |(E<0),| it means that, on average, the player loses money on each try. Therefore, the game is in favour of the organizers and not in favour of the player. The amount lost on each try is, on average, equal to the mathematical expectation.
-
When the mathematical expectation is positive |(E>0),| it means that, on average, the player wins money at each try. Therefore, the game is not in favour of the organizers and is in favour of the player. The amount won on each try is, on average, equal to the mathematical expectation.
In a gambling context where there is an initial bet, the mathematical expectation can be calculated in more than one way: either the initial bet is removed from each outcome, or it is removed only at the end. Both methods give exactly the same result. It is also possible that there is no initial bet.
In a mathematical expectation calculation, it is best not to reduce the fractions, since it makes adding fractions easier.
Cynthia offers the following wager to Catherine.
"Draw a random card from this |52| deck of cards. If you draw an ace, I’ll give you |\$5.| If you draw a face card, I’ll give you |\$2.| If you pick any other card, you owe me |\$1.50.|"
Should Catherine accept the wager proposed by Cynthia?
To answer this question, Catherine must calculate the mathematical expectation of the game. If she gets a negative value, she should not participate, since, on average, if she plays repeatedly, she will lose money. On the other hand, if the mathematical expectation of the game is positive, she should accept the bet, since, on average, she will win money.
The card deck contains |4| aces out of a total of |52| cards. The probability of drawing an ace is therefore |\dfrac{4}{52},| or |\dfrac{1}{13}.| This outcome is associated with a gain of |\$5.|
The card deck contains |12| face cards (|4| jacks, |4| queens and |4| kings) out of a total of |52| cards. This corresponds to a probability of |\dfrac{12}{52},| or |\dfrac{3}{13}.| This outcome is associated with a gain of |\$2.|
There are |36| other cards (cards which are not an ace, nor a king, nor a queen, nor a jack) in a deck of cards. This corresponds to a probability of |\dfrac{36}{52},| or |\dfrac{9}{13}.| This outcome is associated with a loss of |\$1.50.|
We get the following table:
|
|X| |
|\$5| |
|\$2| |
|-\ $1.50| |
|---|---|---|---|
|
|P(X)| |
|\dfrac{1}{13}| |
|\dfrac{3}{13}| |
|\dfrac{9}{13}| |
We can now calculate the mathematical expectation.
||\begin{align}E&= \dfrac{1}{13} \times 5 + \dfrac{3}{13} \times 2 + \dfrac{9}{13} \times -1.50\\&=\dfrac{5}{13}+\dfrac{6}{13}-\dfrac{13.5}{13}\\&=-\dfrac{2.5}{13}\\ &\approx -\$0.19\ \end{align}||
Answer: The mathematical expectation is negative. On average, Catherine would lose money if she accepted Cynthia's wager. Therefore, she should not accept.
Method 1: Remove the Initial Bet at the End
If we remove the bet at the end, the mathematical expectation is calculated as follows.
|ME = P(x_1)x_1 + P(x_2)x_2 + \ldots P(x_n)x_n - B|
where
|x_n :| the |n^{th}| outcome
|P(x_n) :| the probability of the |n^{th}| outcome
|B :| the initial bet
A game consists of spinning a roulette wheel. The initial bet for this game is |\$2.|
-
If the roulette wheel stops on the red section, the player wins |4| times their bet.
-
If the roulette wheel stops on the orange section, the player wins |4| times their bet.
-
If the roulette wheel stops on the purple section, the player wins |3| times their bet.
-
If the roulette wheel stops on the green section, the player wins |5| times their bet.
-
If the roulette wheel stops on the blue section, the player wins nothing.
Is this a fair game?
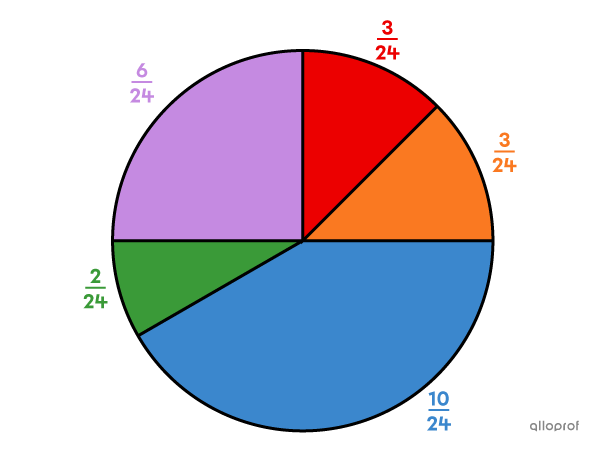
The mathematical expectation of the game must be calculated.
-
Red section: |4| times the bet |(4\times 2=\$8\ ).|
-
Orange section: |4| times the bet |(4\times 2=\$8\ ).|
-
Purple section: |3| times the bet |(3\times 2=\$6\ ).|
-
Green section: |5| times the bet |(5\times 2=\$10\ ).|
-
Blue section: The player wins nothing |(\$0\ ).|
We get the following table:
|
|X| |
|\$8\ | |
|\$8\ | |
|\$6\ | |
|\$10\ | |
|\$0\ | |
|---|---|---|---|---|---|
|
|P(X)| |
|\dfrac{3}{24}| |
|\dfrac{3}{24}| |
|\dfrac{6}{24}| |
|\dfrac{2}{24}| |
|\dfrac{10}{24}| |
We calculate the mathematical expectation:
||\begin{align}E &= \dfrac{3}{24} \times 8 + \dfrac{3}{24} \times 8 + \dfrac{6}{24} \times 6 + \dfrac{2}{24} \times 10 + \dfrac{10}{24} \times 0 - \color{#ec0000}{2}\\&=\dfrac{24}{24}+\dfrac{24}{24}+\dfrac{36}{24}+\dfrac{20}{24}-\color{#ec0000}2\\&=\dfrac{104}{24}-\color{#ec0000}2\\ &\approx 4.33-\color{#ec0000}{2}\\ &\approx \$2.33\ \end{align}||
Answer: If a player were to play several games, they would win an average of |\$2.33\ | per game. Since the expectation is greater than |0,| we can conclude that the game is in favour of the player. Therefore, the game is not fair.
Method 2: Remove the Bet From Each Outcome
If we remove the bet from each outcome, the mathematical expectation is calculated as follows.
|ME = P(x_1)(x_1-B) + P(x_2)(x_2-B) + \ldots + P(x_n)(x_n-B)|
where
|x_n :| the |n^{th}| outcome
|P(x_n) :| the probability of the |n^{th}| outcome
|B :| the initial bet
A game consists of spinning a roulette wheel. The initial bet for this game is |\$2.|
-
If the roulette wheel stops on the red section, the player wins |4| times their bet.
-
If the roulette wheel stops on the orange section, the player wins |4| times their bet.
-
If the roulette wheel stops on the purple section, the player wins |3| times their bet.
-
If the roulette wheel stops on the green section, the player wins |5| times their bet.
-
If the roulette wheel stops on the blue section, the player wins nothing.
Is this a fair game?
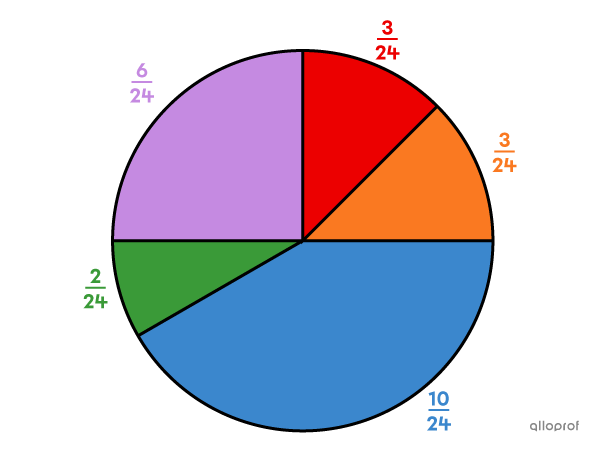
To calculate this, it is best to fill in a table indicating the result for each probability. In this table, the bet is subtracted.
-
Red section: |4| times the bet |(4\times 2-2=\$6\ ).|
-
Orange section: |4| times the bet |(4\times 2-2=\$6\ ).|
-
Purple section: |3| times the bet |(3\times 2-2=\$4\ ).|
-
Green section: |5| times the bet |(5\times 2-2=\$8\ ).|
-
Blue section: The player wins nothing |(0-2= -\$2\ ).|
|
|X| |
|\$6\ | |
|\$6\ | |
|\$4\ | |
|\$8\ | |
|-\$2\ | |
|---|---|---|---|---|---|
|
|P(X)| |
|\dfrac{3}{24}| |
|\dfrac{3}{24}| |
|\dfrac{6}{24}| |
|\dfrac{2}{24}| |
|\dfrac{10}{24}| |
We calculate the mathematical expectation.
||\begin{align} E &= \dfrac{3}{24} \times 6 + \dfrac{3}{24} \times 6 + \dfrac{6}{24} \times 4 + \dfrac{2}{24} \times 8 + \dfrac{10}{24} \times -2\\&=\dfrac{18}{24}+\dfrac{18}{24}+\dfrac{24}{24}+\dfrac{16}{24}-\dfrac{20}{24}\\&=\dfrac{56}{24}\\&\approx \$2.33\ \end{align}||
Answer: This game is not fair. In fact, it is in favour of the player since the mathematical expectation is greater than |0.|
The 2 formulas presented above always give the same results, since they are equivalent. Here is the proof.
||\begin{align}ME&=P(x_1)(x_1-B)+P(x_2)(x_2-B)+\ldots+P(x_n)(x_n-B)\\&=P(x_1)x_1-P(x_1)B+P(x_2)x_2-P(x_2)B+\ldots+P(x_n)x_n-P(x_n)B\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-P(x_1)B-P(x_2)B-\ldots-P(x_n)B\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-\boldsymbol{\color{#ec0000}{\big(P(x_1)+P(x_2)+\ldots+P(x_n)\big)}}B\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-\boldsymbol{\color{#ec0000}{(1)}}B\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-B\end{align}||