A random experiment is an experiment whose outcome depends entirely on chance and for which the possible outcomes are known.
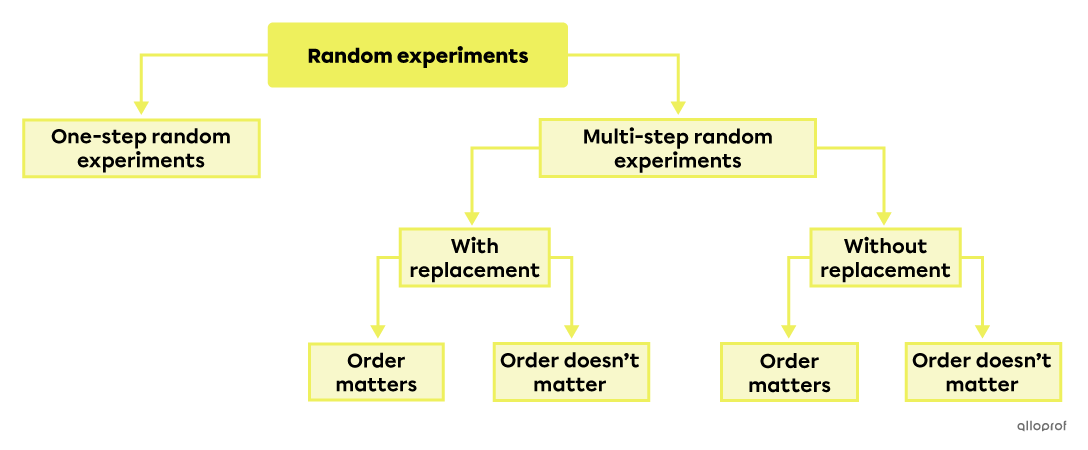
There are several types of random experiments. To enumerate and calculate probability, it is important to identify which type of problem it corresponds to by asking yourself 3 questions.
-
Are there multiple steps to the experiment?
-
If there are multiple steps, is the experiment with or without replacement?
-
If there are multiple steps, does the order of the outcomes matter or not?
The sample space of a one-step random experiment, or simple random experiment, is the enumeration of all the possible outcomes in braces. In this case, the probability of an event is expressed as the ratio of favourable outcomes to the total number of possible outcomes.
If a marble is randomly drawn from a bag containing |3| green marbles, |2| red marbles, and |1| blue marble, what is the probability of selecting a green marble?
There are |3| favourable outcomes (|3| green marbles) out of a total of |6| possible outcomes (|6| marbles in the bag).
||\begin{align}P(\text{Green marble})&=\dfrac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}\\&=\dfrac{3}{6}\end{align}||
Answer: The probability of randomly drawing a green marble is |\dfrac{3}{6},| or |\dfrac{1}{2}.|
If a marble is drawn randomly from a bag that contains |3| green marbles, |2| red marbles, and |1| blue marble, what is the probability of selecting a green or red marble?
There are |5| favourable outcomes (|3| green marbles and |2| red marbles) out of a total of |6| possible outcomes.
||\begin{align}P(\text{Green or Red marble})&=\dfrac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}\\&=\dfrac{3+2}{6}\\&=\dfrac{5}{6}\end{align}||
Answer: The probability of randomly drawing a red or green marble is |\dfrac{5}{6}.|
The sum of the probabilities of all simple events of a one-step random experiment is equal to |1.|
A marble is randomly chosen from a bag containing |3| green marbles, |2| red marbles, and |1| blue marble. The |3| simple events are: "drawing a green marble", "drawing a red marble" and "drawing a blue marble."
||\begin{align}P(\text{green})&=\dfrac{3}{6}\\P(\text{red})&=\dfrac{2}{6}\\P(\text{blue})&=\dfrac{1}{6}\\\end{align}||
If we add the probabilities of all the simple events, we indeed get |1.|
||\begin{align}P(\text{green})+P(\text{red})+P(\text{blue})&=\dfrac{3}{6}+\dfrac{2}{6}+\dfrac{1}{6}\\&=\dfrac{6}{6}\\&=1\end{align}||
A multi-step random experiment, also called a compound random experiment, is a series of random experiments performed one after the other.
To enumerate (list) all the possible outcomes of a multi-step random experiment, it is sometimes sufficient to multiply the number of possible outcomes at each step.
This is called the multiplication rule.
|\begin{gathered}\text{Number of}\\\text{possible}\\\text{outcomes}\end{gathered}=\begin{gathered}\text{Number of}\\\text{choices at}\\\text{step 1}\end{gathered}\times\begin{gathered}\text{Number of}\\\text{choices at}\\\text{step 2}\end{gathered}\times\ \dots|
To calculate the probability of a multi-step random experiment, simply multiply the probabilities of the different choices picked at each step. This is also the multiplication rule.
|P(A\ \text{followed by}\ B)=P(A)\times P(B)|
where
|P(A):| probability of 1st event
|P(B):| probability of 2nd event
Canadian postal codes are composed of numbers (N) and letters (L) in the following order: LNL NLN
-
The letters D, F, I, O, Q, and U are never used.
-
The letters W and Z are used, but never in 1st position.
Canada Post, whose postal code is K1A 0B1, estimates that there are currently |800\ 000| postal codes in use in Canada. What percentage of the total number of possible postal codes does this represent?
Canadian postal codes are composed of numbers (N) and letters (L) in the following order: LNL NLN
-
The letters D, F, I, O, Q, and U are never used.
-
The letters W and Z are used, but never in 1st position.
Canada Post, whose postal code is K1A 0B1, estimates that there are currently |800\ 000| postal codes in use in Canada. What percentage of the total number of possible postal codes does this represent?
To answer the question, first count the possible postal codes.
-
For the 1st letter, there are |18| possible choices (the |26| letters of the alphabet minus the |8| letters that are not used in 1st position).
-
For the 2nd and 3rd letters, there are |20| possible choices (the |26| letters of the alphabet minus the |6| letters that are not used).
-
For the 3 numbers, there are |10| possible choices.
|
L |
N |
L |
N |
L |
N |
|
|18| choices |
|10| choices |
|20| choices |
|10| choices |
|20| choices |
|10| choices |
According to the multiplication rule, we must multiply the possible choices at each step.
||18\times10\times20\times10\times20\times10=7\ 200\ 000||
There are |7\ 200\ 000| possible postal codes. What remains to be found is the percentage of postal codes currently in use.
||\begin{align}\dfrac{\text{Number of postal codes in use}}{\text{Number of possible postal codes}}&=\dfrac{800\ 000}{7\ 200\ 000}\\&=0.\overline{1}\\&\approx 11\ \% \end{align}||
Answer: In Canada, about |11\ \%| of the possible postal codes are in use.
In a multi-step random experiment, one should always consider if the experiment is with or without replacement and if the order matters or not.
A |6|-sided die is rolled twice in a row. What is the probability of rolling a |3| followed by a |4|?
A roll of a die is considered to be an experiment with replacement, because all |6| outcomes are still possible on the 2nd roll. Since we want a |3| followed by a |4,| we must take into account that the order matters.
The probability of rolling a |3| on the 1st throw is |\dfrac{1}{6}| and the probability of rolling a |4| on the 2nd throw is also |\dfrac{1}{6}.| The probabilities of each roll must be multiplied to find the probability of the event.
||P(\text{3 followed by a 4})=\dfrac{1}{6}\times \dfrac{1}{6} = \dfrac{1}{36}||
Answer: The probability of rolling a |3| followed by a |4| is |\dfrac{1}{36}.|
|3| cards are randomly chosen from a 52-card deck without replacing the chosen cards. What is the probability of getting (in order) |2| red cards and a black card?
The probability of getting a red card on the 1st pick is |\dfrac{26}{52},| or |\dfrac{1}{2}.| Since this is a random experiment without replacement, the probability of getting a red card on the 2nd pick is |\dfrac{25}{51}.| The probability of getting a black card on the last pick is |\dfrac{26}{50},| or |\dfrac{13}{25}.| The probabilities of each pick must be multiplied to find the probability of the event.
||P(R,R,N)=\dfrac{1}{2}\times \dfrac{25}{51}\times \dfrac{13}{25} = \dfrac{13}{102}||
Answer: The probability of picking |2| red cards followed by a black card is |\dfrac{13}{102}.|