En probabilités, il arrive qu’on doive faire certains choix par rapport à une expérience aléatoire impliquant des variables aléatoires quantitatives. Pour y arriver, on peut se servir de l’espérance mathématique.
L'espérance mathématique est la somme des produits des valeurs d'une variable aléatoire par leur probabilité.
En d'autres mots, l'espérance mathématique correspond à une moyenne pondérée des résultats d'une expérience aléatoire dans laquelle les facteurs de pondération sont les probabilités d'obtenir chacun des résultats.
L’espérance mathématique est habituellement utilisée dans le cadre de jeux de hasard. Dans ce contexte, l’espérance mathématique représente le gain moyen ou la perte moyenne que le joueur aurait s’il participait plusieurs fois au même jeu.
-
Lorsque l’espérance mathématique est égale à 0 |(E=0),| on dit que le jeu est équitable. Cela signifie que si on participe à ce jeu, en moyenne, on ne perd pas d’argent, mais on n’en gagne pas non plus. Ce jeu n'est donc pas à l'avantage du joueur ni des organisateurs du jeu.
-
Lorsque l’espérance mathématique est négative |(E<0),| cela signifie qu’en moyenne, le joueur perd de l’argent à chaque essai. Donc, le jeu est avantageux pour les organisateurs et est défavorable au joueur. Ce montant perdu à chaque essai est en moyenne égal à l’espérance mathématique.
-
Lorsque l’espérance mathématique est positive |(E>0),| cela signifie qu’en moyenne, le joueur gagne de l’argent à chaque essai. Donc, le jeu est désavantageux pour les organisateurs et favorable pour le joueur. Ce montant gagné à chaque essai est en moyenne égal à l’espérance mathématique.
Dans un contexte de jeux de hasard où il y a une mise de départ, on peut calculer l'espérance mathématique de plus d'une façon : soit on enlève la mise initiale à chaque résultat, soit on l'enlève à la fin seulement. Les 2 méthodes donnent exactement le même résultat. Il arrive également qu’il n’y ait pas de mise de départ.
Dans un calcul d'espérance mathématique, il est préférable de ne pas réduire les fractions, puisque cela facilite les additions de fractions.
Cynthia offre le pari suivant à Catherine.
« Pige une carte dans ce jeu de |52| cartes. Si tu piges un as, je te donne |5\ \$.| Si tu piges une figure, je te donne |2\ \$.| Si tu piges une autre carte que celles mentionnées, tu me donnes |1{,}50\ \$.| »
Est-ce que Catherine devrait accepter le pari proposé par Cynthia?
Pour répondre à cette question, Catherine doit calculer l’espérance mathématique du jeu. Si elle obtient un résultat négatif, elle ne devrait pas participer, puisqu’en moyenne, si elle joue à plusieurs reprises, elle perdra de l’argent. Au contraire, si l’espérance mathématique du jeu est positive, elle devrait accepter le pari, puisqu’en moyenne, elle gagnera de l’argent.
Le jeu de cartes contient |4| as sur un total de |52| cartes. La probabilité de piger un as est donc de |\dfrac{4}{52},| soit |\dfrac{1}{13}.| Cet évènement est associé à un gain de |5\ \$.|
Le jeu de cartes contient 12 figures (|4| valets, |4| dames et |4| rois) sur un total de |52| cartes. Cela correspond à une probabilité de |\dfrac{12}{52},| soit |\dfrac{3}{13}.| Cet évènement est associé à un gain de |2\ \$.|
Il y a |36| autres cartes (ni un as, ni un roi, ni une dame, ni un valet) dans un jeu de cartes. Cela correspond à une probabilité de |\dfrac{36}{52},| soit |\dfrac{9}{13}.| Cet évènement est associé à une perte de |1{,}50\ \$.|
On obtient le tableau suivant.
|
|X| |
|5\ \$| |
|2\ \$| |
|-1{,}50\ \$| |
|---|---|---|---|
|
|P(X)| |
|\dfrac{1}{13}| |
|\dfrac{3}{13}| |
|\dfrac{9}{13}| |
On peut maintenant calculer l'espérance mathématique.||\begin{align}E&= \dfrac{1}{13} \times 5 + \dfrac{3}{13} \times 2 + \dfrac{9}{13} \times -1{,}50\\&=\dfrac{5}{13}+\dfrac{6}{13}-\dfrac{13{,}5}{13}\\&=-\dfrac{2{,}5}{13}\\ &\approx -0{,}19\ \$ \end{align}||
Réponse : L’espérance mathématique est négative. En moyenne, Catherine perdrait de l’argent si elle acceptait le pari de Cynthia. Ainsi, elle ne devrait pas l’accepter.
Méthode 1 : Enlever la mise à la fin
Dans le cas où on enlève la mise à la fin, l’espérance mathématique se calcule de la façon suivante.
|E = P(x_1)x_1 + P(x_2)x_2 + \ldots P(x_n)x_n - M|
où
|x_n :| le |n^e| résultat
|P(x_n) :| la probabilité du |n^e| résultat
|M :| la mise initiale
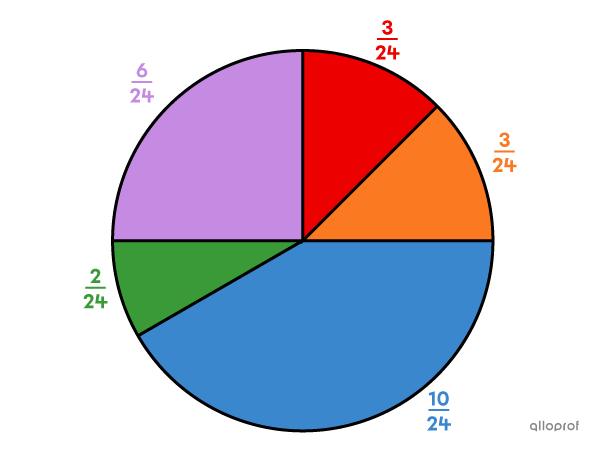
Un jeu consiste à faire tourner une roulette. La mise initiale à ce jeu est de |2\ \$.|
-
Si la roulette s'arrête sur la partie rouge, le joueur remporte |4| fois sa mise.
-
Si la roulette s'arrête sur la partie orange, le joueur remporte |4| fois sa mise.
-
Si la roulette s'arrête sur la partie mauve, le joueur remporte |3| fois sa mise.
-
Si la roulette s'arrête sur la partie verte, le joueur remporte |5| fois sa mise.
-
Si la roulette s'arrête sur la partie bleue, le joueur ne gagne rien.
Ce jeu est-il équitable?
Il faut déterminer l'espérance mathématique du jeu.
-
Section rouge : |4| fois la mise |(4\times 2=8\ \$).|
-
Section orange : |4| fois la mise |(4\times 2=8\ \$).|
-
Section mauve : |3| fois la mise |(3\times 2=6\ \$).|
-
Section verte : |5| fois la mise |(5\times 2=10\ \$).|
-
Section bleue : Le joueur ne gagne rien |(0\ \$).|
On obtient le tableau suivant.
|
|X| |
|8\ \$| |
|8\ \$| |
|6\ \$| |
|10\ \$| |
|0\ \$| |
|---|---|---|---|---|---|
|
|P(X)| |
|\dfrac{3}{24}| |
|\dfrac{3}{24}| |
|\dfrac{6}{24}| |
|\dfrac{2}{24}| |
|\dfrac{10}{24}| |
On calcule l'espérance mathématique.||\begin{align}E &= \dfrac{3}{24} \times 8 + \dfrac{3}{24} \times 8 + \dfrac{6}{24} \times 6 + \dfrac{2}{24} \times 10 + \dfrac{10}{24} \times 0 - \color{#ec0000}{2}\\&=\dfrac{24}{24}+\dfrac{24}{24}+\dfrac{36}{24}+\dfrac{20}{24}-\color{#ec0000}2\\&=\dfrac{104}{24}-\color{#ec0000}2\\ &\approx 4{,}33-\color{#ec0000}{2}\\ &\approx 2{,}33\ \$ \end{align}||
Réponse : S'il jouait plusieurs parties, un joueur gagnerait en moyenne |2{,}33\ \$| par partie. Puisque l’espérance est supérieure à |0,| on conclut que le jeu est favorable au joueur. Le jeu n’est donc pas équitable.
Méthode 2 : Enlever la mise à chaque résultat
Dans le cas où on enlève la mise à chaque résultat, l’espérance mathématique se calcule de la façon suivante.
|E = P(x_1)(x_1-M) + P(x_2)(x_2-M) + \ldots + P(x_n)(x_n-M)|
où
|x_n :| le |n^e| résultat
|P(x_n) :| la probabilité du |n^e| résultat
|M :| la mise initiale
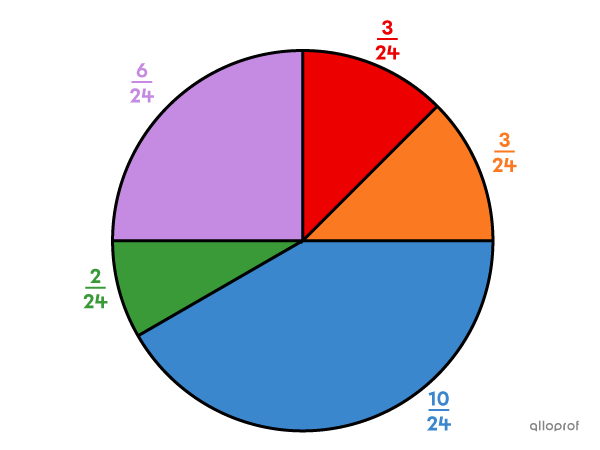
Le jeu consiste à faire tourner une roulette. La mise initiale est de |2\ \$.|
-
Si la roulette s'arrête sur la partie rouge, le joueur remporte |4| fois sa mise.
-
Si la roulette s'arrête sur la partie orange, le joueur remporte |4| fois sa mise.
-
Si la roulette s'arrête sur la partie mauve, le joueur remporte |3| fois sa mise.
-
Si la roulette s'arrête sur la partie verte, le joueur remporte |5| fois sa mise.
-
Si la roulette s'arrête sur la partie bleue, le joueur ne gagne rien.
Ce jeu est-il équitable?
Pour effectuer le calcul, il est préférable de remplir un tableau où on indique pour chaque probabilité le résultat obtenu. Dans ce tableau, on soustrait la mise.
-
Section rouge : |4| fois la mise moins la mise |(4\times 2-2=6\ \$).|
-
Section orange : |4| fois la mise moins la mise |(4\times 2-2=6\ \$).|
-
Section mauve : |3| fois la mise moins la mise |(3\times 2-2=4\ \$).|
-
Section verte : |5| fois la mise moins la mise |(5\times 2-2=8\ \$).|
-
Section bleue : Le joueur ne gagne rien et il perd sa mise |(0-2= -2\ \$).|
|
|X| |
|6\ \$| |
|6\ \$| |
|4\ \$| |
|8\ \$| |
|-2\ \$| |
|---|---|---|---|---|---|
|
|P(X)| |
|\dfrac{3}{24}| |
|\dfrac{3}{24}| |
|\dfrac{6}{24}| |
|\dfrac{2}{24}| |
|\dfrac{10}{24}| |
On calcule l'espérance mathématique.||\begin{align} E &= \dfrac{3}{24} \times 6 + \dfrac{3}{24} \times 6 + \dfrac{6}{24} \times 4 + \dfrac{2}{24} \times 8 + \dfrac{10}{24} \times -2\\&=\dfrac{18}{24}+\dfrac{18}{24}+\dfrac{24}{24}+\dfrac{16}{24}-\dfrac{20}{24}\\&=\dfrac{56}{24}\\&\approx 2{,}33\ \$ \end{align}||
Réponse : Ce jeu n’est pas équitable. En effet, il est favorable au joueur, puisque l’espérance mathématique est supérieure à |0.|
Les 2 formules présentées précédemment donnent toujours le même résultat, puisqu’elles sont équivalentes. En voici la preuve.||\begin{align}E&=P(x_1)(x_1-M)+P(x_2)(x_2-M)+\ldots+P(x_n)(x_n-M)\\&=P(x_1)x_1-P(x_1)M+P(x_2)x_2-P(x_2)M+\ldots+P(x_n)x_n-P(x_n)M\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-P(x_1)M-P(x_2)M-\ldots-P(x_n)M\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-\boldsymbol{\color{#ec0000}{\big(P(x_1)+P(x_2)+\ldots+P(x_n)\big)}}M\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-\boldsymbol{\color{#ec0000}{(1)}}M\\&=P(x_1)x_1+P(x_2)x_2+\ldots+P(x_n)x_n-M\end{align}||