In the Cartesian plane, a transformation matrix is a matrix that takes in the coordinates of an initial point to find the coordinates of its image under a given geometric transformation. It is important to be comfortable with multiplying matrices first.
Let an initial point be |(x,y)| and let the matrix |\begin{bmatrix}
a & b\\
c & d
\end{bmatrix}| be a transformation matrix.
The image of the point is |(x',y')| under the geometric transformation.
This image is calculated like so:
|\begin{bmatrix}
a & b\\
c & d
\end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}|
It is possible to perform various geometric transformations using matrices.
In a Cartesian plane, in order to perform a horizontal scaling by a factor |k|, apply the following transformation:
|\begin{bmatrix} k & 0 \\0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the initial point and |(x',y')| is the image of the point.
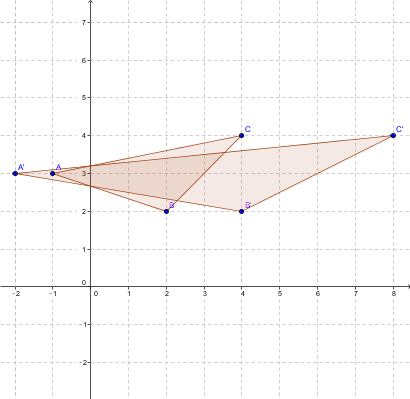
Let a triangle |ABC| have vertices |A=(-1,3), B=(2,2),| and |C=(4,4)|. We want to perform a horizontal scaling by a factor of |2|.
To find the vertices of the image of the figure, we perform the following calculations.
|\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} -1 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ 3 \end{bmatrix}=A'|
|\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 2 \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} = B'|
|\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 4 \\ 4 \end{bmatrix} = \begin{bmatrix} 8 \\ 4 \end{bmatrix} = C'|
This gives the following diagram.
In a Cartesian plane, in order to perform a vertical scaling by a factor |k|, apply the following transformation:
|\begin{bmatrix} 1 & 0 \\0 & k \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the initial point and |(x',y')| is the image.
Let a triangle |ABC| have vertices |A=(-1,3), B=(2,2),| and |C=(4,4)|. We want to vertically scale by a factor of |3|.
To find the vertices of the image of the figure, perform the following calculations.
|\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \times \begin{bmatrix} -1 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 \\ 9 \end{bmatrix}=A'|
|\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \times \begin{bmatrix} 2 \\ 2 \end{bmatrix} = \begin{bmatrix} 2 \\ 6 \end{bmatrix} = B'|
|\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \times \begin{bmatrix} 4 \\ 4 \end{bmatrix} = \begin{bmatrix} 4 \\ 12 \end{bmatrix} = C'|
This gives the following diagram.

In a Cartesian plane, in order to carry out a translation |t| with a vector |\overrightarrow{t}(a,b)|, we apply the following transformation:
|\begin{bmatrix} x+a \\ y+b \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the starting point and |(x',y')| is the image.
It is also possible to use the transformation matrix |\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ a & b \end{bmatrix}|. However, to use this matrix, it is necessary to form a new matrix where each row contains the coordinates of a point along with |1| in the last column.
|\begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ a & b \end{bmatrix} = \begin{bmatrix} x_{1'} & y_{1'} \\ x_{2'} & y_{2'} \\ x_{3'} & y_{3'} \end{bmatrix}|
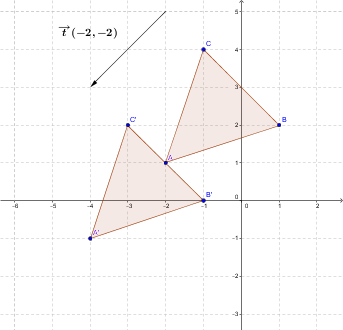
Consider the triangle |ABC| with vertices |A=(-2,1), B=(1,2),| and |C=(-1,4).| We want to translate the triangle using the vector |\overrightarrow{t}(-2,-2).|
The result is the following transformation:
|\begin{bmatrix} x-2 \\ y-2 \end{bmatrix}= \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the starting point and |(x',y')| is the image.
To find the vertices of the figure’s image, perform the following calculations.
|\begin{bmatrix} -2 -2 \\ 1 -2 \end{bmatrix} = \begin{bmatrix} -4 \\ -1 \end{bmatrix} =A'|
|\begin{bmatrix} 1 -2 \\ 2-2 \end{bmatrix} = \begin{bmatrix} -1 \\ 0 \end{bmatrix}=B'|
|\begin{bmatrix} -1 -2 \\ 4-2 \end{bmatrix} = \begin{bmatrix} -3 \\ 2 \end{bmatrix}=C'|
We get the same coordinates using the transformation matrix with 3 rows and 2 columns.
|\begin{bmatrix} -2 & 1 & 1 \\ 1 & 2 & 1 \\ -1 & 4 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ -2 & -2\end{bmatrix} = \begin{bmatrix} -4 & -1 \\ -1 & 0 \\ -3 & 2 \end{bmatrix}|
This gives the following diagram.
In a Cartesian plane, in order to perform a reflection |s| across the |x|-axis, denoted |s_x|, we apply the following transformation:
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the starting point and |(x',y')| is the image.
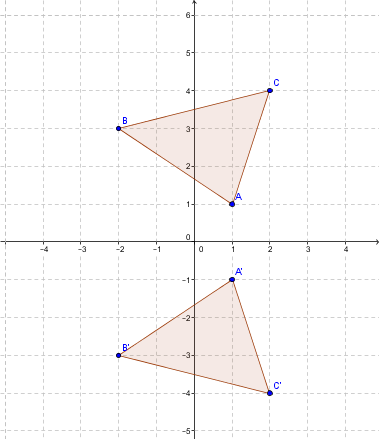
Consider the triangle |ABC| with vertices |A=(1,1), B=(-2,3),| and |C=(2,4)|. We want to reflect the triangle across the |x|-axis.
To find the vertices of the image of the figure, perform the following calculations.
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix}=A'|
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} -2 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ -3 \end{bmatrix}=B'|
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 2 \\ -4 \end{bmatrix} = C'|
This gives the following diagram.
In a Cartesian plane, in order to make a reflection |s| with respect to the |y|-axis, denoted |s_y|, apply the following transformation:
|\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the starting point and |(x',y')| is the image.
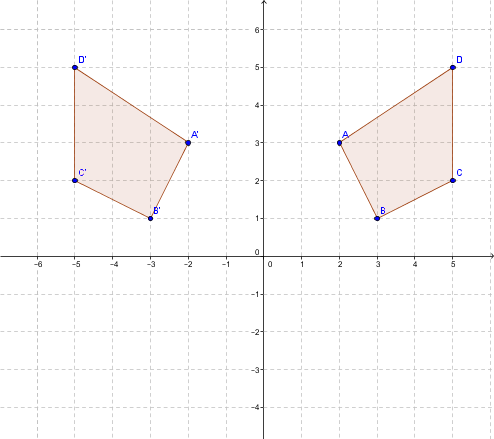
Consider the quadrilateral |ABCD| with vertices |A=(2,3)|, |B=(3,1)|, |C=(5,2)|, and |D=(5,5)|. We want to perform a reflection with respect to the |y|-axis.
To find the vertices of the image of the figure, perform the following calculations.
|\begin{bmatrix} -1 & 0 \\ 0 &1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ 3 \end{bmatrix}=A'|
|\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} -3 \\ 1 \end{bmatrix} = B'|
|\begin{bmatrix}-1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 5 \\ 2 \end{bmatrix} = \begin{bmatrix} -5 \\ 2 \end{bmatrix}=C'|
|\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 5 \\ 5 \end{bmatrix} = \begin{bmatrix} -5 \\ 5 \end{bmatrix} =D'|
This gives the following diagram.
In a Cartesian plane, in order to perform a rotation |r| by |90| degrees (counterclockwise) centred at the origin, we apply the following transformation:
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the initial point and |(x',y')| is the image.
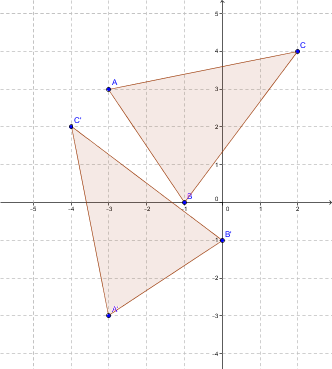
Consider the triangle |ABC| with vertices |A=(-3,3), B=(-1,0),| and |C=(2,4)|. We want to rotate it by |90| degrees around the origin counterclockwise.
To find the vertices of the image, perform the following calculations.
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} -3 \\ 3 \end{bmatrix} = \begin{bmatrix} -3 \\ -3 \end{bmatrix} =A'|
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} -1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ -1 \end{bmatrix} = B'|
|\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} -4 \\ 2 \end{bmatrix} = C'|
This gives the following diagram.
In a Cartesian plane, in order to perform a counterclockwise rotation |r| by |180| degrees centred at the origin, apply the following transformation:
|\begin{bmatrix} -1 & 0\\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the initial point and |(x',y')| is the image.
Consider the triangle |ABC| whose vertices are |A=(-4,1), B=(1,-2),| and |C=(3,3)|. We want to perform a counterclockwise rotation centred at the origin by |180| degrees.
To find the vertices of the image of the figure, perform the following calculations.
|\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} -4 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \end{bmatrix} =A'|
|\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 1 \\ -2 \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} = B'|
|\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} 3 \\ 3 \end{bmatrix} = \begin{bmatrix} -3 \\ -3 \end{bmatrix} = C'|
This gives the following diagram.
In a Cartesian plane, in order to perform a |270|-degree rotation (counterclockwise) centred at the origin, apply the following transformation:
|\begin{bmatrix} 0 & 1\\-1 & 0 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the initial point and |(x',y')| is the image.
Consider the triangle |ABC| with vertices |A=(-4,1), B=(1,-2)| and |C=(3,3)|. We want to perform a |270|-degree counterclockwise rotation centred at the origin.
To find the vertices of the image, perform the following calculations.
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} -4 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 4 \end{bmatrix} =A'|
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} 1 \\ -2 \end{bmatrix} = \begin{bmatrix} -2 \\ -1 \end{bmatrix} = B'|
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} 3 \\ 3 \end{bmatrix} = \begin{bmatrix} 3 \\ -3 \end{bmatrix} = C'|
This gives the following diagram.
In a Cartesian plane, in order to perform a dilation |h| by a scale factor |k| centred at the origin, apply the following transformation:
|\begin{bmatrix} k & 0 \\ 0 & k \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}| where |(x,y)| is the initial point and |(x',y')| is the image.
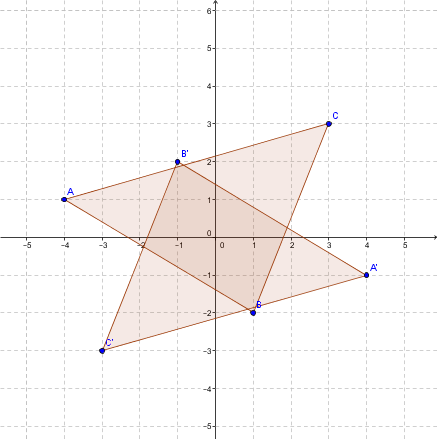
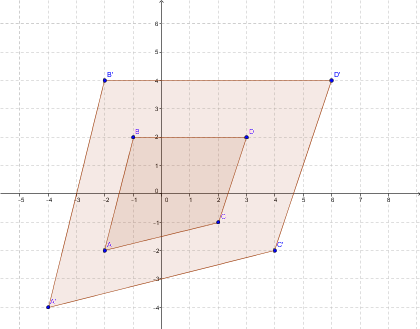
Consider the quadrilateral |ABCD| with vertices |A=(-2,-2)|, |B=(-1,2)|, |C=(2,-1)|, and |D=(3,2)|. We want to perform a dilation by a scale factor of |k=2| centred at the origin.
To find the vertices of the image of the figure, perform the following calculations.
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} -2 \\ -2 \end{bmatrix} = \begin{bmatrix} -4 \\ -4 \end{bmatrix}=A'|
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} -2 \\ 4 \end{bmatrix} = B'|
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 4 \\ -2 \end{bmatrix} = C'|
|\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \times \begin{bmatrix} 3 \\ 2 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \end{bmatrix} = D'|
This gives the following diagram.
To perform a composition of geometric transformations, apply each geometric transformation one after the other, starting from right to left. For example, with |s_x \circ s_y|, carry out |s_y| and then |s_x|.
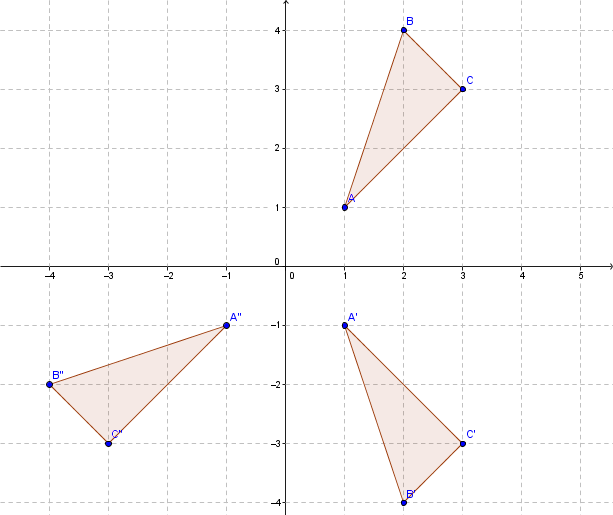
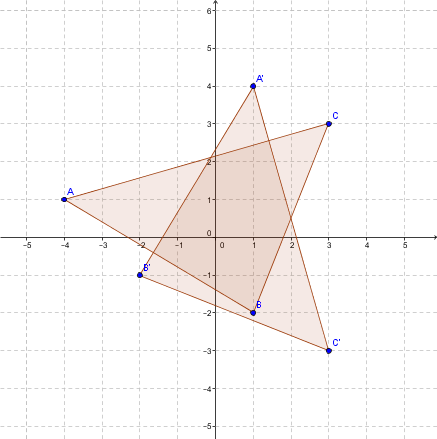
Consider the triangle |ABC| with vertices |A=(1,1), B=(2,4),| and |C=(3,3)|. We want to perform a reflection across the |x|-axis followed by a rotation by |270| degrees (counterclockwise) centred at the origin.
We write this as |r_{270} \circ s_x|.
Carry out the reflection across the |x|-axis.
|\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}|
Resulting in the following.
|A'=(1,-1), B'=(2,-4),| and |C'=(3,-3)|.
Next, perform the rotation of a 90° angle (counterclockwise) centred at the origin.
|\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \times \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x'' \\ y'' \end{bmatrix}|
We get the following coordinates.
|A''=(-1,-1), B''=(-4,-2)| et |C''=(-3,-3)|.
This gives the following diagram.