We can position real numbers in relation to each other by comparing them. They can be placed in ascending or descending order.
Putting numbers in ascending order means arranging them according to their value, from smallest to largest.
Putting numbers in descending order means arranging them according to their value, from largest to smallest.
Since the set of real numbers can be represented by a number line, this is very useful.
There are various methods of ordering real numbers. Here’s one.
Real numbers can be represented in several forms: decimal notation, fractional notation, radicals, etc.
To order them correctly, they must first be expressed in the same form. This is generally done using decimal notation.
-
Determine if the numbers should be placed in ascending or descending order.
-
Express each of the real numbers in decimal notation. Use a calculator if needed.
-
Keep as many decimal places as necessary when comparing numbers by rounding.
-
Position the numbers from Step 3 on a number line.
-
Place the numbers in the desired order, expressing them in their original form.
Place the following real numbers in descending order.||\dfrac{3}{4}\quad 0\quad -0.752\quad \sqrt[3]{2}\quad -\dfrac{\pi}{6}\quad \dfrac{6}{5}||
-
Determine if the numbers should be placed in ascending or descending order.
As mentioned in the problem statement, the numbers should be placed in descending order, or from largest to smallest. -
Express each of the real numbers in decimal notation. Use a calculator if needed.
||\begin{align}\dfrac{3}{4}&=0.75 & \sqrt[3]{2}&=1.259921...\\[4pt]
-\dfrac{\pi}{6}&=-0.523598... & \dfrac{6}{5}&=1.2\end{align}||
-
Keep as many decimal places as necessary when comparing numbers by rounding.
We will round to 3 decimal places. To compare the numbers more easily, it is helpful to add |\color{#ec0000}{0s}| so that all the decimal expansions have the same number of digits.
||\underbrace{0.75\color{#ec0000}{0}}_{\Large\frac{3}{4}}\quad \underbrace{0.\color{#ec0000}{000}}_{\large 0}\quad -\!0.752 \quad \underbrace{1.260}_{\large\sqrt[3]{2}}\quad \underbrace{-0.524}_{\Large-\frac{\pi}{6}}\quad \underbrace{1.2\color{#ec0000}{00}}_{\Large\frac{6}{5}}||
-
Position the numbers from Step 3 on a number line.
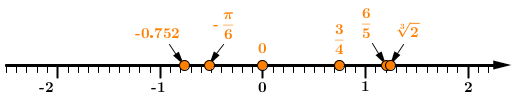
-
Place the numbers in the desired order, expressing them in their original form.
The following descending order is obtained:
||\sqrt[3]{2}\,>\,\dfrac{6}{5}\,>\,\dfrac{3}{4}\,>\,0\,>\,-\dfrac{\pi}{6}\,>\,-0.752||