La comparaison de nombres réels permet de situer ces nombres les uns par rapport aux autres. On peut alors les placer en ordre croissant ou en ordre décroissant.
Placer les nombres en ordre croissant revient à placer les nombres selon leur valeur, soit de la plus petite à la plus grande.
Placer les nombres en ordre décroissant revient à placer les nombres selon leur valeur, soit de la plus grande à la plus petite.
Comme l'ensemble des nombres réels peut être représenté par une droite numérique, cette dernière nous sera très utile.
Plusieurs méthodes permettent de placer des nombres réels en ordre. En voici une.
Les nombres réels peuvent être exprimés sous plusieurs formes: notation décimale, notation fractionnaire, radicaux, etc.
Pour pouvoir les mettre en ordre avec succès, il faut préalablement les exprimer tous sous la même forme. La forme qu'on privilégie généralement est la notation décimale.
-
Déterminer si on doit placer les nombres en ordre croissant ou décroissant.
-
Exprimer les nombres réels en notation décimale à l'aide de la calculatrice, au besoin.
-
Garder autant de décimales que nécessaire à la comparaison des nombres en arrondissant.
-
Positionner les nombres obtenus à l'étape 3 sur une droite numérique.
-
Placer les nombres dans l'ordre désiré en les exprimant sous leur forme initiale.
Placer en ordre décroissant les nombres réels suivants. ||\dfrac{3}{4}\quad 0\quad -0{,}752\quad \sqrt[3]{2}\quad -\dfrac{\pi}{6}\quad \dfrac{6}{5}||
-
Déterminer si on doit placer les nombres en ordre croissant ou décroissant
Tel que mentionné dans l'énoncé, les nombres doivent être placés en ordre décroissant, c'est-à-dire du plus grand au plus petit.
-
Exprimer les nombres réels en notation décimale à l'aide de la calculatrice, au besoin
||\begin{align}\dfrac{3}{4}&=0{,}75 & \sqrt[3]{2}&=1{,}259\,921...\\[4pt] -\dfrac{\pi}{6}&=-0{,}523\,598... & \dfrac{6}{5}&=1{,}2\end{align}||
-
Garder autant de décimales que nécessaire à la comparaison des nombres en arrondissant
Nous garderons 3 décimales. Afin de bien comparer les nombres, il est aussi conseillé d'ajouter des |\color{#ec0000}{0}| afin que toutes les parties décimales contiennent le même nombre de chiffres.
||\underbrace{0{,}75\color{#ec0000}{0}}_{\Large\frac{3}{4}}\quad \underbrace{0{,}\color{#ec0000}{000}}_{\large 0}\quad -\!0{,}752 \quad \underbrace{1{,}260}_{\large\sqrt[3]{2}}\quad \underbrace{-0{,}524}_{\Large-\frac{\pi}{6}}\quad \underbrace{1{,}2\color{#ec0000}{00}}_{\Large\frac{6}{5}}||
-
Positionner les nombres obtenus à l'étape 3 sur une droite numérique
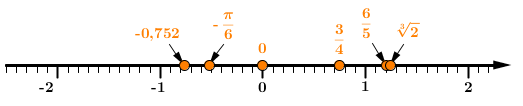
-
Placer les nombres dans l'ordre désiré en les exprimant sous leur forme initiale.
On obtient l'ordre décroissant suivant.
||\sqrt[3]{2}\,>\,\dfrac{6}{5}\,>\,\dfrac{3}{4}\,>\,0\,>\,-\dfrac{\pi}{6}\,>\,-0{,}752||