The set of real numbers, represented by the symbol |\mathbb{R},| includes all positive and negative numbers, rational or not, including the number |0.| These numbers can be written using finite or infinite decimal expansions.
The set of real numbers corresponds to the union of rational numbers |(\mathbb{Q})| and irrational numbers |(\mathbb{Q'}| or |\mathbb{R}\backslash\mathbb{Q}).| Therefore, any number that is included in the set of rational numbers or in the set of irrational numbers is also part of the set of real numbers.||\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}'||
The number line is a representation of the set of real numbers. Every real number can be represented by a point on the number line. This is why the number line, which is continuous from |-\infty| to |+\infty,| is also called the real number line.
All the numbers located on the following number line are real numbers.

Using interval notation, the set of real numbers can be represented as follows:||x \in \mathbb R \ \text{if}\ x \in\, ]\!-\!\infty,+\infty[||
The sum of any real number and its opposite is always equal to |0.|
In other words, opposite numbers have the same absolute value but opposite signs.
-
The opposite of an integer
The opposite of |-6| is |6.| -
The opposite of a rational number in fractional notation
The opposite of |\dfrac{1}{3}| is |-\dfrac{1}{3}.| -
The opposite of a rational number in decimal notation
The opposite of |1.\overline{3}| is |-1.\overline{3}.| -
The opposite of an irrational number
The opposite of |-\sqrt{2}| is |\sqrt{2}.|
The product of any real number and its reciprocal is always equal to |1.|
To determine the reciprocal of a number, first write it in fractional notation, and then invert the numerator and denominator.
Note: |0| is the only number with no reciprocal.
-
The reciprocal of a natural number
The reciprocal of |6| is |\dfrac{1}{6}.| -
The reciprocal of an integer
The reciprocal of |-12| is |\dfrac{1}{-12}=-\dfrac{1}{12}.| -
The reciprocal of a rational number in fractional notation
The reciprocal of |\dfrac{7}{10}| is |\dfrac{10}{7}.| -
The reciprocal of a rational number in decimal notation
The reciprocal of |-0.2| is |\dfrac{1}{-0.2} =\dfrac{1}{-\frac{2}{10}}=\dfrac{10}{-2} =-5.| -
The reciprocal of an irrational number
The reciprocal of |\dfrac{\sqrt{5}}{2}| is |\dfrac{2}{\sqrt{5}}.| To avoid leaving a square root in the denominator, we rationalize the resulting fraction.||\dfrac{2}{\sqrt{5}} = \dfrac{2}{\sqrt{5}} \times \dfrac{\sqrt{5}}{\sqrt{5}} = \dfrac{2\sqrt{5}}{5}||
The real number set |(\mathbb{R})| is composed of 2 subsets: rational numbers |(\mathbb{Q})| and irrational numbers |(\mathbb{Q'}| or |\mathbb{R}\backslash\mathbb{Q}).|||\mathbb{R}=\mathbb{Q}\cup\mathbb{Q}'||
Furthermore, since the natural numbers |(\mathbb{N})| are included in the set of integers |(\mathbb{Z}),| which is included in the set of rational numbers |(\mathbb{Q}),| which is itself included in the set of real numbers |(\mathbb{R}),| the following relationship exists:||\mathbb N\subset\mathbb Z\subset \mathbb Q\subset \mathbb R.||
Here's a diagram showing the position of all the number sets in the set of real numbers.
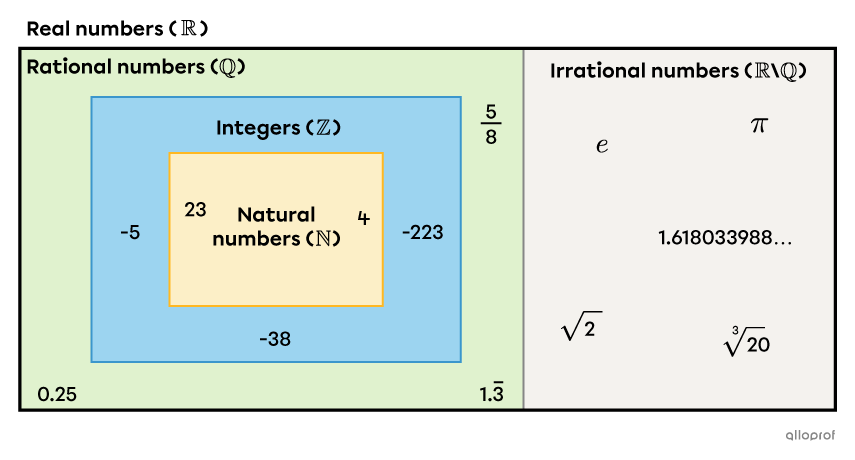
-
The number |4| is a natural number. It is also an integer. What's more, it's considered a rational number, since it can be written as a ratio of integers: |\dfrac{4}{1}.| Therefore, since |4| is a natural number, an integer and a rational number, it's automatically a real number.
-
The number |\pi| is neither a natural number, nor an integer, nor a rational number. However, because it is an irrational number, it is also a real number.
-
Using appropriate notation, we obtain the following:||\begin{align}4&\in\mathbb{N}\subset\mathbb Z\subset \mathbb Q\subset \mathbb R\\[3pt] \pi&\in\mathbb{Q}'\subset\mathbb{R}\end{align}.||
-
We denote |\mathbb{R}^*| the set of real numbers excluding the number |0.|
-
We denote |\mathbb {R}_+| the set of positive real numbers.
-
We denote |\mathbb {R}_-| the set of negative real numbers.
-
These notations can be combined. For example, we denote |\mathbb{R}^*_-| the set of negative real numbers excluding the number |0.|
To order real numbers, it's useful to convert them into decimal notation.
All the numbers we work with in high school are real numbers.
However, beyond real numbers, there is another set of numbers, called complex numbers |(\mathbb{C}).| These are based on the existence of an imaginary number, denoted |i,| which is defined as follows: |i=\sqrt{-1}.| Because the square root of a negative number has no real solution, |i| is said to be an imaginary number. Complex numbers are widely used in physics and most branches of engineering.