Amongst the solids, we distinguish between those whose faces are uniquely polygons (polyhedrons) and those with at least one face that is a curved surface (non-polyhedrons).
A solid must have a key characteristic to be considered a polyhedron.
A polyhedron is a solid whose surfaces are all formed by polygons. In other words, a polyhedron does not have any curved surfaces.
The following are examples of polyhedrons.
A polyhedron can be constructed with a combination of triangles, squares, rectangles, rhombuses, or any other closed polygon. The polygons used to construct a polyhedron can be used to identify and classify it.
Due to the simplicity of their construction, these polyhedrons are seen most often in everyday life.
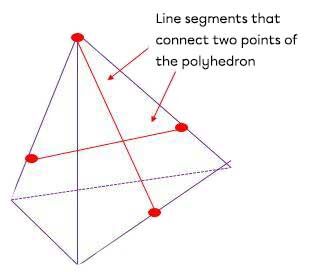
A convex polyhedron is a solid in which all line segments that join any two points on its surface are entirely included in the portion of space it occupies.
In other words, there are no hollows or cavities visible on its surfaces.
In the following triangular pyramid, the two line segments are on the surface or inside the polyhedron.
A non-convex polyhedron is a solid with a base, or bases, that are non-convex polygons.
A non-convex polyhedron is a solid in which at least one line segment that connects two points on its surface lies outside of the portion of space occupied by the polyhedron.
In other words, there is a hollow or a cavity inside the polyhedron.
Note in the following example, when the two red points of the non-convex pentagonal prism connect, the line segment formed is located on the outside of the prism.
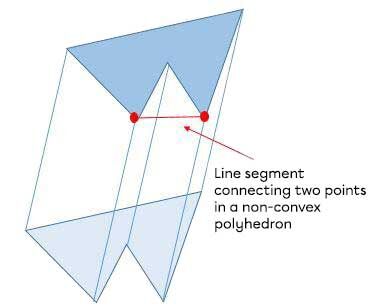
The same is true for a polyhedron when a section inside is removed.
Here, notice that the red line segment passes through the portion of the prism that is empty.
A regular polyhedron is formed by the repeated use of a single regular polygon.
A regular polyhedron is made up of regular isometric (congruent) polygons, where each vertex has the same number of edges connecting it.
Regular polyhedrons are also categorized into two families based on whether or not they are convex.
Regular polyhedrons with the following characteristics are considered Platonic solids.
-
All of the faces are regular isometric (congruent) polygons.
-
None of its faces intersect, except at the edges.
-
The same number of faces meet at each vertex.
The most common regular polyhedrons are the cube and tetrahedron.
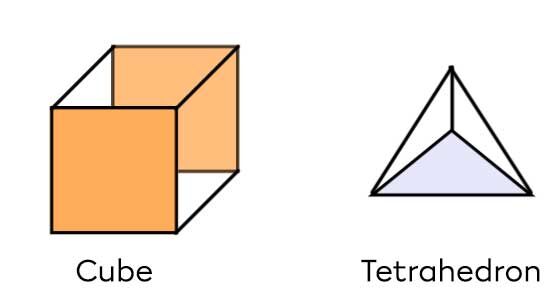
In summary, the cube is made up of six squares which are isometric (congruent) and three squares meet at each vertex. The tetrahedron is formed by four isometric (congruent) equilateral triangles and three triangles meet at each vertex.
Plato's Polyhedra
The other three Platonic solids are the octahedron, dodecahedron, and icosahedron.
Kepler-Poinsot Polyhedra
This polyhedron family is made up of regular non-convex polyhedrons. Click here to learn more about them.
Polyhedrons can be right or oblique.
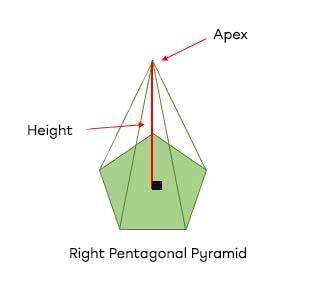
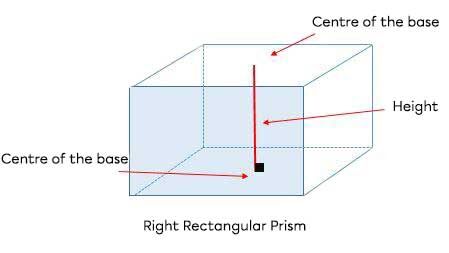
A right polyhedron is a polyhedron whose height from the centre of one base joins the centre of the other base (for prisms) or the apex (for pyramids).
In other words, it's a polyhedron that stands up vertically at a right angle.
Example with a base and an apex
Example with two bases
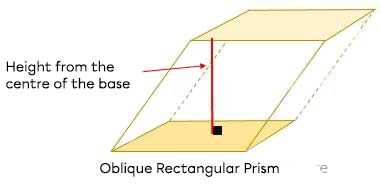
A polyhedron is oblique if this perpendicular characteristic is not present.
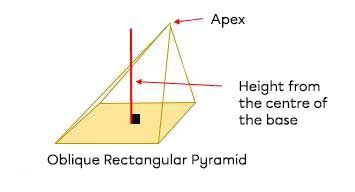
An oblique polyhedron is a polyhedron whose height from the centre of one base does not connect the centre of the other base (for prisms) or the apex (for pyramids).
It is difficult to build large buildings that are oblique because the support structures needed to hold the building are very difficult to implement.
Example with a base and an apex
Example with two bases