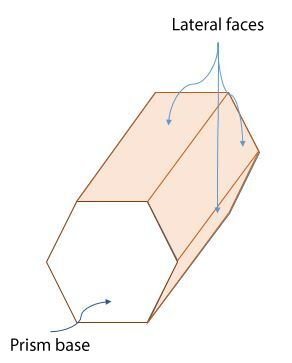
A prism is a solid that can resemble a desktop computer tower or a chocolate bar. To be considered a prism, a solid must have certain essential characteristics.
A prism is a polyhedron with two congruent and parallel faces called bases, and quadrilaterals forming the lateral faces.
Of course, there are several types of prisms including the two shown below.
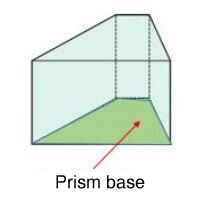
Prisms are named according to the polygons that form their bases. Thus, prisms with bases that are triangles are called "triangular prisms"; prisms with bases that are pentagons are called "pentagonal prisms", and so on.

When a prism has a base that is a quadrilateral, the name of the quadrilateral is used. Looking at the prisms shown in the example above, the one on the left is called a "trapezoidal prism" since the base is a trapezoid.
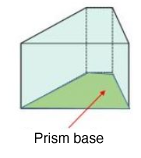
In order to clearly define prisms, it is important to analyse both the polygons used to form the bases as well as the height in relation to these bases.
A regular prism is a right prism with bases that are regular, congruent polygons.
Moreover, it can be deduced that the quadrilaterals forming the lateral faces are congruent rectangles.
Regular triangular prism
Since the triangle is equilateral, and therefore a regular polygon, this right prism is also a regular prism.
Regular pentagonal prism
In this case, we indicate that all the pentagon’s sides have the same measurement. Since this is a regular pentagon, then the right prism will also be regular.

However, there are other qualifiers to describe prisms.
Generally, right prisms are popular in everyday life because they are easy and practical to construct. However, some architects and artists occasionally experiment with constructions made with oblique prisms.
A right prism is a prism where the height from the centre of one of its bases meets the centre of the other.
When walking around town or in the countryside, different prisms can be observed serving as homes or places of work.
Prism with an unique base
In the case of the National Bank of Canada Tower, the building was constructed perfectly vertical (right prism), but with an unusual base.
Whether for aesthetic reasons or due to the forces of nature, some buildings are not built as straight prisms. In this case, they are referred to as oblique prisms.
The height of an oblique prism does not connect the centre of the two bases. In other words, the bases are identical, but they are not “aligned”.
In the following example, notice that the bases (the floor and the roof) are parallel and identical, but they are not “aligned”.
When the proper methods and materials are used, buildings that resemble oblique prisms can be just as strong as those that are right prisms.
In the previous drawing, note that the two green bases are identical, but their centres (|\color{red}{\text{red}}| and |\color{blue}{\text{blue}}| points) are not aligned. Thus, it is an oblique prism.