In the following interactive animation, experiment with the values of the parameters |a,| |b,| |h,| and |k| of the rational function in standard form and observe how they affect the function’s properties. Afterwards, read the concept sheet to learn more about the function and its properties.
|
Property |
Characteristics |
|---|---|
|
Domain |
|x \in \mathbb{R}^*| (mathematically) |
|
Range |
|y \in \mathbb{R}^*| (mathematically) |
|
|y|-intercept |
The graph of the basic rational function does not cross the |y|-axis. Therefore, there is no |y|-intercept. |
|
|x|-intercept |
The curve does not cross the |x|-axis. Therefore, there is no |x|-intercept. |
|
Variation: increasing and decreasing intervals |
The basic rational function decreases over all |x| with the exception of |x=0,| where it is undefined. |
|
Positive and negative intervals |
The basic rational function is positive when |x>0| and negative when |x<0|. |
|
Asymptotes |
There are two asymptotes: |y=0| and |x=0|. |
|
Vertex |
There is no vertex. |
|
Extrema |
There are no extrema. |
|
Axis of symmetry |
The rational function has two axes of symmetry. |
|
Property |
Characteristics of the function in standard form |
|---|---|
|
Equation |
|f(x) = \dfrac{a}{b(x - h)} + k| or |f(x) = \dfrac{a_1}{x - h} + k| |
|
Equation of the asymptotes |
|x = h| and |y = k| |
|
Domain |
|dom f = \mathbb{R} \backslash \left\{h\right\}| |
|
Range |
|range f = \mathbb{R} \backslash \left\{k\right\}| |
|
|y|-intercept |
If it exists, it is equal to |f(0).| |
|
|x|-intercept |
If it exists, it is the value of |x| when |f(x) = 0.| |
|
Variation: increasing and decreasing intervals |
|
|
Positive and negative intervals of |f| |
Using the equation of the function, for an interval of |x,| the function |f| is :
|
|
Extrema |
No extrema (unless the context limits the domain). |
Determine the properties of the rational function with equation |f(x)=\displaystyle - \frac{1}{2(x+1)}+2.|
To begin, it may be useful to draw a graph of the function.
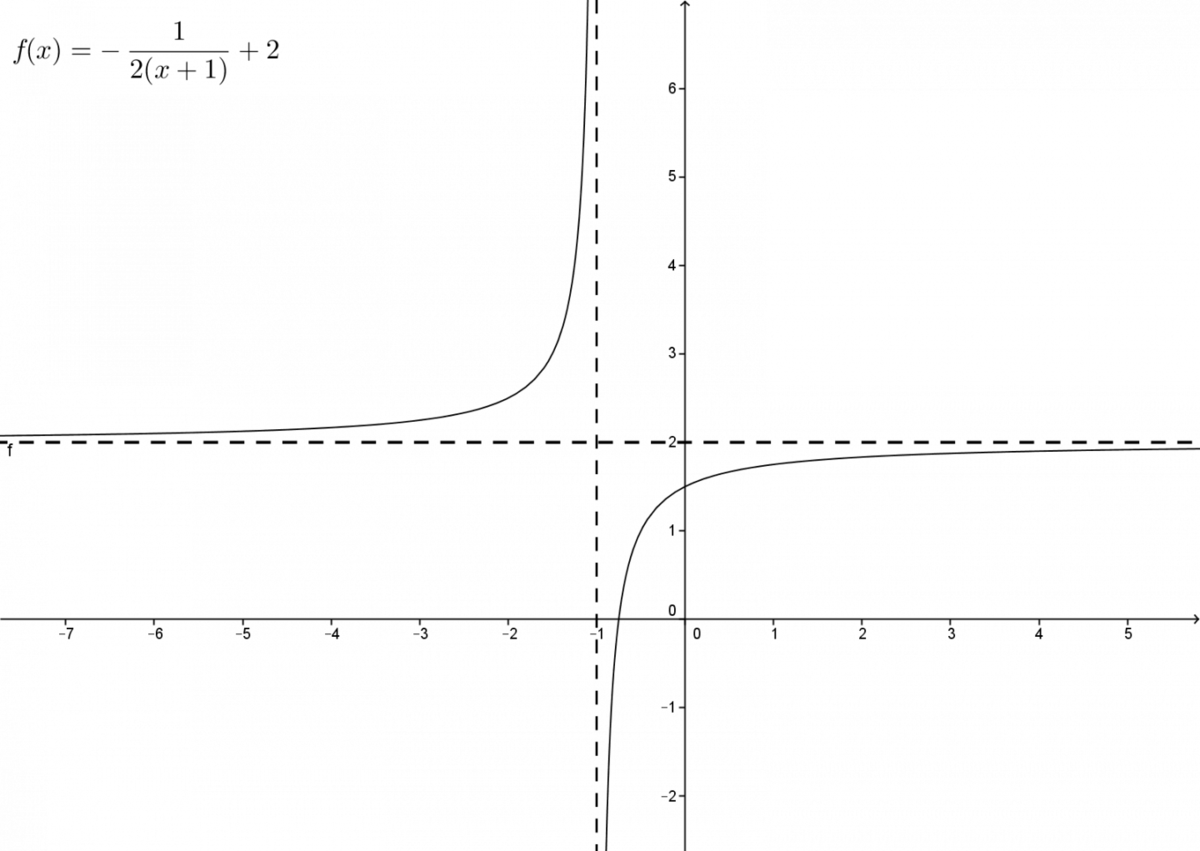
-
The domain of the function is |\mathbb{R} \backslash \lbrace -1 \rbrace|. The value of |-1| makes the denominator of the fraction zero, so it must be eliminated from the domain.
-
The range of the function is |\mathbb{R} \backslash \lbrace 2 \rbrace|.
-
The |y|-intercept is calculated by replacing |x| with |0| in the equation. ||\begin{align}f(0) &= -\dfrac{1}{2(0+1)}+2\\f(0) &= -\dfrac{1}{2} + 2\\f(0) &= \dfrac{3}{2}\end{align}|| Thus, the |y|-intercept of the function is equal to |\dfrac{3}{2}|.
-
The |x|-intercept is calculated by replacing |f(x)| with |0| and then isolating |x|. ||\begin{align}0 &= - \dfrac{1}{2(x+1)}+2\\-2 &= -\dfrac{1}{2(x+1)}\\-2 \times 2(x+1) &= -1\\-4x -4 &= -1\\-4x &= 3\\x &= -\dfrac{3}{4}\end{align}|| Thus, the |x|-intercept of the function is equal to |\dfrac{3}{4}|.
-
Intervals: Since |a| and |b| have opposite signs, the function increases over its entire domain, i.e., over |\mathbb{R} \backslash \lbrace -1 \rbrace|.
-
This function has no extrema.
-
Positive and negative intervals : from the |x|-intercept and the graph, it is clear that:
-
the function is positive on |(-\infty,-1)\ \cup\ (-\dfrac{3}{4}, +\infty)|;
-
the function is negative on |(-1, -\dfrac{3}{4}]|.
It is important to exclude the value of |x=-1|.
-
-
The axes of symmetry of the function are given by the equations |y=(x+1)+2,| which is equivalent to |y=x+3| and |y=-(x+1)+2,| which is equivalent to |y=-x+1.|
-
The equations of the asymptotes are |x=-1| and |y=2.|
-
The centre of the hyperbola is located at the point |(h,k)=(-1,2).|