Rational functions include a fraction with an independent variable |(x)| in the denominator.
The rational function is often associated with the inverse variation function (inversely proportional situation). In reality, the inverse variation function is a special set of rational functions.
The rule of an inverse variation function is |f(x)=\dfrac{k}{x}| where |x \neq 0.|
The basic form of a rational function is the following.
||f(x)=\dfrac{1}{x}|| where |x \neq 0|
The graph of the basic rational function is composed of 2 curves, called hyperbolas, which approach the 2 axes without touching them.
-
One curve intersects the point |(1,1),| and the other the point |(-1,-1).|
-
The domain is |\mathbb{R}\backslash \{0\}.|
-
The range is |\mathbb{R}\backslash \{0\}.|
-
The function is decreasing over the interval |]-\infty,0[,| and then over the interval |]0,+\infty[.|
-
The basic function has no |y|-intercept or zero.
-
The function has no maximum or minimum.
-
The function has 2 perpendicular asymptotes: |x=0| and |y=0.|
-
The function is negative over the interval |]-\infty,0[| and is positive over the interval |]0,+\infty[.|

The transformed rational function can be written in 2 different ways.
The standard form
||f(x)=\dfrac{a}{b(x-h)}+k|| where |b\neq 0|
The general form
||f(x)=\dfrac{a_1 x+b_1}{a_2 x+b_2}|| where |a_2 \neq 0|
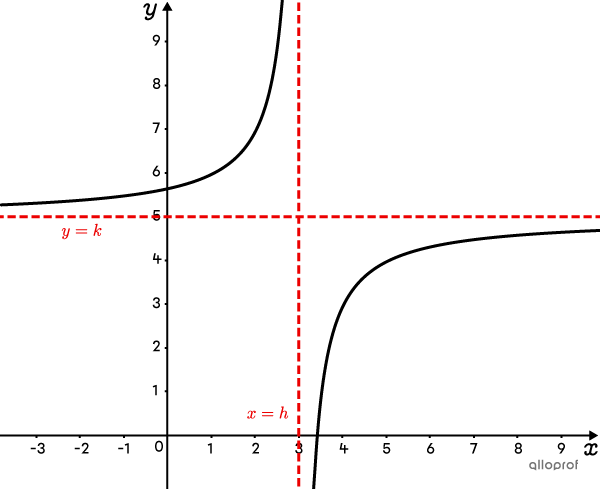
The graph of the transformed rational function is composed of 2 curves, called hyperbolas, which approach the 2 asymptotes without touching them.
-
The domain is |\mathbb{R}\backslash \{h\}.|
-
The range is |\mathbb{R}\backslash \{k\}.|
-
When |ab>0,| the function is decreasing over the interval |]-\infty,h[,| and then over the interval |]h,+\infty[.|
-
When |ab<0,| the function is increasing over the interval |]-\infty,h[,| and then over the interval |]h,+\infty[.|
-
The function has a |y|-intercept if |h\neq 0| and a zero if |k \neq 0.|
-
The function has no maximum or minimum.
-
The function has 2 perpendicular asymptotes: |x=h| and |y=k.|
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction rationnelle de façon interactive, consulte la MiniRécup suivante.
