Dans l'animation interactive suivante, tu peux modifier les paramètres |a,| |b,| |h| et |k| de la fonction rationnelle en forme canonique et observer leurs effets sur les propriétés de la fonction. Après cette exploration, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions concernant les propriétés de la fonction.
| PROPRIÉTÉS | CARACTÉRISTIQUES |
|---|---|
| Domaine | |x \in \mathbb{R}^*| (modèle mathématique) |x \in \mathbb{R}_+| (modèle mathématique pour les problèmes quotidiens) |
| Codomaine | |y \in \mathbb{R}^*| (modèle mathématique) |y \in \mathbb{R}_+| (modèle mathématique pour les problèmes quotidiens) |
| Ordonnée à l'origine | Le graphique de la fonction rationnelle de base ne coupe pas l'axe des |y|. Il n'y a donc pas d'ordonnée à l'origine. |
| Abscisse à l'origine (zéro de la fonction) |
La courbe ne coupe pas l'axe des |x|. Il n'y a donc pas d'abscisse à l'origine. |
| Croissance et décroissance | La fonction rationnelle de base est décroissante pour tous les |x| à l'exception de |x=0,| où elle n'est pas définie. |
| Signes | La fonction rationnelle de base est positive pour |x>0| et négative pour |x<0|. |
| Asymptotes | Il y a deux asymptotes : |y=0| et |x=0|. Leur point de rencontre constitue le centre de l'hyperbole. |
| Sommet (centre de l'hyperbole) |
Il n'y a pas de sommet. Le point important de la fonction rationnelle de base est l'intersection des deux asymptotes. C'est le centre de l'hyperbole. Pour la fonction de base, c'est le point |(0,0)|. |
| Extrémums | Il n'y a pas d'extrémums. |
| Axe de symétrie | La fonction rationnelle possède deux axes de symétrie. L'équation de ces axes sont |y=-x| et |y=x|. Il s'agit de la droite diagonale des quadrants |I| et |III| et de la diagonale des quadrants |II| et |IV|. |
| Propriétés | Caractéristiques de la fonction en forme canonique |
|---|---|
|
Règle |
|f(x) = \dfrac{a}{b(x - h)} + k| ou |f(x) = \dfrac{a_1}{x - h} + k| |
|
Équations des asymptotes |
|x = h| et |y = k| |
|
Domaine |
|\text{dom }(f) = \mathbb{R} \backslash \left\{h\right\}| |
|
Image |
|\text{ima }(f) = \mathbb{R} \backslash \left\{k\right\}| |
|
Ordonnée à l'origine |
Si elle existe, c'est la valeur de |f(0).| |
|
Abscisse à l'origine |
S'il existe, c'est la valeur de |x| pour laquelle |f(x) = 0.| |
|
Croissance et décroissance |
|
|
Signe de la fonction |f| |
Selon l'équation de la fonction, pour un intervalle de valeurs de |x,| la fonction |f| est :
|
|
Extrémums |
Pas d'extrémums (sauf si le contexte limite le domaine). |
Détermine les propriétés de la fonction rationnelle d'équation |f(x)=\displaystyle - \frac{1}{2(x+1)}+2.|
Au départ, il peut être utile de tracer une esquisse graphique de la fonction.
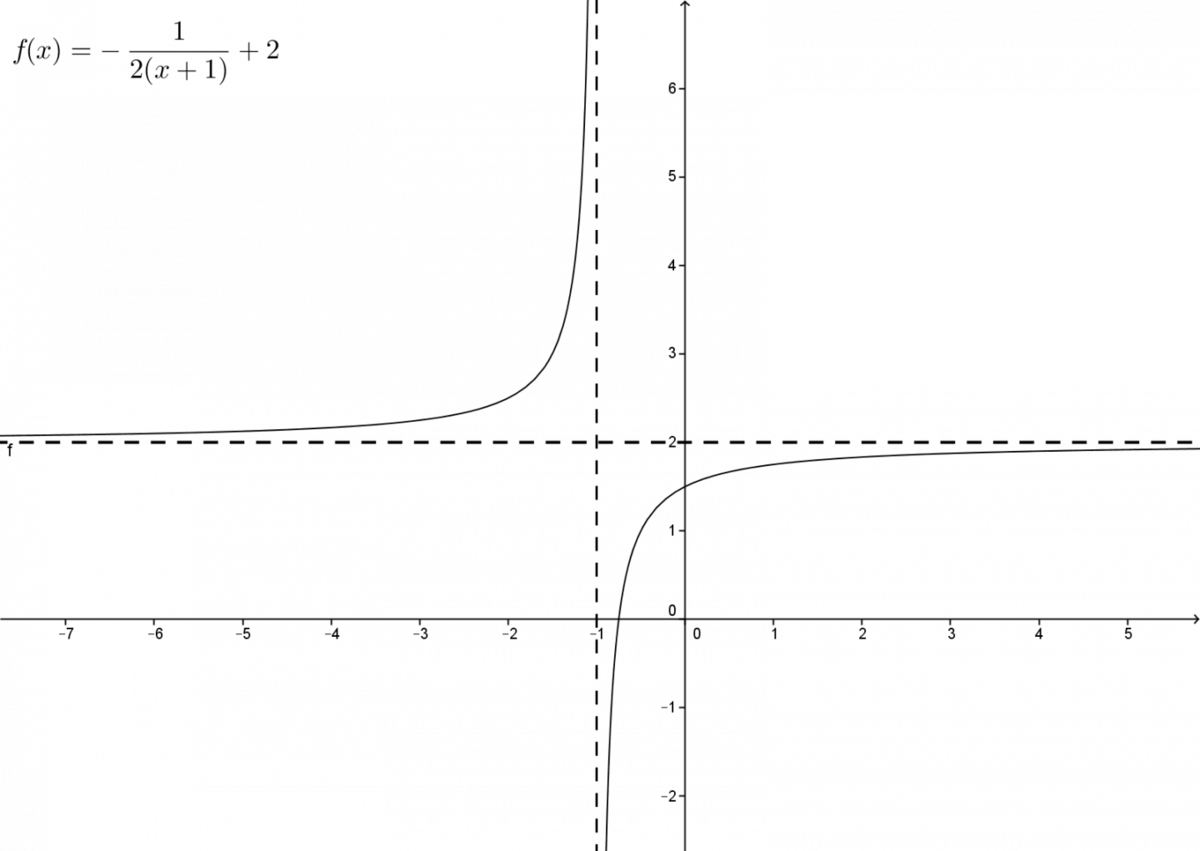
-
Le domaine de la fonction est |\mathbb{R} \backslash \lbrace -1 \rbrace|. La valeur de |-1| est celle qui annulerait le dénominateur de la fraction, il faut donc l'éliminer.
-
L'image de la fonction est |\mathbb{R} \backslash \lbrace 2 \rbrace|.
-
L'ordonnée à l'origine se calcule en remplaçant |x| par 0 dans notre équation. ||\begin{align}f(0) &= -\dfrac{1}{2(0+1)}+2\\f(0) &= -\dfrac{1}{2} + 2\\f(0) &= \dfrac{3}{2}\end{align}|| Ainsi, l'ordonnée à l'origine de la fonction vaut |\displaystyle \frac{3}{2}|.
-
L'abscisse à l'origine se calcule en remplaçant |f(x)| par 0 et en isolant ensuite |x|. ||\begin{align}0 &= - \dfrac{1}{2(x+1)}+2\\-2 &= -\dfrac{1}{2(x+1)}\\-2 \times 2(x+1) &= -1\\-4x -4 &= -1\\-4x &= 3\\x &= -\dfrac{3}{4}\end{align}|| Ainsi, l'abscisse à l'origine de la fonction vaut |\displaystyle - \frac{3}{4}|.
-
Variation : Comme |a| et |b| sont de signes contraires, la fonction est croissante sur tout son domaine, c'est-à-dire sur |\mathbb{R} \backslash \lbrace -1 \rbrace|.
-
Cette fonction ne possède aucun extrémum.
-
Signes : en utilisant l'abscisse à l'origine et le graphique, on peut déterminer que :
-
La fonction est positive sur |]-\infty,-1[\ \cup\ [-\frac{3}{4}, +\infty[|.
-
La fonction est négative sur |]-1, -\frac{3}{4}]|.
Il est important d'exclure des intervalles la valeur de |x=-1|.
-
-
Les axes de symétrie de la fonction sont donnés par l'équation |y=(x+1)+2,| qui est équivalente à |y=x+3| et par l'équation |y=-(x+1)+2,| qui est équivalente à |y=-x+1.|
-
Les équations des asymptotes sont |x=-1| et |y=2.|
-
Le centre de l'hyperbole est situé au point |(h,k)=(-1,2).|