In the following animation, experiment with modifying the parameters |a,| |h,| and |k| of the quadratic (or second-degree polynomial) function. Observe the effects of the parameters on the function’s properties. Afterwards, consult the concept sheet for all of the details concerning the properties of the function.
|
Properties |
Quadratic function in the form ||f(x)=ax^2\quad \text{where}\quad a<0||The curve of the function opens downwards. |
Quadratic function in the form ||f(x)=ax^2\quad \text{where}\quad a>0||The curve of the function opens upwards. |
|---|---|---|
|
Domain |
The set of real numbers |\mathbb{R}| |
The set of real numbers |\mathbb{R}| |
|
Range |
The set of negative real numbers, |\mathbb{R}_-|. |
The set of positive real numbers, |\mathbb{R}_+|. |
|
|y|-Intercept |
|0| |
|0| |
|
|x|-intercept |
|0| |
|0| |
|
Vertex |
The point |(0,0)| |
The point |(0,0)| |
|
Variation or increasing and decreasing intervals |
The function increases over |]\text{-}\infty, 0]| and decreases over |[0,\infty[.| |
The function increases over |[0,\infty[| and decreases over |]\text{-}\infty,0].| |
|
Extrema |
The function has a maximum of |y=0.| |
The function has a minimum of |y=0.| |
|
Signs or positive and negative intervals |
The function is negative over all its domain. |
The function is positive over all its domain. |
|
Axis of symmetry |
The equation of the axis of symmetry is |x=0.| |
The equation of the axis of symmetry is |x=0.| |
|
Properties |
General form |f(x)=ax^2+bx+c| |
Standard form |f(x)=a(x-h)^2+k| |
Factored form |f(x)=a(x-x_1)(x-x_2)| |
|---|---|---|---|
|
Domain |
|x \in \mathbb{R}| |
||
|
Range |
If |a>0|, then |\left[\frac{4ac-b^2}{4a}, +\infty \right[.| If |a<0|, then |\left]-\infty, \frac{4ac-b^2}{4a}\right].| |
If |a>0|, then If |a<0|, then |
If |a>0|, then |\left[\frac{-a(x_2-x_1)^2}{4},+\infty\right[.| If |a<0|, then |\left] - \infty, \frac{-a(x_2-x_1)^2}{4} \right].| |
|
|y|-intercept |
|f(0)=c| |
|f(0)=ah^2+k| |
|f(0)=ax_1x_2| |
|
Replace |x| with |0| in the equation and calculate the value of |y.| |
|||
|
|x|-intercept |
If |b^2-4ac>0|, then there are 2 distinct zeroes. If |b^2-4ac=0|, then there is only one zero. If |b^2-4ac<0|, then there is no zero. Zeroes can be found by factorization or the quadratic formula. ||x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}|| |
If |a| and |k| have different signs, then there will be 2 distinct zeroes. If |k=0|, then there will be a single zero. If |a| and |k| have the same sign, then there will be no zero. Zeroes can be found by replacing |f(x)| by |0| and isolating |x|, or by using the following formula. ||x_{1,2}=h\pm \sqrt{\frac{-k}{a}}|| |
The zeroes are |x_1| and |x_2.| |
|
Vertex |
|\left(\dfrac{-b}{2a},\dfrac{4ac-b^2}{4a}\right)| |
|(h,k)| |
|\left(\dfrac{x_1+x_2}{2},\dfrac{-a(x_2-x_1)^2}{4}\right)| |
|
Variation or Increasing and decreasing intervals |
If |a>0|, then If |a<0|, then |
If |a>0|, then If |a<0|, then |
If |a>0|, then If |a<0|, then |
|
Extrema |
|\dfrac{4ac-b^2}{4a}| A maximum if |a<0.| A minimum if |a>0.| |
|k| A maximum if |a<0.| A minimum if |a>0.| |
|\dfrac{-a(x_2-x_1)^2}{4}| A maximum if A minimum if |
|
Signs or Positive and negative intervals |
If |a>0| and there is only one or no zero, then the function is positive for all |x.| If |a<0| and there is only one or no zero, then the function is negative for all |x.| If |a>0| and there are 2 zeroes, then the function is negative for the interval between the 2 zeroes and positive for all other |x.| If |a<0| and there are 2 zeroes, then the function is positive for the interval between the 2 zeroes and negative for all other |x.| |
||
|
Axis of symmetry |
|x=\dfrac{-b}{2a}| |
|x=h| |
|x=\dfrac{x_1+x_2}{2}| |
|
Asymptotes |
There are no asymptotes. |
||
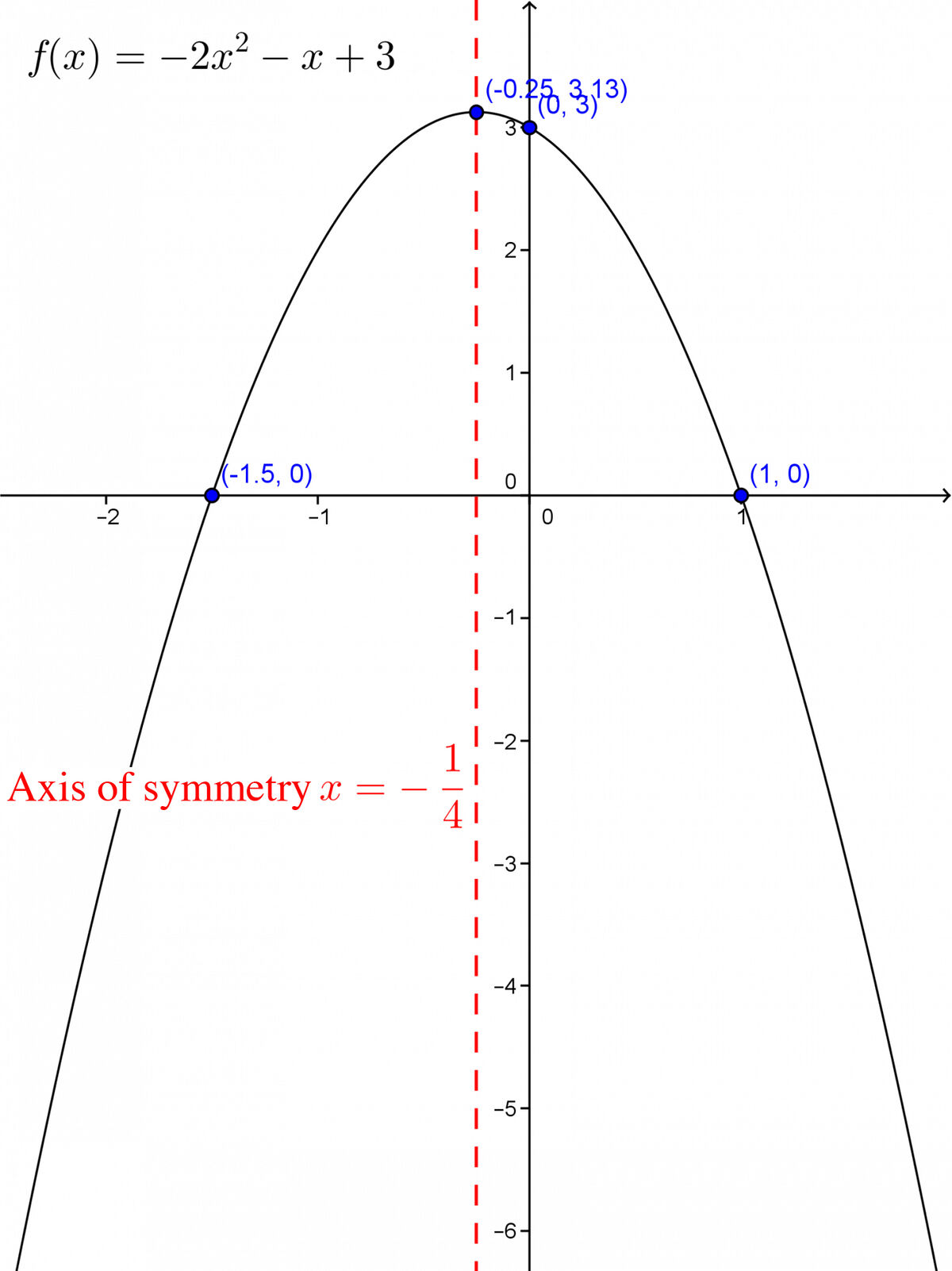
Determine the properties of the quadratic function with the following equation. ||f(x)=-2x^2-x+3||
It may be useful to sketch the graph of the function.
-
The domain of the function is |\mathbb{R}.|
-
To determine the range of the function, it is important to know if the function opens upwards or downwards, as well as the |y|-coordinate of the vertex, i.e. the parameter |k.|
The parameter |a| is negative, so the graph of the function must open downwards (the graph confirms it). As for the parameter |k,| it must be calculated using the formula |\displaystyle k=\frac{4ac-b^2}{4a}.| ||\begin{align} k &= \frac{4ac-b^2}{4a} \\ &= \frac{4(-2)(3) - (-1)^2}{4 (-2)} \\ &= \frac{-25}{-8} \\ &= \frac{25}{8} \end{align}||Thus, the range of the function is |]-\infty, \frac{25}{8}].| -
The |y|-intercept of a quadratic polynomial function in general form is given by the value of |c|, which here is |3.|
-
The zeroes of the function can be found using the quadratic formula. ||\begin{align} x_{1,2} &= \frac{-b \pm\sqrt{b^2-4ac}}{2a} \\ &= \frac{-(-1) \pm \sqrt{(-1)^2-4 (-2) (3)}}{2 (-2)} \\ &= \frac{1 \pm \sqrt{25}}{-4} \end{align}||Next, separate the formula into two answers: one using the |+| and the other using the |-.| |x_1| will be one zero and |x_2| will be the other zero. ||\begin{align} x_1 &= \frac{1+\sqrt{25}}{-4} = \frac{1+5}{-4}=\frac{6}{-4}=- \frac{3}{2} \\ x_2 &= \frac{1-\sqrt{25}}{-4}=\frac{1-5}{-4}=\frac{-4}{-4}=1 \end{align}||Thus, the two zeroes of the function are |-\dfrac{3}{2}| and |1.|
-
To find the parameter |h,| calculate the average between the two zeroes. ||h = \frac{-\frac{3}{2}+1}{2} = \frac{-\frac{1}{2}}{2}=-\frac{1}{4}||Thus, the coordinates of the vertex are |\displaystyle (h,k)=\left( -\frac{1}{4}, \frac{25}{8} \right).|
-
The variation or intervals of increase and decrease: the function increases over |\left]-\infty, -\dfrac{1}{4}\right]| and decreases over |\left[-\dfrac{1}{4}, +\infty\right[.|
-
Extrema: because the graph of the function opens downwards, it has a maximum of |y=k,| i.e. the maximum is |\dfrac{25}{8}.|
-
The sign or the positive and negative intervals: the function is positive over |[-1.5, 1]| and negative over |]-\infty, -1.5] \cup [1, +\infty[.|
-
The equation of the axis of symmetry is |x=h.| Therefore, |x= -\dfrac{1}{4}.|
To determine the properties of a quadratic function, it is easiest to work with the standard form of the function.
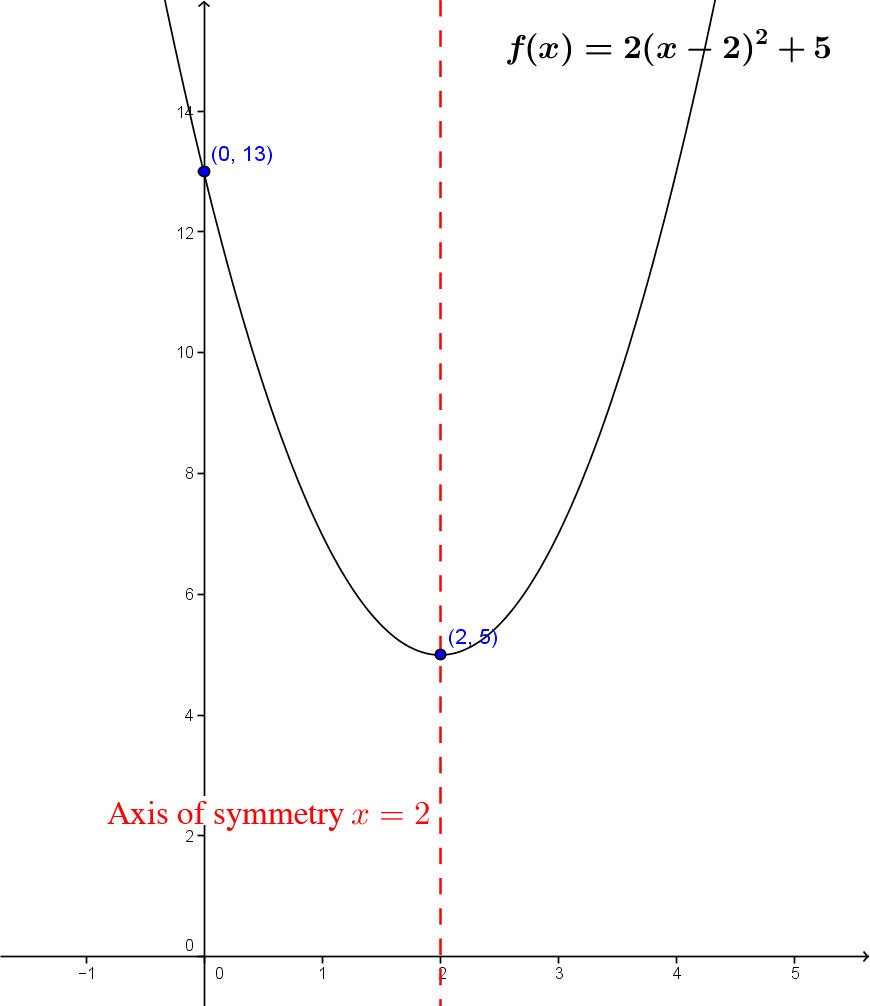
Determine the properties of the quadratic function with the following equation. ||f(x)=2(x-2)^2+5||
It may be useful to sketch a graph of the function.
-
The domain of the function is |\mathbb{R}.|
-
The function’s range is |[5, +\infty[.| The function opens upwards, because its parameter |a| is positive and the |y|-coordinate of the vertex is |5.|
-
The |y|-intercept of a quadratic function in standard form is calculated by replacing |x| with |0.|||\begin{align} f(x) &= 2(x-2)^2+5 \\ f(0) &= 2(0-2)^2+5 \\ f(0) &= 2(-2)^2+5 \\ f(0) &= 2 (4) + 5 \\ f(0) &= 8 + 5 \\ f(0) &= 13 \end{align}|| The |y|-intercept of the function is |13.|
-
Since the |y|-coordinate of the vertex is greater than |0| and the graph of the function opens upwards, the function does not have a zero.
-
The coordinates of the vertex are |(h,k)=(2,5).|
-
The function increases over |[2, +\infty[| and decreases over |]-\infty,2].|
-
Since the graph of the function is open upwards, it has a minimum when |y=k|, i.e. the minimum is |5.|
-
As the range of the function is always positive |([5, + \infty[),| the function is positive over its entire domain.
-
The equation of the axis of symmetry is |x=h.| Thus, |x=2.|
Pour valider ta compréhension des propriétés des fonctions de façon interactive, consulte la MiniRécup suivante :
