Dans l'animation suivante, tu peux modifier les paramètres |a,| |h| et |k| de la fonction polynomiale de degré 2 et observer leurs effets sur les propriétés de la fonction. Après cette exploration, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions concernant les propriétés de la fonction.
| Propriétés | Fonction quadratique sous la forme ||f(x)=ax^2\quad \text{où}\quad a<0||La courbe de la fonction est ouvert vers le bas. | Fonction quadratique sous la forme ||f(x)=ax^2\quad \text{où}\quad a>0||La courbe de la fonction est ouvert vers le haut. |
|---|---|---|
|
Domaine |
L'ensemble des nombres réels |\mathbb{R}| |
L'ensemble des nombres réels |\mathbb{R}| |
|
Codomaine |
L'ensemble des nombres réels négatifs, |\mathbb{R}_-| |
L'ensemble des nombres réels positifs, |\mathbb{R}_+| |
|
Ordonnée à l'origine |
Elle vaut |0.| |
Elle vaut |0.| |
|
Abscisse à l'origine |
Elle vaut |0.| |
Elle vaut |0.| |
|
Sommet |
C'est le point |(0,0).| |
C'est le point |(0,0).| |
|
Croissance et décroissance |
La fonction est croissante sur |]\text{-}\infty, 0]| et elle est décroissante sur |[0,\infty[.| |
La fonction est croissante sur |[0,\infty[| et elle est décroissante sur |]\text{-}\infty,0].| |
|
Extrémums |
Elle possède un maximum en |y=0.| |
Elle possède un minimum en |y=0.| |
|
Signes |
La fonction est négative sur l'ensemble de son domaine. |
La fonction est positive sur l'ensemble de son domaine. |
|
Axe de symétrie |
L'axe de symétrie a pour équation |x=0.| |
L'axe de symétrie a pour équation |x=0.| |
| Propriétés |
Forme générale |f(x)=ax^2+bx+c| |
Forme canonique |f(x)=a(x-h)^2+k| |
Forme factorisée |f(x)=a(x-x_1)(x-x_2)| |
|---|---|---|---|
|
Domaine |
|x \in \mathbb{R}| |
||
|
Codomaine |
Si |a>0|, alors |\left[\frac{4ac-b^2}{4a}, +\infty \right[| Si |a<0|, alors |\left]-\infty, \frac{4ac-b^2}{4a}\right]| |
Si |a>0|, alors Si |a<0|, alors |
Si |a>0|, alors |\left[\frac{-a(x_2-x_1)^2}{4},+\infty\right[| Si |a<0|, alors |\left] - \infty, \frac{-a(x_2-x_1)^2}{4} \right]| |
|
Ordonnée à l'origine |
|f(0)=c| |
|f(0)=ah^2+k| |
|f(0)=ax_1x_2| |
|
Il faut remplacer |x| par |0| dans l'équation et calculer la valeur du |y.| |
|||
|
Abscisse(s) à l'origine |
Si |b^2-4ac>0|, alors il y a 2 zéros distincts. Si |b^2-4ac=0|, alors il y a un seul zéro. Si |b^2-4ac<0|, alors il n'y a pas de zéro. Les zéros peuvent être trouvés à l'aide de la factorisation ou avec la formule quadratique : ||x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}|| |
Si |a| et |k| sont de signes différents, alors il y aura 2 zéros distincts. Si |k=0|, alors il y aura un seul zéro. Si |a| et |k| sont du même signe, alors il n'y aura pas de zéro. Les zéros peuvent être trouvés en remplaçant |f(x)| par |0| et en isolant |x| ou en utilisant la formule suivante : ||x_{1,2}=h\pm \sqrt{\frac{-k}{a}}|| |
Les zéros sont : |
|
Sommet |
|\left(\dfrac{-b}{2a},\dfrac{4ac-b^2}{4a}\right)| |
|(h,k)| |
|\left(\dfrac{x_1+x_2}{2},\dfrac{-a(x_2-x_1)^2}{4}\right)| |
|
Croissance et décroissance |
Si |a>0|, alors Si |a<0|, alors |
Si |a>0|, alors Si |a<0|, alors |
Si |a>0|, alors Si |a<0|, alors |
|
Extrémums |
|\dfrac{4ac-b^2}{4a}| C'est un maximum si |a<0.| C'est un minimum si |a>0.| |
|k| C'est un maximum si |a<0.| C'est un minimum si |a>0.| |
|\dfrac{-a(x_2-x_1)^2}{4}| C'est un maximum si C'est un minimum si |
|
Signes |
Si |a>0| et qu'il y a un seul ou aucun zéro, alors la fonction est positive pour tous les |x.| Si |a<0| et qu'il y a un seul ou aucun zéro, alors la fonction est négative pour tous les |x.| Si |a>0| et qu'il y a 2 zéros, alors la fonction est négative pour l'intervalle des |x| compris entre les 2 zéros et elle est positive pour le reste des |x.| Si |a<0| et qu'il y a 2 zéros, alors la fonction est positive pour l'intervalle des |x| compris entre les 2 zéros et elle est négative pour le reste des |x.| |
||
|
Axe de symétrie |
|x=\dfrac{-b}{2a}| |
|x=h| |
|x=\dfrac{x_1+x_2}{2}| |
|
Asymptotes |
Il n'y a pas d'asymptote. |
||
Déterminez les propriétés de la fonction polynomiale du second degré d'équation ||f(x)=-2x^2-x+3.||
Il peut être utile de tracer le graphique de la fonction.
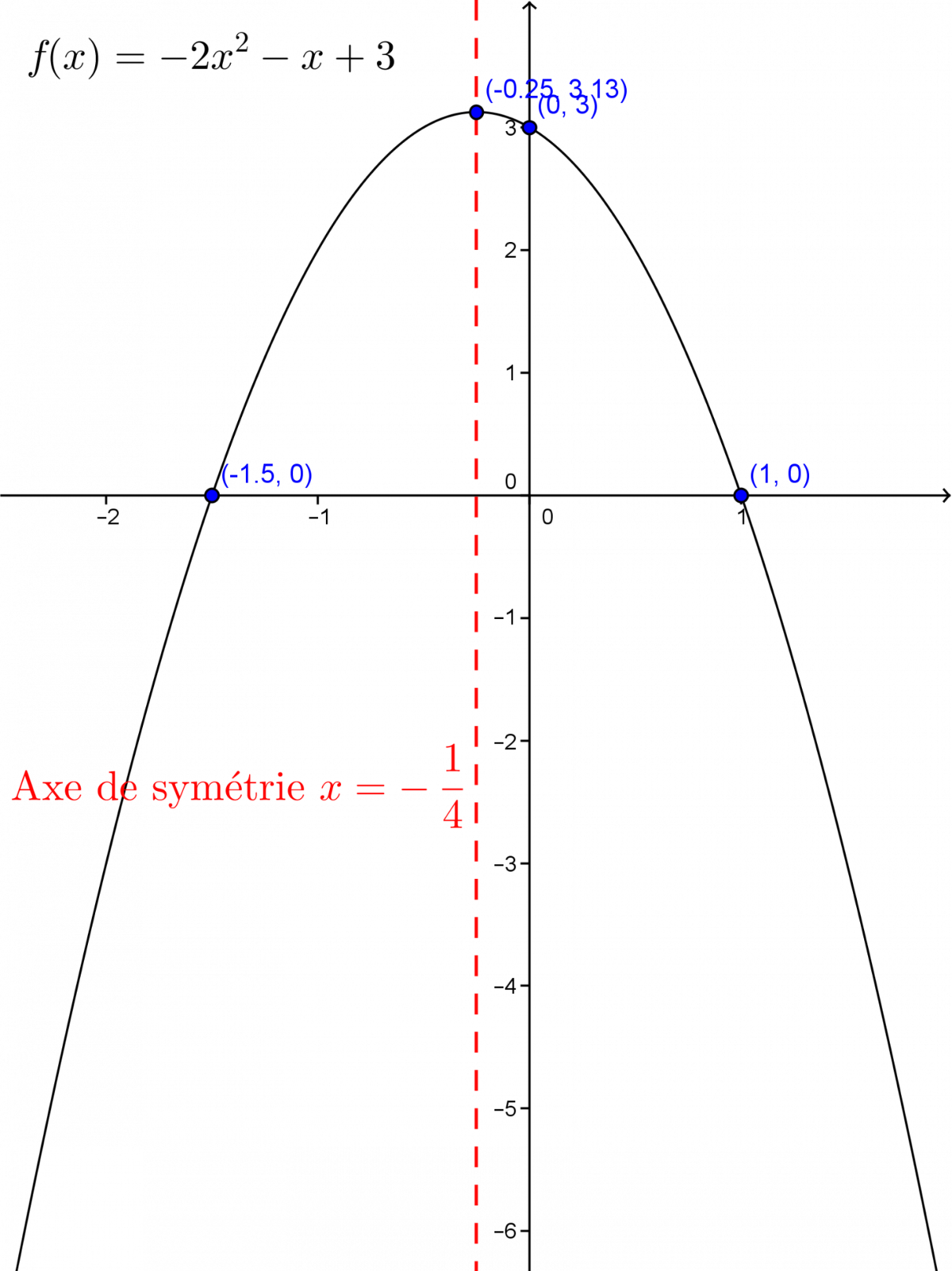
-
Le domaine de la fonction est |\mathbb{R}.|
-
Pour déterminer l'image de la fonction, il faut savoir si le graphique de cette dernière est ouvert vers le haut ou vers le bas et il faut connaitre l'ordonnée de son sommet, c'est-à-dire le paramètre |k.|
Le paramètre |a| étant négatif, le graphique de la fonction est ouvert vers le bas (le graphique le confirme). Pour ce qui est du paramètre |k,| il faut le calculer grâce à la formule |\displaystyle k=\frac{4ac-b^2}{4a}.| ||\begin{align} k &= \frac{4ac-b^2}{4a} \\ &= \frac{4(-2)(3) - (-1)^2}{4 (-2)} \\ &= \frac{-25}{-8} \\ &= \frac{25}{8} \end{align}||Ainsi, l'image de la fonction est |]-\infty, \frac{25}{8}].| -
L'ordonnée à l'origine d'une fonction polynomiale du second degré sous la forme générale étant donnée par la valeur de |c| vaut |3.|
-
On peut trouver les zéros de la fonction en utilisant la formule quadratique. ||\begin{align} x_{1,2} &= \frac{-b \pm\sqrt{b^2-4ac}}{2a} \\ &= \frac{-(-1) \pm \sqrt{(-1)^2-4 (-2) (3)}}{2 (-2)} \\ &= \frac{1 \pm \sqrt{25}}{-4} \end{align}||Rendu ici, il faut séparer la formule en deux parties : l'une utilisant le |+| et l'autre utilisant le |-.| |x_1| sera un zéro et |x_2| sera l'autre zéro. ||\begin{align} x_1 &= \frac{1+\sqrt{25}}{-4} = \frac{1+5}{-4}=\frac{6}{-4}=- \frac{3}{2} \\ x_2 &= \frac{1-\sqrt{25}}{-4}=\frac{1-5}{-4}=\frac{-4}{-4}=1 \end{align}||Ainsi, les deux zéros de la fonction ont pour valeurs |-\dfrac{3}{2}| et |1.|
-
Pour trouver le paramètre |h,| il suffit de calculer la moyenne entre les deux zéros. ||h = \frac{-\frac{3}{2}+1}{2} = \frac{-\frac{1}{2}}{2}=-\frac{1}{4}||Ainsi, les coordonnées du sommet sont |\displaystyle (h,k)=\left( -\frac{1}{4}, \frac{25}{8} \right).|
-
La variation : La fonction est croissante sur |]-\infty, -\frac{1}{4}]| et elle est décroissante sur |[-\frac{1}{4}, +\infty[.|
-
Les extrémums : étant donné que le graphique de la fonction est ouvert vers le bas, elle possède un maximum en |y=k,| c'est-à-dire que le maximum vaut ici |\frac{25}{8}.|
-
Les signes : la fonction est positive sur |[-1,5;\ 1]| et négative sur |]-\infty;\ -1,5] \cup [1, +\infty[.|
-
L'équation de l'axe de symétrie de la fonction est |x=h.| Donc ici, |x= -\dfrac{1}{4}.|
Pour déterminer les propriétés d'une fonction polynomiale du second degré, il est plus simple de travailler avec la forme canonique de la fonction.
Déterminez les propriétés de la fonction polynomiale du second degré d'équation ||f(x)=2(x-2)^2+5.||
Il peut être utile de tracer un graphique de la fonction.
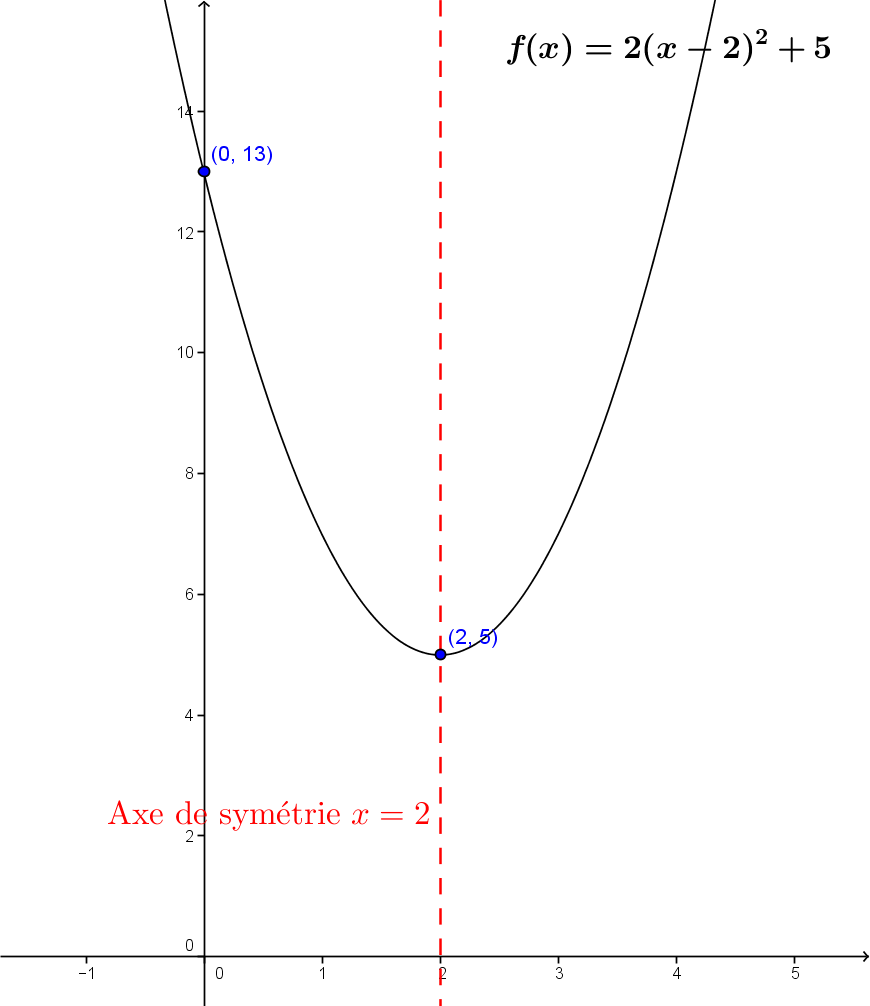
-
Le domaine de la fonction est |\mathbb{R}.|
-
L'image de la fonction est |[5, +\infty[.| En effet, le graphique de la fonction est ouvert vers le haut, car son paramètre |a| est positif et l'ordonnée du sommet est |5.|
-
L'ordonnée à l'origine d'une fonction quadratique sous la forme canonique se calcule en remplaçant |x| par |0.| ||\begin{align} f(x) &= 2(x-2)^2+5 \\ f(0) &= 2(0-2)^2+5 \\ f(0) &= 2(-2)^2+5 \\ f(0) &= 2 (4) + 5 \\ f(0) &= 8 + 5 \\ f(0) &= 13 \end{align}||L'ordonnée à l'origine de la fonction vaut donc |13.|
-
Comme l'ordonnée du sommet est plus grande que 0 et que le graphique de la fonction est ouvert vers le haut, cette dernière ne possède pas de zéro.
-
Les coordonnées du sommet sont |(h,k)=(2,5).|
-
La fonction est croissante sur |[2, +\infty[| et elle est décroissante sur |]-\infty,2].|
-
Étant donné que le graphique de la fonction est ouvert vers le haut, elle possède un minimum en |y=k|, c'est-à-dire que le minimum vaut |5.|
-
Comme l'image de la fonction est toujours positive |([5, + \infty[),| la fonction est positive sur tout son domaine.
-
L'équation de l'axe de symétrie de la fonction est |x=h.| Donc ici, |x=2.|
Pour valider ta compréhension des propriétés des fonctions de façon interactive, consulte la MiniRécup suivante :
