In the following animation, experiment with the parameters |a,| |b,| |h,| and |k| of the step function and observe the effects on the function. Afterwards, see the concept sheet to learn more about the function’s properties.
|
Property |
Characteristic of the Basic Form |
|---|---|
|
Equation |
|f(x)=[x]| |
|
Domain |
|\text{dom}f=\mathbb{R}| or depending on the context |
|
Range |
|\text{range}f=\mathbb{Z}| Only the integers |
|
|y|-intercept |
The graph of the basic step function crosses the |y|-axis at the origin, so the value of the |y|-intercept is |0|. |
|
|x|-intercept (zeroes of the function) |
The base function has zeroes over the following interval: |x \in [0,1[.| |
|
Variation: increasing and decreasing intervals |
The function is increasing over all |x|. It increases on |\mathbb{R}.| |
|
Vertex |
The graph does not have a vertex. |
|
Coordinates of a closed point of a step |
|(0,0)| |
|
Direction of points |
In the basic step function, each segment has a closed point on the left and an open point on the right. |
|
Extrema |
This function has no extrema. |
|
Positive and negative intervals |
The basic step function is positive for every |x \geq 0|. It is negative for every |x \leq 0|. |
|
Axis of symmetry |
The step function does not have an axis of symmetry |
|
Asymptotes |
There are no asymptotes. |
|
Property |
Characteristic of the Standard Form |
|---|---|
|
Equation |
|f(x)=a[b(x-h)]+k| |
|
Coordinates of a closed point of a step |
|(h,k)| |
|
Domain |
|\text{dom} f =\mathbb{R}| or depending on the context |
|
Range |
|\text{range} f= \lbrace an + k\ \text{where } n \in \mathbb{Z}\rbrace| |
|
Variation: increasing and decreasing intervals |
If the parameters |a| and |b| have the same sign |(a b>0),| the function is increasing. If the parameters |a| and |b| have opposite signs |(ab<0),| the function is decreasing. |
|
Zeroes of the function |
If they exist, they are the values of |x| where |f (x)=0|. For them to exist, it is necessary that |k| is a multiple of |a.| |
|
|y|-intercept |
The value of |f (0).| |
|
Direction of points |
If |b| is positive, each step has a closed point on the left and an open point on the right. If |b| is negative, each step has an open point on the left and a closed point on the right. |
|
Positive and negative intervals |
Positive interval: interval of |x| where |f(x)\geq 0.| Negative interval: interval of |x| where |f(x)\leq 0.| |
|
Extrema |
None, unless the domain is restricted by the context. |
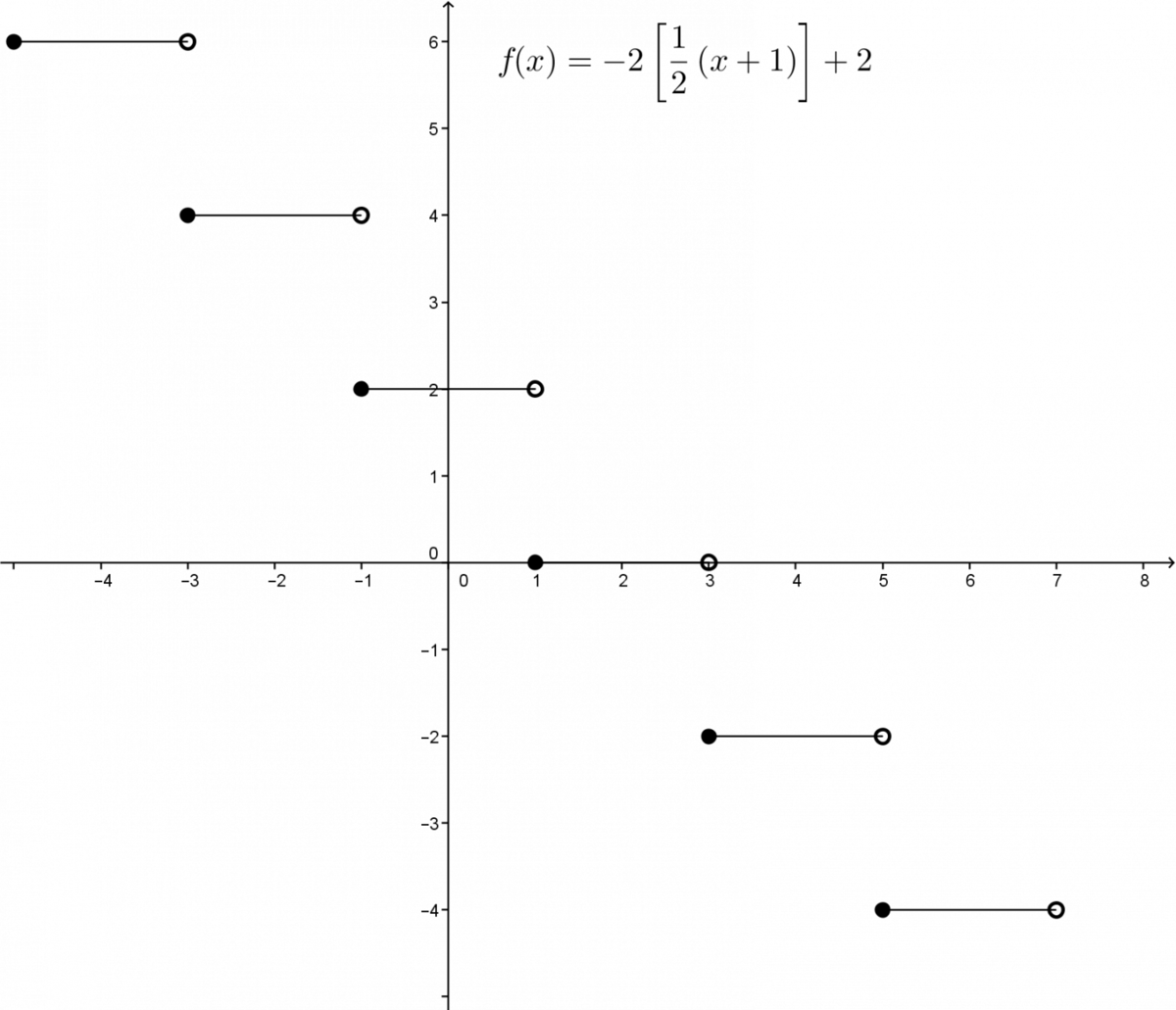
Determine the properties of the step function with the following equation. ||f(x)=-2\left[ \displaystyle \frac{1}{2}(x+1)\right]+2||
Drawing a graph of the function is recommended.
-
The coordinates of a closed end of a step are |(-1,2)=(h,k).|
-
The domain of the function is |\mathbb{R}.|
-
The range: since the parameter |k| has a value of |2| and the parameter |a| has a value of |-2,| the image of the function is: |\text{range } f= -2n + 2 \text{ where } n \in \mathbb{Z}|. The image of the function can also be expressed using curly brackets as |\lbrace ...,-4,-2,0,2,4,... \rbrace.|
-
The variation: the function is decreasing since the product |a \times b| is negative, given that |-2 \times \displaystyle \frac{1}{2} = -1.|
-
The function has zeroes since |2| is a multiple of |-2.| The zeroes can be determined either graphically or algebraically.
To calculate the zeroes, replace |f(x)| by |0| and then isolate the bracketed part. ||\begin{align}0 &= -2\left[ \displaystyle \frac{1}{2}(x+1) \right] + 2\\-2 &= -2\left[ \displaystyle \frac{1}{2}(x+1) \right]\\ 1 &= \left[ \displaystyle \frac{1}{2}(x+1) \right]\end{align}||Next, remember that if |[x]=a| for some |a \in \mathbb{Z},| then |a \leq x < a+1.|
Here, |a=1.| So, |1 \leq \displaystyle \frac{1}{2}(x+1) < 2|.
Now isolate |x|. ||\begin{align}1 &\leq \displaystyle \frac{1}{2}(x+1) < 2\\ 2 &\leq \phantom{\displaystyle \frac{1}{2}(}x+1\phantom{)}< 4\\1 &\leq \phantom{\displaystyle \frac{1}{2}(+} x \phantom{11)} < 3\end{align}||Therefore, the zeros of the function are the values of |x| in the interval |[1,3[.| -
The |y|-intercept of the function is calculated by replacing |x| with |0|. ||\begin{align}f(0) &= -2 \left[ \displaystyle \frac{1}{2}(0+1) \right] +2\\f(0) &= 2\end{align}|| Therefore, the |y|-intercept is |2.|
-
The direction of the points is full-empty (also defined as closed-open). This is because the parameter |b| is positive.
-
The positive and negative intervals:
-
The function is positive |(x \geq 0)| on the interval |]- \infty, 3[.|
-
It is strictly positive |(x>0)| on the interval |]-\infty, 1[.|
-
It is negative |(x \leq 0)| on the interval |[1, + \infty[.|
-
It is strictly negative |(x<0)| on the interval |[3,+\infty[.|
-
-
The function does not have any extrema.
