Dans l'animation suivante, tu peux modifier les paramètres |a,| |b,| |h| et |k| de la fonction partie entière et observer leurs effets sur les propriétés de la fonction. Après cette exploration, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions concernant les propriétés de la fonction.
| Propriétés | Caractéristiques de la forme de base |
|---|---|
| Règle | |f(x)=[x]| |
| Domaine | |\text{dom}f=\mathbb{R}| ou selon le contexte |
| Image (codomaine) |
|\text{ima}f=\mathbb{Z}|
Seulement les entiers
|
| Ordonnée à l'origine | Le graphique de la fonction partie entière de base coupe l'axe des |y| au point d'origine, alors la valeur de l'ordonnée à l'origine est |0|. |
|
Abscisse à l'origine
(zéros de la fonction)
|
Le graphique de la fonction de base possède des zéros sur l'intervalle suivant : |x \in [0,1[|. |
|
Croissance et
décroissance
|
La fonction est croissante pour tous les |x|.
Elle est croissante sur |\mathbb{R}|
|
| Sommet | Le graphique ne possède pas de sommet. |
| Coordonnées d'une extrémité fermée d'une marche | |(0,0)| |
| Sens des points | Dans la fonction de base, chaque segment a un point fermé à gauche et un point ouvert à droite. |
| Extrémums | Il n'y a aucun extrémum. |
| Signes |
La fonction partie entière de base est positive pour tous les |x \geq 0|.
Elle est négative pour tous les |x \leq 0|.
|
| Axe de symétrie | La fonction en escalier ne possède pas d'axe de symétrie |
| Asymptotes | Il n'y a pas d'asymptote. |
| Propriétés | Caractéristiques de la forme canonique |
|---|---|
| Règle | |f(x)=a[b(x-h)]+k| |
| Coordonnées d'une extrémité fermée d'une marche | |(h,k)| |
| Domaine | |\text{dom} f =\mathbb{R}| ou selon le contexte |
| Image (codomaine) | |\text{ima} f= \lbrace an + k \text{ où } n \in \mathbb{Z}\rbrace| |
| Croissance et décroissance |
Si les paramètres |a| et |b| sont de même signe |(a b>0),| la fonction est croissante.
Si les paramètres |a| et |b| sont de signes contraires |(ab<0),| la fonction est décroissante.
|
| Zéros de la fonction |
S'ils existent, ce sont les valeurs de |x| pour lesquelles |f (x)=0|.
Il faut que |k| soit un multiple de |a.|
|
| Ordonnée à l'origine | C'est la valeur de |f (0).| |
| Sens des points |
Si |b| est positif, chaque segment a un point fermé à gauche et un point ouvert à droite.
Si |b| est négatif, chaque segment a un point ouvert à gauche et un point fermé à droite.
|
| Signe de la fonction |
Fonction positive : intervalle de |x| sur lequel |f(x)\geq 0.|
Fonction négative : intervalle de |x| sur lequel |f(x)\leq 0.|
|
| Extrémums | Aucun, à moins que le domaine soit limité par le contexte. |
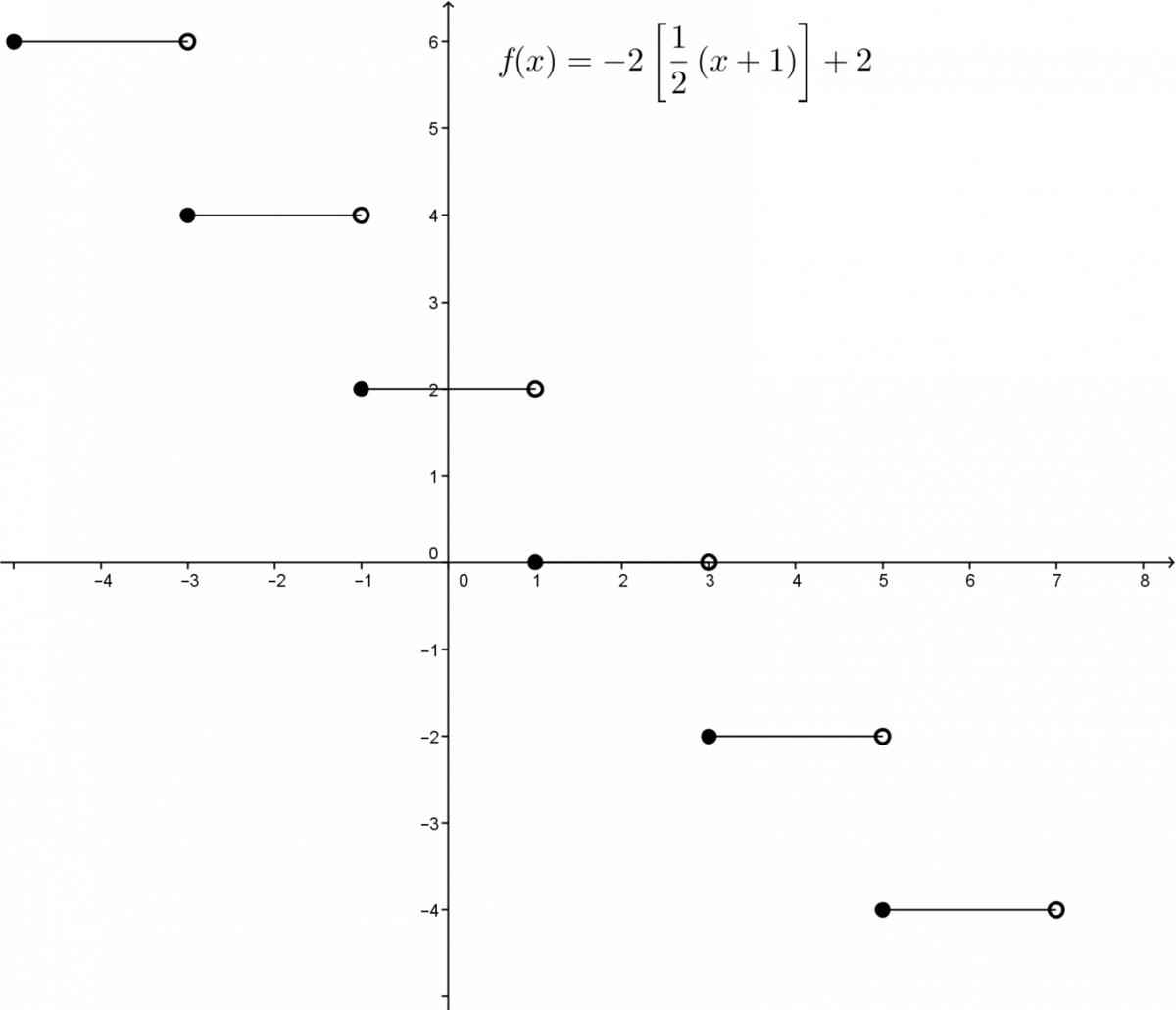
Déterminez les propriétés de la fonction en escalier d'équation : ||f(x)=-2\left[ \displaystyle \frac{1}{2}(x+1)\right]+2||
Il est suggéré de tracer un graphique de la fonction.
-
Les coordonnées de l'extrémité fermée d'une marche sont |(-1,2)=(h,k).|
-
Le domaine de la fonction est |\mathbb{R}.|
-
L'image : puisque le paramètre |k| vaut |2| et le paramètre |a,| |-2,| alors l'image de la fonction est donnée par |\text{ima } f= -2n + 2 \text{ où } n \in \mathbb{Z}|. On peut également donner l'image de la fonction avec des accolades |\lbrace ...,-4,-2,0,2,4,... \rbrace.|
-
La variation : la fonction est décroissante puisque le produit |a \times b| est négatif. En effet, |-2 \times \displaystyle \frac{1}{2} = -1.|
-
La fonction possède des zéros puisque |2| est un multiple de |-2.| On peut déterminer les zéros graphiquement ou encore algébriquement.
Pour y arriver, il faut remplacer |f(x)| par |0| puis ensuite isoler la partie entière : ||\begin{align}0 &= -2\left[ \displaystyle \frac{1}{2}(x+1) \right] + 2\\-2 &= -2\left[ \displaystyle \frac{1}{2}(x+1) \right]\\ 1 &= \left[ \displaystyle \frac{1}{2}(x+1) \right]\end{align}||Rendu ici, il faut se souvenir que si |[x]=a| avec |a \in \mathbb{Z},| alors |a \leq x < a+1.|
Ici, |a=1.| Ainsi, |1 \leq \displaystyle \frac{1}{2}(x+1) < 2|.
Il faut maintenant isoler |x|. ||\begin{align}1 &\leq \displaystyle \frac{1}{2}(x+1) < 2\\ 2 &\leq \phantom{\displaystyle \frac{1}{2}(}x+1\phantom{)}< 4\\1 &\leq \phantom{\displaystyle \frac{1}{2}(+} x \phantom{11)} < 3\end{align}||Par conséquent, les zéros de la fonctions sont les |x| dans l'intervalle |[1,3[.| -
L'ordonnée à l'origine de la fonction se calcule en remplaçant |x| par |0|. ||\begin{align}f(0) &= -2 \left[ \displaystyle \frac{1}{2}(0+1) \right] +2\\f(0) &= 2\end{align}|| L'ordonnée à l'origine est donc |2.|
-
Le sens des points est plein-vide (on peut également dire fermé-ouvert). En effet, le paramètre |b| est positif.
-
Les signes :
-
La fonction est positive |(x \geq 0)| sur l'intervalle |]- \infty, 3[.|
-
Elle est strictement positive |(x>0)| sur l'intervalle |]-\infty, 1[.|
-
Elle est négative |(x \leq 0)| sur l'intervalle |[1, + \infty[.|
-
Elle est strictement négative |(x<0)| sur l'intervalle |[3,+\infty[.|
-
-
La fonction n'admet aucun extrémum.
Pour valider ta compréhension des propriétés des fonctions de façon interactive, consulte la MiniRécup suivante :
