-
An event is a subset of a random experiment's sample space.
-
The elements that belong to this type of subset are called the outcomes (or results) that are favourable to the event happening.
In a random experiment, we can predict a future event that has a chance of happening, but is still unknown.
We may be interested in several events when rolling a |6|-sided die numbered from |1| to |6.| In such a case, the sample space of all possible outcomes is |\Omega=\{1,2,3,4,5,6\}.|
|
Example of an event |
Favourable outcomes of the event |
|---|---|
|
|A:| Rolling a |3.| |
|A=\{3\}| |
|
|B:| Rolling an odd number. |
|B=\{1,3,5\}| |
|
|C:| Rolling a number greater than |4.| |
|C=\{5,6\}| |
|
|D:| Rolling a prime number |
|D=\{2,3,5\}| |
Note: An event is always represented with a capital letter.
An event can correspond to a single outcome, to several outcomes or to all the outcomes in the sample space. It can also correspond to no result or outcome. Therefore, we distinguish between different types of events.
A simple event is an event that contains only one outcome of the sample space.
-
We choose a card from a |52|-card deck at random. The event "to draw the 2 of spades" is a simple event, because it contains only one outcome of the sample space. The probability of this event occurring is |\dfrac{1}{52}.|
-
The event "to roll a 3" when rolling a |6|-sided die is a simple event, because it has only one outcome in the sample space. The probability of this event occurring is |\dfrac{1}{6}.|
The sum of the probabilities of all the simple events of a random experiment is equal to |1,| or |100\ \%.|
-
A certain event is an event that always occurs. It corresponds to the entire sample space and its probability is |100\ \%.|
-
A probable (possible) event is an event that may happen. It corresponds to a non-empty subset of the sample space and its probability is between |0\ \%| and |100\ \%.|
-
An impossible event is an event that cannot occur. Its outcomes do not correspond to any of the outcomes of the sample space and its probability is |0\ \%.|
Certain, probable and impossible events can be illustrated on a probability line. On this line, the further to the left an outcome is located, the less likely it is to occur.

Here are some examples for events associated with the experiment "rolling a 6-sided die."

-
The event “drawing a red marble" when randomly picking a marble from a bag containing |3| red marbles is a certain event, because the event corresponds to the entire sample space of possible outcomes. The probability of this event happening is |\dfrac{3}{3},| |1| or |100\ \%.|
-
The event "getting tails" when tossing a coin is a probable event, because it corresponds to a non-empty subset of the sample space. The probability of this event happening is |\dfrac{1}{2},| or |50\ \%.|
-
The event "drawing a green marble" when a marble is randomly picked from a bag that contains |2| red and |3| blue marbles is an impossible event, because there are no green marbles in the bag. The probability of this event is |0.|
Equiprobable events are events that have the same chance of occurring.
-
Event |A| "getting a number less than 2" and Event |B| "getting a number greater than 5" when a 6-sided die is rolled are 2 equiprobable events, since they have the same chance of occuring. The probability of event |A| is |P(A)=\dfrac{1}{6}| and the probability of event |B| is |P(B)=\dfrac{1}{6},| since they each have only one favourable outcome.
-
Event |C| "drawing a king" and Event |D| "drawing a 5" when a card is randomly picked from a |52|-card deck are equiprobable events, since they have the same chance of occurring. The probability of Event |C| is |P(C)=\dfrac{1}{13}| and the probability of Event |D| is |P(D)=\dfrac{1}{13},| since they each have |4| favourable outcomes out of a total of |52.|
It is possible to compare the probabilities of several events.
-
An event is less likely when it has less chance of happening than another event.
-
An event is more likely when it has more chance of happening than another event.
Event |A| “drawing a diamond" in a 52-card deck is more probable than event |B| "drawing a queen," since it has more chances to occur. Indeed, the probability of Event |A| happening is |P(A)=\dfrac{13}{52}|, while the probability of Event |B| happening is |P(B)=\dfrac{4}{52}.|
We can also say that Event |B| is less likely than Event |A,| since its probability is lower.
-
Compatible events are events that have at least one favourable outcome in common.
-
Incompatible events are events that have no favourable outcomes in common.
For 2 events |A| and |B| to be compatible, their intersection must not be empty |(A \cap B \neq \varnothing).| Therefore, there is at least one favourable outcome common to both events.
Conversely, the intersection between incompatible events is empty |(A \cap B = \varnothing).|
We are interested in the following 3 events when rolling a 6-sided die.
-
Event |A| "rolling an even number"
-
Event |B| "rolling a 2, a 3, or a 5 "
-
Event |C| "rolling a 1"
Event |A| and Event |B| are compatible events since |2| is a favourable outcome that is common to both events |(A \cap B = \{2\}).|
By representing the sample space in a Venn diagram, we see that there is a value in the intersection of |A| and |B.|
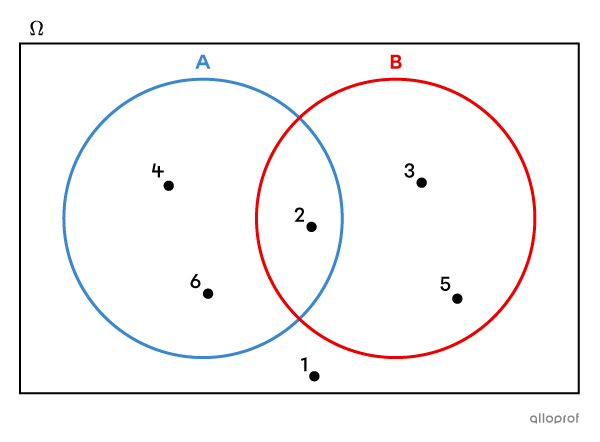
Event |A| and event |C| are incompatible events since they have no favourable outcomes in common.
By representing the sample space in a Venn diagram, we can see that there are no values in the intersection of |A| and |C.|
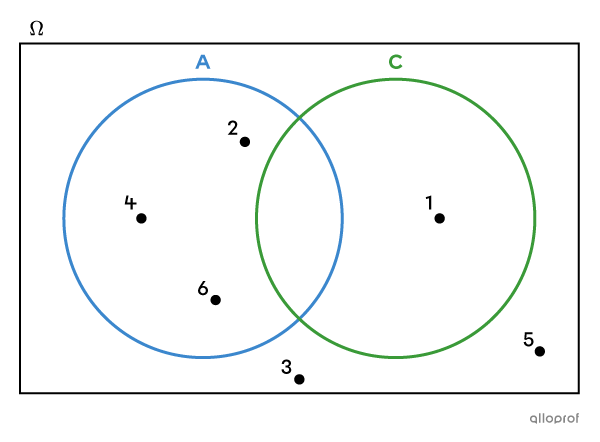
When 2 events are compatible, the probability that Event |A| or Event |B| occurs is |P(A \cup B) = P(A) + P(B) - P(A \cap B).|
We can use the same formula for incompatible events, but since |P(A\cap B)=0,| the formula simply becomes |P(A \cup B) = P(A) + P(B).|
Complementary events are incompatible events whose union corresponds to the entire sample space.
For 2 events |A| and |B| to be complementary, their intersection must be empty |(A \cap B = \varnothing)| and the union of their favourable outcomes must be equal to the entire sample space |(A \cup B = \Omega).|
The sum of the probabilities of 2 complementary events |A| and |B| is |1,| or |100\ \%.|
||P(A) + P(B) = 1||
Note: In general, the complementary event to Event |A| is denoted |A'| or |A^c.|
- Event |A| "getting a red card" and Event |B| "getting a black card" are complementary events, since the union of their favourable outcomes corresponds to the whole set of cards contained in a 52-card deck. The sum of the probabilities of these events is equal to |1.|
||P(A) + P(B) = \dfrac{26}{52} + \dfrac{26}{52} =\dfrac{52}{52}= 1||
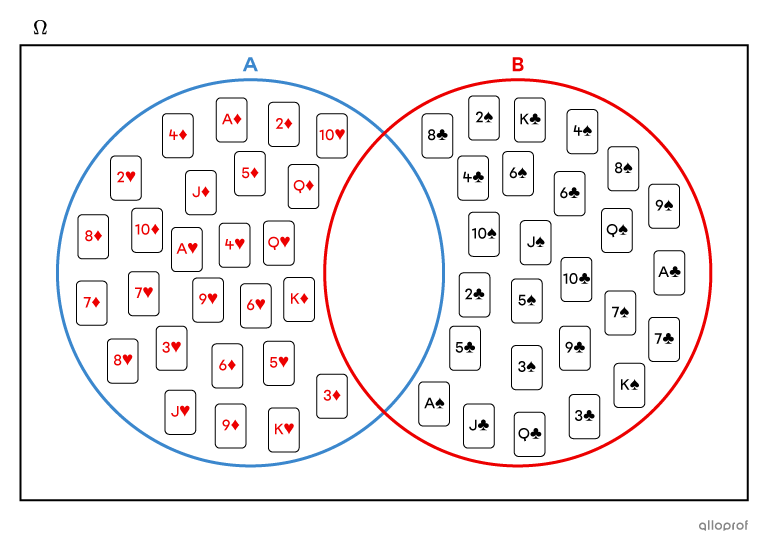
- Events |A| "rolling an even number" and |B| "rolling an odd number" when we toss a 6-sided die are complementary events, since the union of their favourable outcomes corresponds to the whole sample space and there is no element in their intersection.
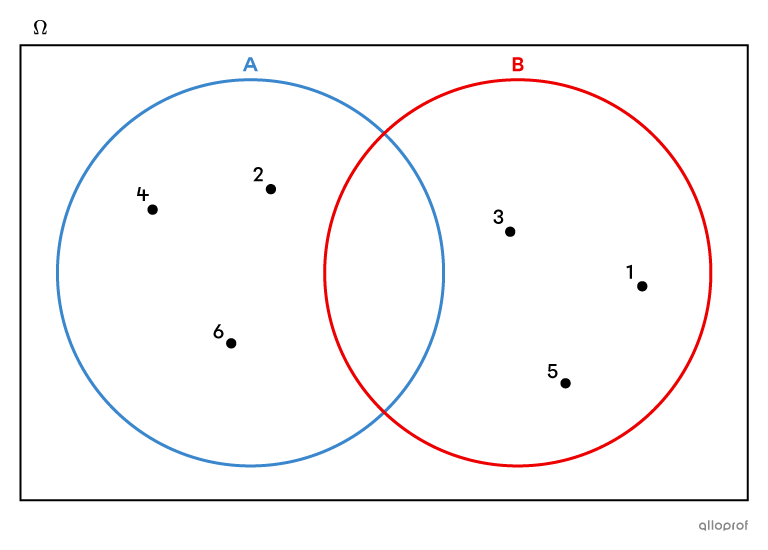
When we are looking for the probability of an event |A| and we know the probability of its complementary event |A',| we can use the relationship |P(A)+P(A')=1| and isolate |P(A).|
It is estimated that |75\ \%| of Secondary 2 students do not wear glasses. Knowing this, what is the probability that a randomly selected high school student wears glasses?
The events "wearing glasses" and "not wearing glasses" are complementary events. Their intersection is empty, since a student cannot wear glasses and not wear them simultaneously. Also, since "wearing glasses" and "not wearing glasses" are the only 2 possible options, the union of these sets contains all the elements of the sample space. Therefore, we have |P(A)+P(A')=1.|
||\begin{align}P(\text{glasses}) + P(\text{no glasses})&=1\\P(\text{glasses})&=1-P(\text{no glasses})\\&=1-0.75\\&=0.25\end{align}||
Answer: The probability that a randomly chosen Secondary 2 student wears glasses is |25\ \%.|
Note: Having a certain characteristic and not having that same characteristic are always complementary events.
-
Dependent events are events where the occurrence of one affects the occurrence of the other.
-
Independent events are events where the occurrence of one does not affect the occurrence of the other.
In a multi-step random experiment with replacement, the events are often independent. In experiments without replacement, the events are dependent.
-
When a die is rolled |2| times, the probability of getting a |3| on the 2nd toss is not affected by the probability of getting a |5| on the 1st, since the |2| rolls are independent events.
On the other hand, when we roll a die |2| times, the probability of rolling a sum of |10| is influenced by the result of the 1st roll. If we get a |1| on the first roll, it is impossible to get a sum of |10,| whereas if we get a |5| on the first roll, it is still possible to get a sum of |10.| -
We randomly draw |2| cards from a deck of |52| cards. As there is no replacement, the 2nd event is influenced by the 1st, since there are only |51| cards left in the deck after the 1st event. The probability of the 2nd event is therefore dependent on the 1st event.
The probability of two independent events |A| and |B| simultaneously occurring is expressed as |P(A \cap B) = P(A) \times P(B).| This property is called the multiplication rule.
However, in a multi-step random experiment, if events |A| and |B| are dependent, this is expressed as |P(A \cap B) \neq P(A) \times P(B).|
-
Mutually exclusive events are events that have no favourable outcomes in common |(A \cap B = \varnothing).|
-
Non-mutually exclusive events are events that have at least one favourable outcome in common |(A \cap B \neq \varnothing).|
When 2 events are non-mutually exclusive, the probability of event |A| or event |B| occurring is |P(A \cup B) = P(A) + P(B) - P(A \cap B).|
We can use the same formula for mutually exclusive events, but since |P(A\cap B)=0,| the formula simply becomes |P(A \cup B) = P(A) + P(B).|
-
A card is randomly drawn from a |52| card deck. Event |A| "getting a heart" and Event |B| "getting a black card" are mutually exclusive events because they have nothing in common. A card cannot be a heart and black at the same time.
-
A card is randomly drawn from a |52| card deck. Event |A| "getting a king" and Event |B| "getting a black card" are non-mutually exclusive events because they have favourable outcomes in common: the kings of spades and clubs are both kings and both are black cards.
Two |6|-sided dice are rolled and the sum of the results is calculated.
-
Event |A,| "getting a sum of 2," is a simple event, because it contains only one outcome of the sample space: |A=\{(1,1)\}.|
-
Event |B,| "getting a sum less than 15," is a certain event, because it contains all the outcomes of the sample set since it always happens. This is because the sum of |2| dice with |6| sides is always between |2| and |12| inclusively.
-
Event |C,| "getting a sum of 15," is an impossible event, because it does not contain any outcome from the sample space. In fact, the largest possible sum of |2| dice with |6| faces is |12|.
-
Events |D|, "getting a sum of 12," and |A|, "getting a sum of 2," are equiprobable, because both events have the same probability of occurring. More specifically, the |2| events have only one favourable outcome. |A=\{(1,1)\}| and |D=\{(6,6)\}.|
-
Event |E|, "getting a sum of 4," is more likely than Event |A|, "getting a sum of 2." This is because there are |3| favourable outcomes for Event |D,| which are |{(1,3), (2,2), (3,1)},| whereas Event |A| has only one favourable outcome.
-
Events |F|, "getting at least one 2," and |A|, "getting a sum of 2," are incompatible because they have no favourable outcomes in common.
-
Events |G|, "getting a sum greater than 2," and |A|, "getting a sum of 2," are complementary, because they are incompatible and the union of their results corresponds to the entire sample space.
-
Events |H|, "getting a sum of 8," and |F|, "getting at least one 2," are dependent, because the occurrence of one affects the occurrence of the other.