A multi-step random experiment can be performed with or without replacing the possible options at each step.
|2| marbles are drawn from a bag that contains |3| blue marbles and |1| red marble.
The probability that a red marble is drawn first is |\dfrac{1}{4},| because there is |1| red marble out of a total of |4| marbles.
The marble is replaced in the bag
The probability that the 2nd marble drawn is red is |\boldsymbol{\dfrac{1}{4}}.| There is still |1| red marble in the bag containing a total of |4| marbles.
The marble is not replaced in the bag
The probability that the 2nd marble drawn is red is |\boldsymbol{\dfrac{0}{3}}.| There are no more red marbles in the bag, which now contains a total of |3| marbles.
It is not always clear if a random experiment is with or without replacement. Sometimes the context has to be analyzed to know for sure. Here are some examples.
With replacement
-
Flipping a coin
-
Rolling a die
Without replacement
-
Lottery
-
Bingo
Some random experiments can be with or without replacement, depending on the context. Here are some examples.
-
Drawing |1| card from a 52-card deck. The card may or may not be replaced in the deck after being drawn.
-
Drawing |1| marble from a bag. The marble may or may not be replaced in the bag after being drawn.
When analyzing a multi-step random experiment with or without replacement, it is also important to check if the order matters or not.
A multi-step random experiment with replacement is an experiment where the possible outcomes of the previous step are the same in the next step.
In a multi-step random experiment with replacement, the probabilities do not change from one step to the next. The events are said to be independent.
|1| marble is drawn from a bag containing |7| marbles of different colours. The marble is then replaced in the bag, and a 2nd marble is drawn.
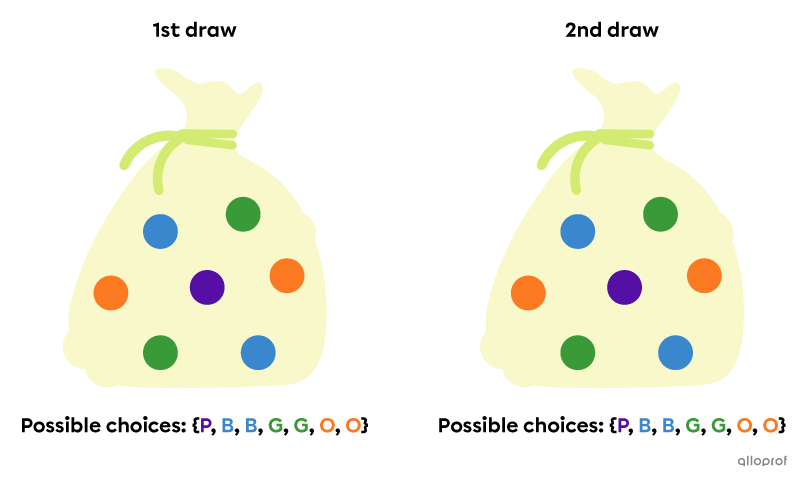
Since the 1st marble is returned to the bag after being drawn, the possible outcomes are the same for the 2nd draw.
The probability of drawing a marble of a certain colour stays the same at each step. The result of each draw is independent of the previous one.
To find the probability of an event in a multi-step random experiment with replacement, the multiplication rule can be used.
Julie enters a game of chance to win a bicycle. In the game, Julie must draw a coloured card from an opaque jar that contains |3| green and |5| red cards. She must then replace the card in the jar and draw a second card. To win the game, Julie must draw |2| green cards.
What is the probability that Julie wins the bicycle?
This random experiment is carried out with replacement, since Julie has to draw a card, put it back in the jar, and then draw a second one. Therefore, the total number of cards does not change from one step to the next
We start by calculating the probability of each possible choice on the 1st step.
||\begin{align}P(\text{Green})&=\dfrac{\text{Number of Green Cards}}{\text{Total Number of cards}}\\&=\dfrac{3}{8}\\\\P(\text{Red})&=\dfrac{\text{Number of Red Cards}}{\text{Total Number of cards}}\\&=\dfrac{5}{8}\end{align}||
Since the experiment is with replacement, the probabilities for the second step stay the same.
Next, the probability of each possible outcome is calculated by multiplying the probability at the 1st step and the probability at the 2nd step.
||\begin{align}P(\text{Green,Green})&=\dfrac{3}{8}\times\dfrac{3}{8}=\dfrac{9}{64}\\P(\text{Green, Red})&=\dfrac{3}{8}\times\dfrac{5}{8}=\dfrac{15}{64}\\P(\text{Red, Green})&=\dfrac{5}{8}\times\dfrac{3}{8}=\dfrac{15}{64}\\P(\text{Red, Red})&=\dfrac{5}{8}\times\dfrac{5}{8}=\dfrac{25}{64}\end{align}||
To help answer the question, a tree diagram can be constructed.
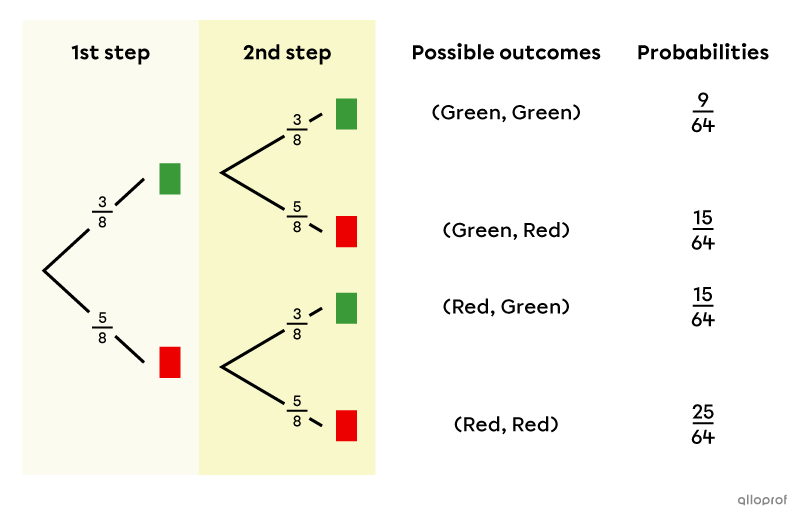
Answer: The probability that Julie wins the bicycle is |\dfrac{9}{64},| or about |14\ \%.|
A multi-step random experiment without replacement is an experiment where there are more possible outcomes in the previous step than in the next step.
In a multi-step random experiment without replacement, the probabilities change from one step to the next. The events are said to be dependent.
|1| marble is drawn from a bag containing |7| different coloured marbles. A second marble is drawn, without placing the first marble back into the bag.
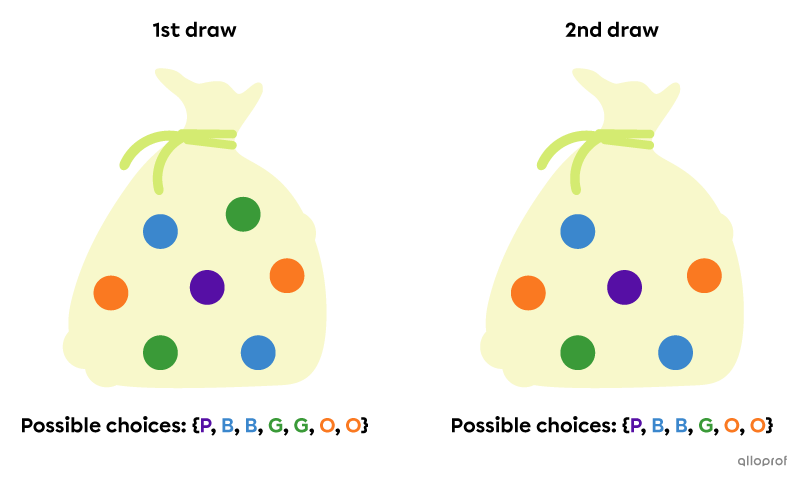
Since the first marble is not replaced in the bag after being drawn, the possible outcomes are different for the 2nd step.
The probability of drawing a marble of a certain colour is therefore also different at each step. Also, the outcome of each step is dependent on the one that came before.
To find the probability of an event in a multi-step random experiment without replacement, the multiplication rule can be used.
Julie enters a game of chance to win a bicycle. In the game, Julie must draw |2| coloured cards from an opaque jar containing |3| green and |5| red cards. To win the game, Julie must draw |2| green cards.
What is the probability that Julie wins the bicycle?
This random experiment is carried out without replacement, since there is no indication that Julie must return the first drawn card to the jar. Therefore, the total number of cards changes from one step to the next.
We start by calculating the probability of each possible choice for the 1st step.
||\begin{align}P(\text{Green})&=\dfrac{\text{Number of Green Cards}}{\text{Total Number of Cards}}\\&=\dfrac{3}{8}\\\\P(\text{Red})&=\dfrac{\text{Number of Red Cards}}{\text{Total Number of Cards}}\\&=\dfrac{5}{8}\end{align}||
Since the experiment is carried out without replacement, the probabilities change at the 2nd step. This is because there is |1| less card in the jar, which means that the denominator of the fractions changes from |8| to |7| and the numerator decreases by |1,| depending on the outcome of the first step.
Next, the probability of each possible outcome is calculated by multiplying the probability at the 1st step with the probability at the 2nd step.
||\begin{align}P(\text{Green, Green})&=\dfrac{3}{8}\times\dfrac{2}{7}=\dfrac{6}{56}\\P(\text{Green, Red})&=\dfrac{3}{8}\times\dfrac{5}{7}=\dfrac{15}{56}\\P(\text{Red, Green})&=\dfrac{5}{8}\times\dfrac{3}{7}=\dfrac{15}{56}\\P(\text{Red, Red})&=\dfrac{5}{8}\times\dfrac{4}{7}=\dfrac{20}{56}\end{align}||
To help answer the question, a tree diagram can be constructed.
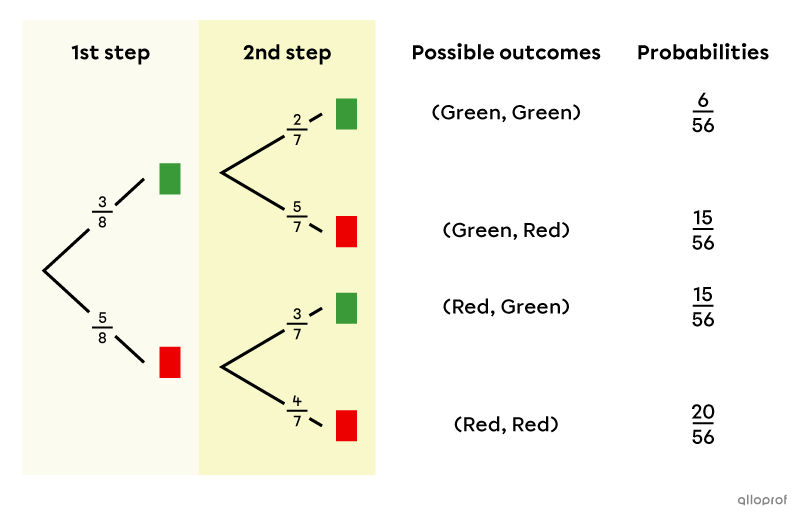
Answer: The probability that Julie wins the bicycle is |\dfrac{6}{56},| or about |11\ \%.|
Here is an example of a random experiment without replacement where the order doesn't matter.
On his birthday, Forrest is given a box of |10| chocolates by his mother. She knows that Forrest would eat all the chocolates at once, so his mother suggests that he close his eyes and eat |3| at random. In the box, there are |4| dark chocolates |(D),| |4| milk chocolates |(M)| and |2| white chocolates |(W).|
What is the probability that Forrest will eat one chocolate of each kind?
This random experiment is carried out without replacement, since Forrest does not return the chocolates to the box after eating them. Therefore, the total number of chocolates changes from one step to the next. As well, the order of the chocolates does not matter, since we are only interested in the type of chocolates Forrest eats.
We start by calculating the probability of each possible choice of the 1st step.
||\begin{align}P(N)&=\dfrac{\text{Number of Dark Chocolates}}{\text{Total Number of Chocolates}}\\&=\dfrac{4}{10}\\\\P(L)&=\dfrac{\text{Number of Milk Chocolates}}{\text{Total Number of Chocolates}}\\&=\dfrac{4}{10}\\\\P(B)&=\dfrac{\text{Number of White Chocolates}}{\text{Total Number of Chocolates}}\\&=\dfrac{2}{10}\end{align}||
Since this experiment is carried out without replacement, the probabilities change at the 2nd step. This is because there is |1| less chocolate in the box, which implies that the denominator of the fractions changes from |10| to |9.| As well, the numerator decreases by |1| depending on the result obtained in the first step. The same is true for step 3.
To help answer the question, a tree diagram can be constructed.
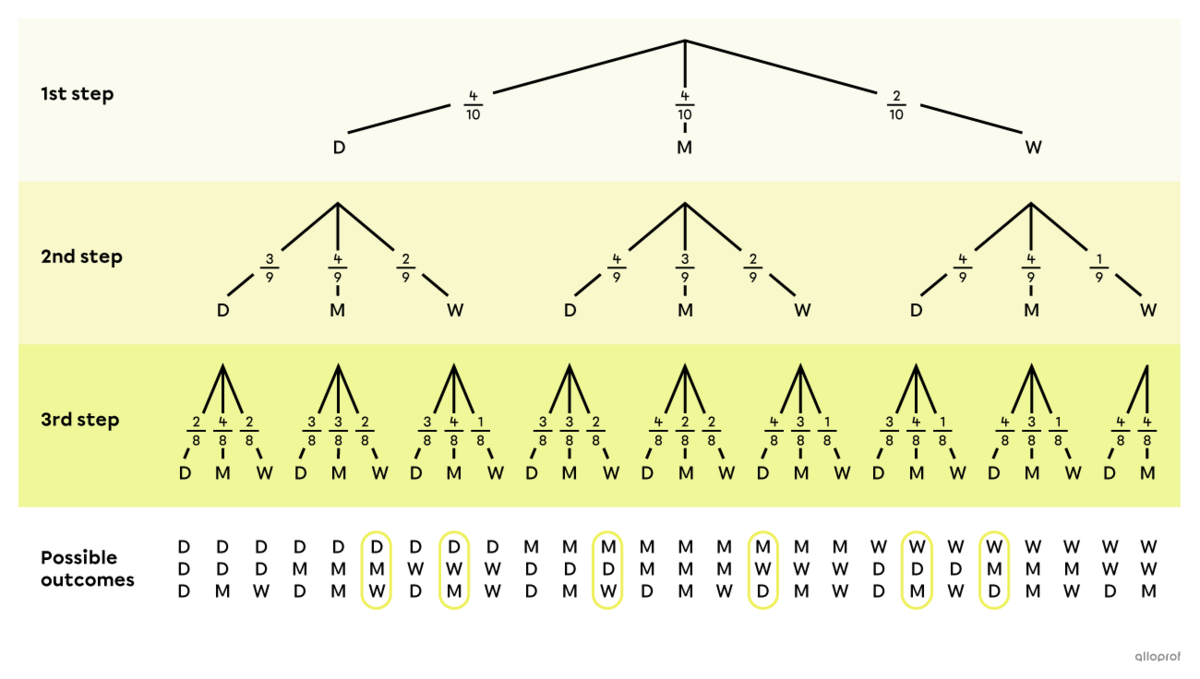
Next, the possible outcomes that correspond to the event "eat one of each type of chocolate" are identified in the tree diagram. These possible outcomes are as follows:
||\begin{aligned}&(D,M,W)&&(D,W,M)\\&(M,D,W)&&(M,W,D)\\&(W,D,M)&&(W,M,D)\end{aligned}||
The probabilities of each of these outcomes are calculated first using the multiplication rule.
||\begin{align}P(D,M,W)&=\dfrac{4}{10}\times\dfrac{4}{9}\times\dfrac{2}{8}=\dfrac{32}{720}\\P(D,W,M)&=\dfrac{4}{10}\times\dfrac{2}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\P(M,D,W)&=\dfrac{4}{10}\times\dfrac{4}{9}\times\dfrac{2}{8}=\dfrac{32}{720}\\P(M,W,D)&=\dfrac{4}{10}\times\dfrac{2}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\P(W,D,M)&=\dfrac{2}{10}\times\dfrac{4}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\P(W,M,D)&=\dfrac{2}{10}\times\dfrac{4}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\\end{align}||
All the fractions are added together.
||\begin{align}P\left(\begin{gathered}\text{Eating one chocolate}\\\text{of each kind}\end{gathered}\right)&=\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}\\&=6\times\dfrac{32}{720}\\&=\dfrac{192}{720}\end{align}||
Finally, reduce the fraction.
||\begin{align}P\left(\begin{gathered}\text{Eating one chocolate}\\\text{of each kind}\end{gathered}\right)&=\dfrac{192\boldsymbol{\color{#ec0000}{\div48}}}{720\boldsymbol{\color{#ec0000}{\div48}}}\\&=\dfrac{4}{15}\end{align}||
Answer: The probability that Forrest eats one chocolate of each kind is |\dfrac{4}{15},| or |26.\overline{6}\ \%.|