A reflection (or symmetry) is a transformation that generates an inverted image with respect to an axis of reflection.
The axis of reflection is located halfway between the initial figure and the image figure.
On a Cartesian plane, certain axes can be defined as axes of reflection, making it possible to define the reflection using simple rules.
These axes are:
-
the |x|-axis
-
the |y|-axis
-
the quadrant bisectors (lines that separate the quadrants into two equal parts).
A figure can be reflected with respect to the |x|-axis, the |y|-axis, or the quadrant bisectors.
There is a rule associated with each axis of reflection.
The |x|-axis: |s_x: (x, y) \mapsto (x, -y)|
The |y|-axis: |s_y: (x, y) \mapsto (-x, y)|
The 1st bisector of quadrants 1 and 3: |s_/: (x, y)\mapsto (y, x)|
The 2nd bisector of quadrants 2 and 4: |s_{\backslash}: (x, y) \mapsto (-y, -x)|
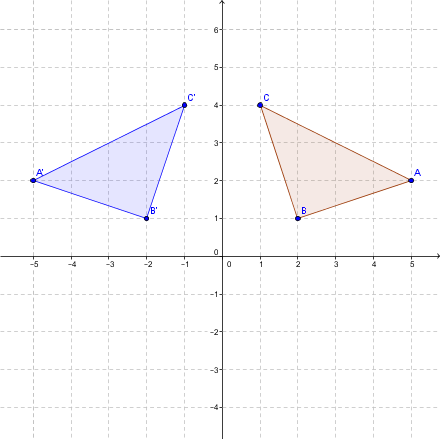
Example of a reflection with respect to the |y|-axis
Reflect triangle |ABC| across the |y|-axis.

Step 1: Identify the vertices of triangle |ABC.|
|A (5, 2)|
|B (2, 1)|
|C (1, 4)|
Step 2: Perform the reflection using the following rule:
|s_y:(x,y) \mapsto (-x,y).|
The vertices of the triangle become:
|A =(5, 2) \mapsto (-5, 2) = A’|
|B =(2, 1) \mapsto (-2, 1) = B’|
|C =(1, 4) \mapsto (-1, 4) = C’|
Step 3: Graph the final blue triangle.
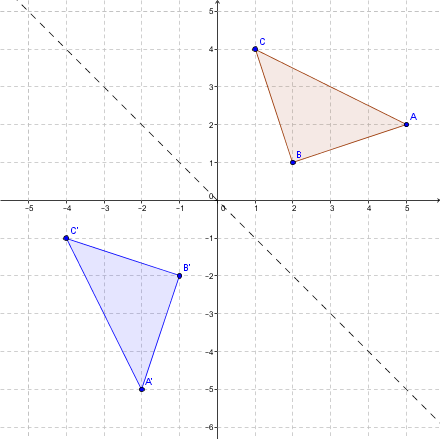
Example of a reflection with respect to the 2nd bisector of quadrants 2 and 4
Reflect triangle |ABC| across the 2nd bisector.
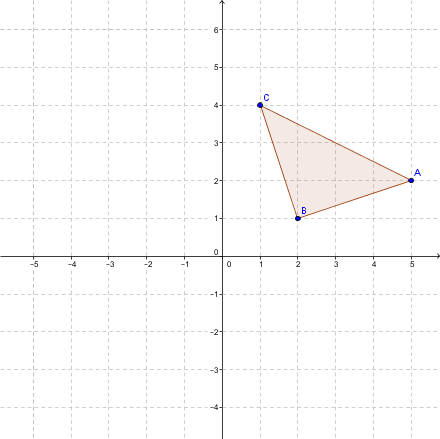
Step 1: Identify the vertices of triangle |ABC.|
|A (5, 2)|
|B (2, 1)|
|C (1, 4)|
Step 2: Perform the reflection using the following rule:
|s_{\backslash}:(x,y) \mapsto (-y,-x).|
The vertices of the triangle become:
|A=(5, 2) \mapsto (-2, -5)=A'|
|B=(2, 1) \mapsto (-1, -2)=B'|
|C=(1, 4) \mapsto (-4, -1)=C'|
Step 3: Graph the final blue triangle.