La réflexion (ou symétrie) est une transformation qui génère une image renversée par rapport à un axe de réflexion.
L’axe de réflexion se trouve à mi-chemin entre la figure initiale et la figure image.
Dans un plan cartésien, certains axes définis comme axes de réflexion permettent de décrire la réflexion sous la forme de règles simples.
Ces axes sont :
- l'axe des abscisses;
- l'axe des ordonnées;
- les bissectrices (lignes qui séparent un angle en deux parties égales) des quadrants.
Ainsi, on peut effectuer la réflexion d’une figure par rapport à l’axe des abscisses ou des ordonnées, ou par rapport aux bissectrices des quadrants.
Une règle est associée à chaque axe de réflexion.
L’axe des abscisses: |s_x : (x , y) \mapsto (x , -y)|;
L’axe des ordonnées: |s_y: (x , y) \mapsto (-x , y)|;
La bissectrice des quadrants 1 et 3: |s_/: (x , y)\mapsto (y , x)|;
La bissectrice des quadrants 2 et 4: |s_{\backslash}: (x , y) \mapsto (-y , -x)|.
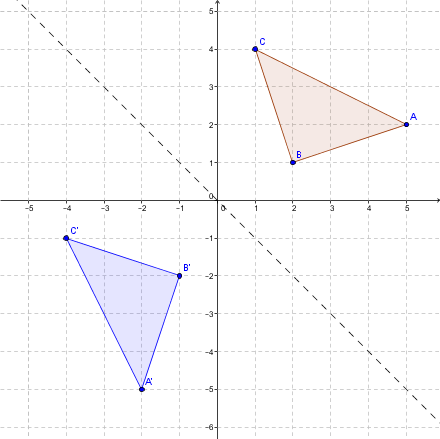
Exemple de réflexion par rapport à l'axe des |y| (ordonnées)
Effectue la réflexion indiquée du triangle |ABC|.
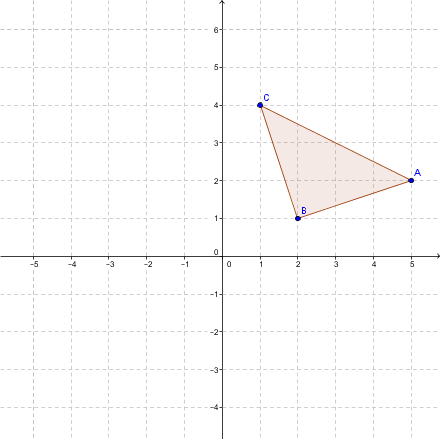
Étape 1 : On identifie les sommets du triangle |ABC|.
|A (5, 2)|
|B (2, 1)|
|C (1, 4)|
Étape 2 : On effectue la réflexion à l’aide de la règle suivante:
|s_y:(x,y) \mapsto (-x,y)|.
Les sommets du triangle deviennent donc:
|A =(5 , 2) \mapsto (-5 , 2) = A’|;
|B =(2 , 1) \mapsto (-2 , 1) = B’|;
|C =(1 , 4) \mapsto (-1 , 4) = C’|.
Étape 3 : On trace le triangle final bleu.
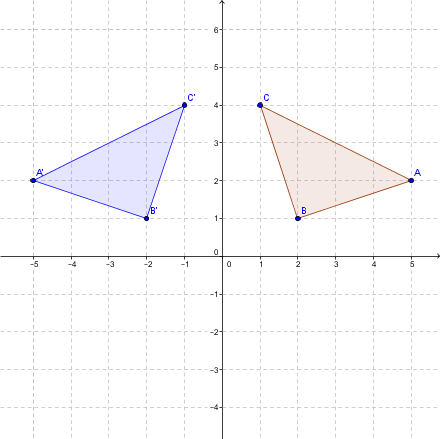
Exemple de réflexion par rapport à la bissectrice des quadrants 2 et 4
Effectue la réflexion indiquée du triangle |ABC|.
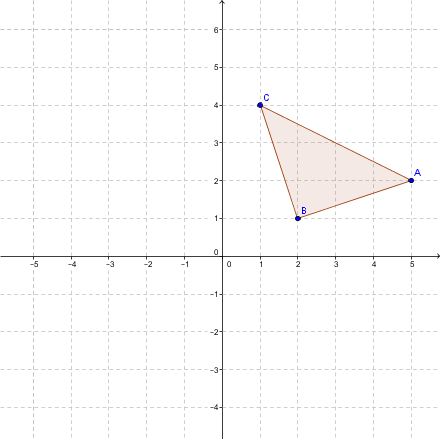
Étape 1 : On identifie les sommets du triangle |ABC|.
|A (5, 2)|
|B (2, 1)|
|C (1, 4)|
Étape 2 : On effectue la réflexion à l’aide de la règle suivante:
|s_{\backslash}:(x,y) \mapsto (-y,-x)|.
Les sommets du triangle deviennent donc:
|A=(5 , 2) \mapsto (-2 , -5)=A'|;
|B=(2 , 1) \mapsto (-1 , -2)=B'|;
|C=(1 , 4) \mapsto (-4 , -1)=C'|.
Étape 3 : On trace le triangle final bleu.