Pour la majorité des fonctions, il existe plusieurs équations qui permettent d'exprimer la même courbe. Il est très pratique d'utiliser une forme qui donne le plus d'informations possible. La forme canonique en est une.
La forme canonique est une forme d'écriture paramétrique de l'équation d'une fonction. On dit que la forme canonique d'une fonction est porteuse de sens puisqu'elle donne de l'information sur l'allure de son graphique. On l'appelle aussi forme transformée.
Dans l'équation d'une fonction écrite sous forme canonique, il y a des paramètres.
Un paramètre est une grandeur dont la valeur numérique doit être fixée dans une expression algébrique ou une équation. On désigne généralement les différents paramètres par des lettres (différentes des variables).
La modification des paramètres permet d'obtenir une courbe ayant un aspect différent de celui de la forme de base. La courbe peut subir une translation, un allongement, un rétrécissement ou une réflexion.
On distingue généralement 4 paramètres appelés |a|, |b|, |h| et |k|. Ces paramètres jouent tous des rôles particuliers. On peut regrouper les 4 paramètres en 2 catégories : les paramètres additifs et les paramètres multiplicatifs.
La règle d'une fonction de base |y=f(x)| à laquelle on ajoute des paramètres devient sous la forme canonique :
||y=af\big(b(x-h)\big)+k||où |f| est la fonction
La formule précédente illustre où les différents paramètres se situent lorsqu'on les ajoute à la forme de base.
Voici un tableau qui présente les formes de base, les formes canoniques et les formes canoniques réduites de différentes fonctions.
| Formes de base | Formes canoniques | Formes canoniques réduites |
|---|---|---|
| |y=x| | |y=ax+k| On remplace généralement le |k| par un |b|. Il ne faut pas confondre le rôle de |k| avec le rôle de |b.| |
|
| |y=x^2| | |y=a\big(b(x-h)\big)^2+k| | |y=a(x-h)^2+k| |
| |y=\dfrac{1}{x}| | |y=\dfrac{a}{b(x-h)}+k| | |y=\dfrac{a}{x-h}+k| |
| |y=[x]| | |y=a[b(x-h)]+k| | |
| |y=\mid x\ \mid| | |y=a\mid b(x-h) \mid +k| | |y=a\mid x-h \mid +k| |
| |y=\sqrt{x}| | |y=a \sqrt{b(x-h)}+k| | |y=a \sqrt{\pm(x-h)}+k| |
| |y=c^x| | |y=a(c)^{b(x-h)}+k| | |y=a(c)^{x}+k| |
| |y=\log_c x| | |y=a\log_c \big(b(x-h)\big) +k| | |y=\log_c \big(b(x-h)\big)| ou |y=\log_c \big(\pm(x-h)\big) +k| |
| |y=\sin x| | |y=a \sin \big(b(x-h)\big)+k| | |
| |y=\cos x| | |y=a \cos \big(b(x-h)\big)+k| | |
| |y=\tan x| | |y=a \tan \big(b(x-h)\big)+k| |
Dans l'animation suivante, tu peux sélectionner la fonction de ton choix et modifier les paramètres |a,| |b,| |h| et |k| de même que la base |c| pour les fonctions exponentielle et logarithmique. Observe bien les modifications qui s'opèrent sur la courbe transformée par rapport à la fonction de base. Par la suite, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions sur les paramètres additifs |(h| et |k)| et multiplicatifs |(a| et |b).|
Le rôle des paramètres additifs est de déplacer horizontalement ou verticalement une fonction sans en modifier l'allure. On parle généralement de translation ou de glissement.
Le paramètre |h| a pour effet de faire glisser horizontalement une fonction vers la gauche ou vers la droite, tout dépendant de sa valeur.
-
|h<0:| Translation vers la gauche
-
|h>0:| Translation vers la droite
Pour donner la valeur du paramètre |h,| la fonction doit être écrite sous la forme canonique : |y=af\big(b(x-h)\big)+k.| Lorsque c'est le cas, le paramètre |h| est le nombre situé à droite du signe moins dans la parenthèse.
-
Dans |f(x)=(x \color{red}{-} \color{green}{5})^2+1|, |h| vaut |\color{green}{5}| et non |-5|.
-
Dans |g(x)=3(x+8)^2|, on pourrait réécrire la fonction comme suit : |g(x)=3(x\color{red}{-}\color{green}{\text{-}8})^2|. On en conclut que |h| vaut |\color{green}{\text{-}8}| et non |8|.
-
Dans |h(x)=(2x-12)^2|, on pourrait croire que |h=12|, mais la fonction n'est pas en forme canonique, ce qui porte à confusion. Voici les manipulations qu'il faut effectuer : ||\begin{align} h(x) &=(2x-12)^2 \\ &= \big(2(x-6)\big)^2 \\ &= 2^2(x-6)^2 \\ &= 4(x \color{red}{-} \color{green}{6})^2 \end{align}|| |h| vaut donc |\color{green}{6}|.
Dans cet exemple, la forme de base de la fonction valeur absolue a pour équation |f(x)=\mid x\ \mid.| Lorsqu'on ajoute le paramètre |h,| l'équation devient |f(x)=\mid x-h \mid.|
Le paramètre |k| a pour effet de faire glisser une fonction vers le bas ou vers le haut, tout dépendant de sa valeur.
-
|k<0:| Translation vers le bas
-
|k>0:| Translation vers le haut
Dans cet exemple, la forme de base de la fonction valeur absolue a pour équation |f(x)=\mid x \mid.| Lorsqu'on ajoute le paramètre |k,| l'équation devient |f(x)= \mid x \mid +\ k.|
Le rôle des paramètres multiplicatifs est de modifier l'étirement de la fonction et de lui faire subir des réflexions.
Un changement d'échelle dans un plan cartésien est une transformation qui modifie l'allure du graphique.
Une fonction peut subir un changement d'échelle vertical de facteur |a| ou un changement d'échelle horizontal de facteur |\dfrac{1}{b}|.
Lorsque la fonction est étirée à l'horizontale |\leftarrow \cdot \rightarrow| ou à la verticale ↑⋅↓↑⋅↓1b1ba1ba1b1b1b1b1ba1b1b1b1b1b1b1b1b1b1b1b1bb, on peut employer les mots allongement ou dilatation.
Lorsque la fonction est comprimée à l'horizontale |\rightarrow \cdot \leftarrow| ou à la verticale ↓⋅↑↓⋅↑aaxaxaaaaaxaaaaaaa→⋅←→⋅←→⋅←→⋅←→⋅←1b, on peut employer les mots rétrécissement ou contraction.
Le paramètre |a| a pour effet de faire subir un changement d'échelle vertical à une fonction en l'allongeant ou en la rétrécissant, tout dépendant de sa valeur. De plus, si le paramètre |a| est négatif, il fait subir une réflexion par rapport à l'axe des |x| à la fonction. Le changement d'échelle vertical est de facteur |a,| c'est-à-dire que les ordonnées des points sont multipliées par ce dernier.
-
|\mid\, a \mid > 1:| Allongement vertical
-
|0 < \mid a \mid < 1:| Rétrécissement vertical
-
|a < 0:| Réflexion par rapport à l'axe des |x|
Dans cet exemple, la forme de base de l'équation fonction racine carrée est |f(x)=\sqrt{x}| Lorsqu'on ajoute le paramètre |a|, l'équation devient |f(x)=a\sqrt{x}|.
Le paramètre |b| a pour effet de faire subir un changement d'échelle horizontal à la fonction en l'allongeant ou en la rétrécissant, tout dépendant de sa valeur. De plus, si le paramètre |b| est négatif, il fait subir une réflexion par rapport à l'axe des |y| à la fonction. Le changement d'échelle horizontal est de facteur |\dfrac{1}{b},| c'est-à-dire que les abscisses des points sont multipliées par ce dernier.
-
|0 < \mid b \mid < 1:| Allongement horizontal
-
|\mid\ b \mid > 1:| Rétrécissement horizontal
-
|b < 0:| Réflexion par rapport à l'axe des |y|
Dans cet exemple, la forme de base de l'équation d'une fonction racine carrée est |f(x)=\sqrt{x}|. Lorsqu'on ajoute le paramètre |b|, l'équation devient |f(x)=\sqrt{bx}.|
La transformation qui associe un point de la forme canonique d'une fonction à un point de sa forme de base est : ||(x,y) \mapsto \left(\dfrac{x}{b}+h, ay+k \right)||
On prend donc un point |(x,y)| de la forme de la base et, en lui appliquant les paramètres de la forme canonique, on obtient un nouveau point : |\left(\dfrac{x}{b}+h, ay+k \right).|
Soit la fonction quadratique de base d'équation |y=x^2|.
On transforme cette règle pour obtenir la forme canonique : ||y=-3(x+1)^2+12||
(ici, |b=1|)
Soit la table de valeurs et le graphique suivants :
| |x| | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| |y| | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
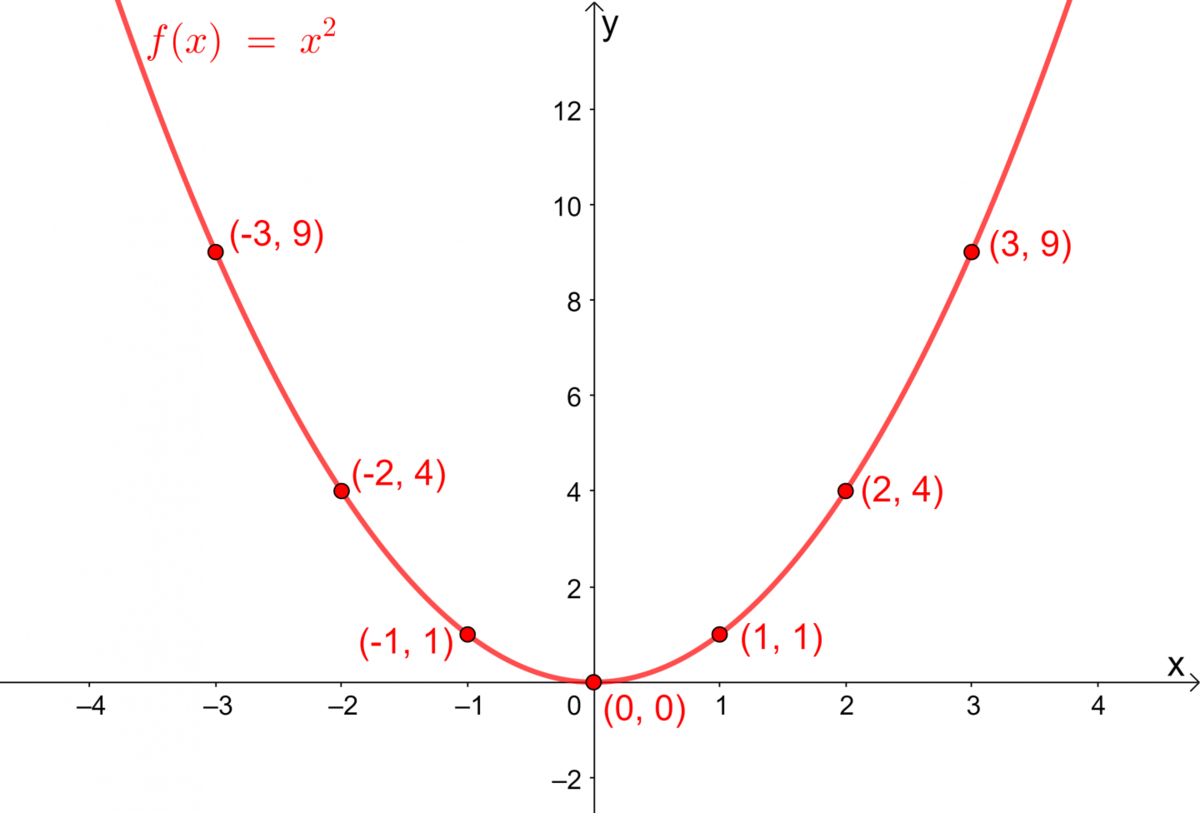
Il faut maintenant appliquer les transformations données par les paramètres selon la règle suivante : |(x,y) \mapsto \left(\dfrac{x}{b}+h, ay+k \right)|
On calcule les coordonnées des nouveaux points |(x', y')| dans le tableau suivant :
| Coordonnées de base | Coordonnées transformées |
|---|---|
| |(x,y)| | |\left(\frac{x}{1}-1,-3y+12\right)| |=(x', y')| |
| |(-3,9)| | |\left(\frac{-3}{1}-1,-3(9)+12\right)| |=(-4,-15)| |
| |(-2,4)| | |\left(\frac{-2}{1}-1,-3(4)+12\right)| |=(-3,0)| |
| |(-1,1)| | |\left(\frac{-1}{1}-1,-3(1)+12\right)| |=(-2,9)| |
| |(0,0)| | |\left(\frac{0}{1}-1,-3(0)+12\right)| |=(-1,12)| |
| |(1,1)| | |\left(\frac{1}{1}-1,-3(1)+12\right)| |=(0, 9)| |
| |(2,4)| | |\left(\frac{2}{1}-1,-3(4)+12\right)| |=(1, 0)| |
| |(3,9)| | |\left(\frac{3}{1}-1,-3(9)+12\right)| |=(2,-15)| |
On peut maintenant tracer les deux courbes dans le graphique ci-contre.
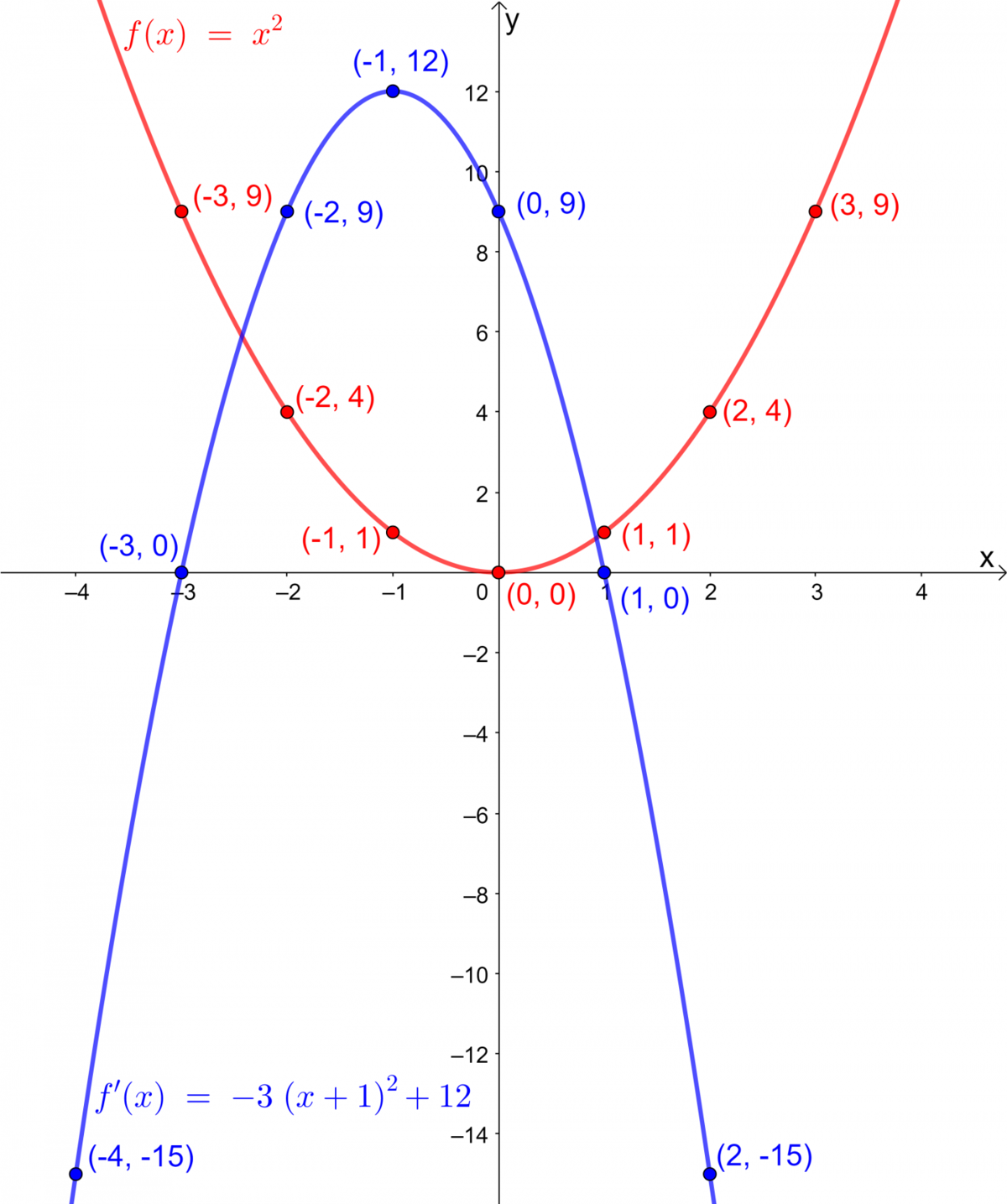
La fonction tracée en rouge correspond à la fonction sous sa forme de base.
La fonction tracée en bleu correspond à la fonction sous sa forme canonique où |a=-3,\ b=1,\ h=-1| et |k=12|. Elle a subi un allongement vertical de facteur 3, une réflexion par rapport à l'axe des |x|, une translation horizontale de 1 unité vers la gauche et une translation verticale de 12 unités vers le haut.
Comment avec l'ajout de paramètres obtient-on la transformation |(x,y) \mapsto \left(\dfrac{x}{b}+h, ay+k \right)|?
Voici une preuve intuitive :
On se donne une fonction transformée |y=af(b(x-h))+k| où |f| est une fonction de base.
On isole la partie |f(b(x-h))|. ||\begin{align}y &= af(b(x-h))+k\\y-k &= af(b(x-h))\\ \frac{y-k}{a} &= f(b(x-h))\end{align}||
Si on pose |Y=\dfrac{y-k}{a}|, on peut isoler |y|.
On obtient d'abord |aY=y-k| et finalement : |y=aY+k|.
Si on pose |X=b(x-h)|, on peut isoler |x|.
On obtient d'abord |\dfrac{X}{b}=x-h| et finalement : |x=\frac{X}{b}+h|.
Il faut simplement ajouter que |X| est la valeur de l'abscisse dans la fonction de base et qu'en appliquant les paramètres, on obtient |x|.
Même chose pour |Y| et |y|.
CQFD