When conducting a survey, it is not always possible to interview every member of a population because of geographical, monetary or time constraints. However, it is still possible to learn about the target population by analyzing a subgroup of the population, called a sample. To do this, it is important to choose the appropriate sampling method to create the sample.
-
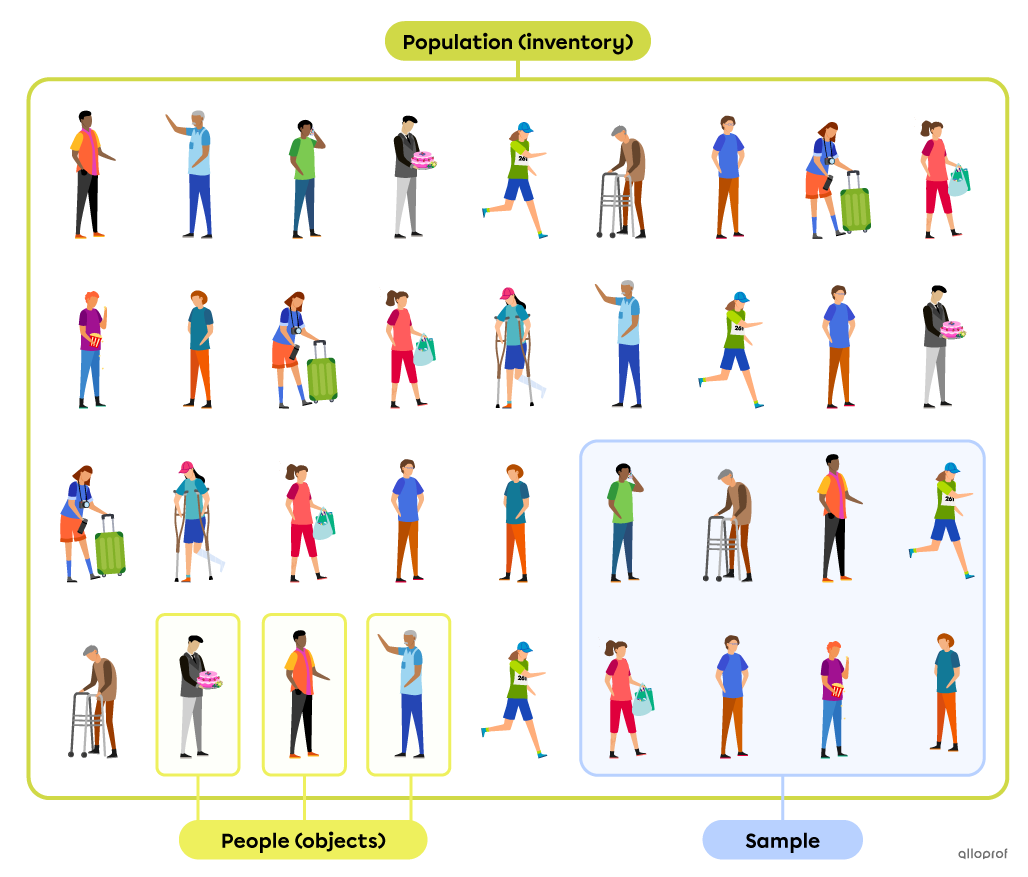
A population is a group made up of all the people about whom information is desired.
-
An inventory is a group of all objects about which information is desired.
-
A sample is a subgroup of people or objects in the population or inventory.
-
A representative sample is a sample that represents the population or inventory as closely as possible in terms of its characteristics and size.
Here is a diagram that illustrates the difference between these terms:
Scientists are interested in the migratory movement of Northern Gannets in Québec. Unfortunately, they cannot observe every single bird of this species. However, the scientists can catch a few birds, fit them with electronic chips, and analyze their movements. This way, they can associate the behaviour of a few birds with that of the entire gannet population in Québec.
-
Population: All the Northern Gannets in Quebec
-
Sample: The few Northern Gannets that will have a microchip
It is necessary to identify the target population as precisely as possible before conducting research. Otherwise, there is a risk of obtaining results that do not apply to the target population.
In the previous example, if we wanted to obtain information on all the Northern Gannets in the world, we would have to create a representative sample. Since the current sample is only composed of Northern Gannets from Quebec, we cannot draw conclusions about all the Northern Gannets in the world. In fact, the birds found in Quebec may have certain behaviours that differ from those found in other places.
Although the census is the most precise method of finding information about a population, a survey is used more often. Here are some situations where a survey is preferred over a census.
-
The population is too large, so the survey requires fewer expenditures (transportation, employees, materials, etc.).
-
Time is limited.
-
The target population is not easily accessible.
There are several methods for creating a representative sample of a population. Depending on the context and the needs of the study, each method has its advantages and disadvantages.
Random sampling is a way of selecting a sample where every person or object in the population has the same probability of being in the sample, since they are all selected by chance.
Advantage
-
A sample created with the random sampling method is generally representative of the population.
Disadvantage
-
It is necessary to have a complete list of the population to draw from at random.
We want to evaluate the satisfaction of |30\ 000| students at a university about the general cleanliness of the campus. To do this, we decide to construct a sample of |2000| students. Then, a computer randomly selects the names of |2000| students from the university's database.
-
Population: the |30\ 000| university students
-
Sample: the |2000| students chosen at random
-
Sampling method: random, since the computer chooses the names by chance
In systematic sampling, each sample element is selected on a regular basis, in a specific order and interval, from within the target population.

Advantages
-
The sample size and sample elements can be determined in advance.
-
The sample is distributed in equal proportions throughout the population.
Disadvantage
-
Since regular intervals are used to select items, it does not guarantee a representative sample.
To check the quality of the product manufactured by an assembly line in a factory, |1| is analyzed each time |100| products leave the production line.
-
Inventory: all the products manufactured in the factory
-
Sample: |1| product out of |100|
-
Sampling method: systematic, since we choose |1| element at each interval of |100,| according to the order of production
In the cluster sampling method, the population is divided into subgroups (clusters) according to a certain characteristic, and then a number of clusters are selected at random. The sample consists of all the people or objects in the selected clusters.

Advantages
-
It is not necessary to have a list of all members of the target population.
-
It is the ideal method for surveying a population that is geographically widespread.
Disadvantages
-
Generally, items in the same cluster have similar characteristics without necessarily being the same as the target population.
-
It is very difficult to predict the sample size since not all clusters have the same number of individuals.
A doctoral student is conducting research on satisfaction with the quality of food offered in Quebec high school cafeterias. Since it is unrealistic to send a questionnaire to every teenager attending high school in Quebec, she randomly selects a number of schools (clusters) to which she sends a questionnaire to be completed by each student.
-
Population: high school students in Quebec
-
Sample: all students attending the selected schools
-
Sampling method: clustered, since the population is separated into clusters (schools), some are randomly selected and all people in the chosen clusters are interviewed
In the stratified sampling method, a characteristic of the target population is used to divide it into strata (subgroups of the population). Members of each stratum are then selected at random, respecting their proportionality in the population.

Advantage
-
This method ensures a fairly good representation of the population because of its proportionality criterion.
Disadvantage
-
A good knowledge of the population is needed to establish the strata to work with.
To maintain this proportionality, the following equation can be used:
|\dfrac{\begin{gather}\text{Size of}\\\text{the stratum}\end{gather}}{\begin{gather}\text{Size of}\\\text{the population}\end{gather}}=\dfrac{\begin{gather}\text{Number of elements chosen}\\\text{in this stratum}\end{gather}}{\begin{gather}\text{Size of}\\\text{the sample}\end{gather}}|
Here is how to construct a sample using the stratified sampling method.
The city councillor wants information about the location of bus stops in a neighbourhood with |5| streets. To do this, he decides to take a random sample of |100| adult residents from the following population.
| Street | Number of residents |
|---|---|
| Tulip | |75| |
| Lilac | |75| |
| Rose | |200| |
| Geranium | |100| |
| Marguerite | |50| |
| Total | |\boldsymbol{500}| |
To meet the criteria for stratified sampling, the following proportions are calculated.
Tulip Street||\begin{align}\dfrac{75}{500}&=\dfrac{?}{100}\\?&=\dfrac{75 \times 100}{500}\\&=15\end{align}||
It is necessary to randomly select |15| residents of Tulip Street.
Rose Street||\begin{align}\dfrac{200}{500}&=\dfrac{?}{100}\\?&=\dfrac{200 \times 100}{500}\\&=40\end{align}||
It is necessary to select |40| residents of Rose Street
Marguerite Street||\begin{align}\dfrac{50}{500}&=\dfrac{?}{100}\\?&=\dfrac{50 \times 100}{500}\\&=10\end{align}||
It is necessary to select |10| residents of Marguerite Street.
Lilac Street||\begin{align}\dfrac{75}{500}&=\dfrac{?}{100}\\?&=\dfrac{75 \times 100}{500}\\&=15\end{align}||
It is necessary to select |15| residents of Lilac Street.
Geranium Street||\begin{align}\dfrac{100}{500}&=\dfrac{?}{100}\\?&=\dfrac{100 \times 100}{500}\\&=20\end{align}||
It is necessary to select |20| residents of Geranium Street.
In total, |15+15+40+20+10 = 100| neighbourhood residents will be interviewed.
To affirm that a sample is representative of a population, it must have the following characteristics:
-
Be of sufficient size in relation to the population.
-
Have the same characteristics as the population.
A researcher wishes to evaluate the number of hours that high school students in Quebec (population) spend on their smartphones. He therefore decided to survey a class of Secondary 2 students in a Montreal school (sample) on this subject.
-
Sample size
This sample is not representative, since the target population corresponds to all high school students in Quebec, or approximately |350\ 000| adolescents. On the other hand, the sample contains only students from one class, approximately |30| adolescents. -
Characteristics of the sample versus those of the population
This sample is not representative because in the population, all students in secondary schools in the province of Quebec are considered. In other words, the sample would have to contain secondary schools from different regions and secondary students from different grade levels.