Lorsqu’on souhaite effectuer une enquête, il n’est pas toujours possible d’interroger chaque membre d’une population à cause de contraintes géographiques, monétaires ou temporelles. Par contre, il est tout de même possible d’en apprendre plus à propos de la population visée en analysant un sous-groupe de la population, appelé échantillon. Pour ce faire, il est important de choisir la bonne méthode pour créer cet échantillon.
-
Une population est un groupe formé de toutes les personnes à propos desquelles on souhaite obtenir de l’information.
-
Un inventaire est un groupe formé de tous les objets à propos desquels on souhaite obtenir de l’information.
-
Un échantillon est un sous-groupe de personnes ou d'objets faisant partie de la population ou de l'inventaire.
-
Un échantillon représentatif est un échantillon qui représente le plus fidèlement possible la population ou l'inventaire par ses caractéristiques et sa taille.
Voici un schéma qui illustre bien la différence entre chacun des termes.
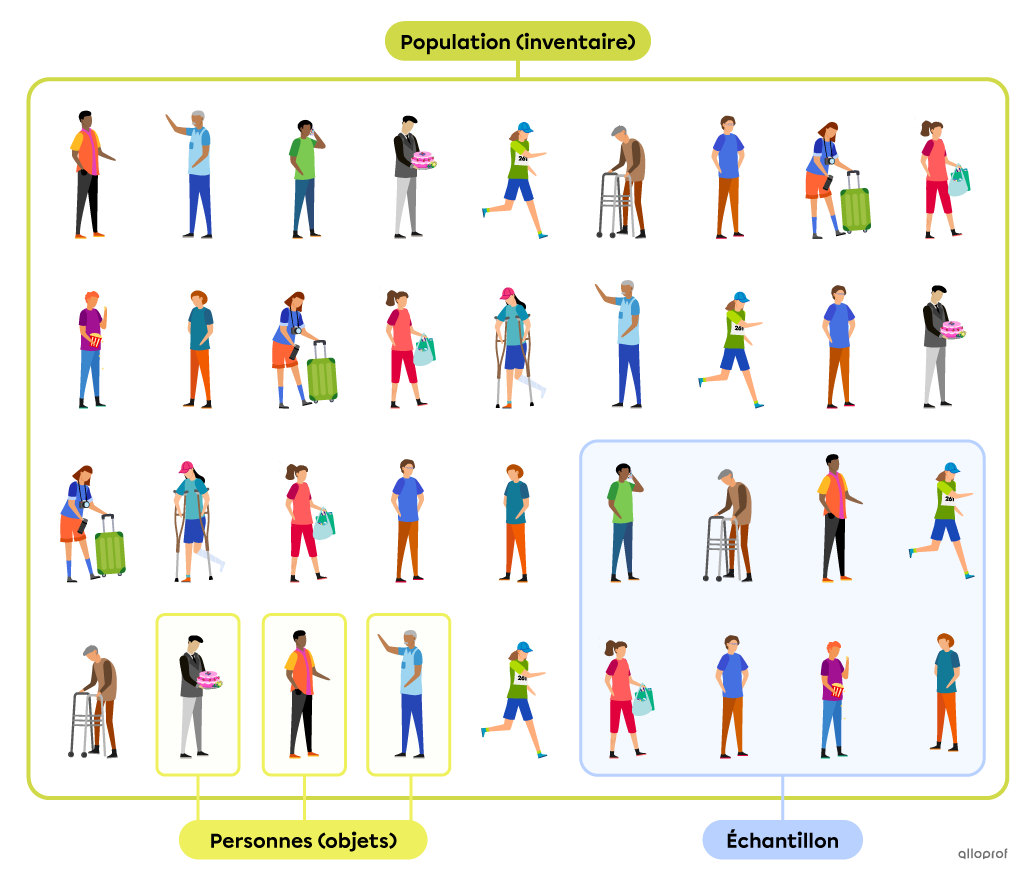
Des scientifiques s’intéressent au mouvement migratoire des Fous de Bassan du Québec. Malheureusement, ils ne peuvent pas observer chacun des oiseaux de cette espèce. Or, les scientifiques peuvent en attraper quelques-uns, leur installer des puces électroniques et analyser leurs déplacements. Ainsi, ils peuvent associer les comportements de ces quelques oiseaux à ceux de toute la population des Fous de Bassan du Québec.
-
Population : tous les Fous de Bassan du Québec
-
Échantillon : les quelques Fous de Bassan qui auront une puce électronique
Il est nécessaire d'identifier le plus précisément possible la population ciblée avant d’effectuer la recherche d’informations. Autrement, on risque d’obtenir des résultats qui ne s’appliquent pas à la population ciblée.
Dans l’exemple précédent, si on voulait obtenir des renseignements sur tous les Fous de Bassan du monde, il aurait fallu créer un échantillon représentatif. Puisque l’échantillon actuel est seulement composé de Fous de Bassan du Québec, on ne peut pas tirer de conclusions sur tous les Fous de Bassan du monde. En effet, les oiseaux qui se trouvent au Québec ont peut-être certains comportements qui diffèrent de ceux provenant d’autres endroits.
Bien que le recensement soit la méthode de recherche d’information la plus précise pour une population, on procède plus souvent à un sondage. Voici quelques situations pour lesquelles on favorise le sondage au recensement.
-
La population est trop grande, donc le sondage engendre moins de dépenses (transport, employés, matériels, etc.).
-
Le temps est limité.
-
La population ciblée est difficilement accessible.
Il existe plusieurs méthodes permettant de créer un échantillon représentatif dans une population. En fonction du contexte et des besoins de l'étude, chaque méthode a ses avantages et ses inconvénients.
L’échantillonnage aléatoire est une façon de choisir un échantillon où chaque personne ou objet de la population a la même probabilité de faire partie de l’échantillon, puisqu'ils sont tous sélectionnés au hasard.
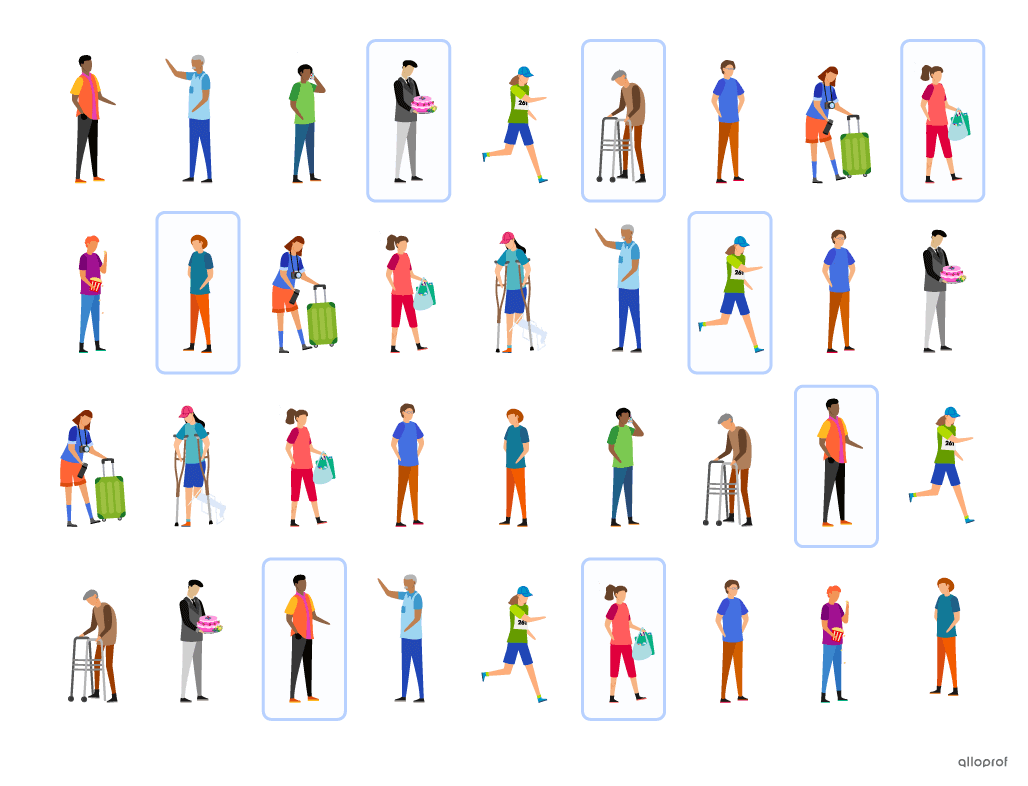
Avantage
-
Un échantillon créé avec la méthode d’échantillonnage aléatoire simple est généralement représentatif de la population.
Inconvénient
-
Il faut avoir la liste complète de la population pour ensuite faire le tirage au sort.
On souhaite évaluer la satisfaction des |30\ 000| étudiants d’une université à propos de la propreté générale du campus. Pour ce faire, on décide de construire un échantillon de |2\ 000| étudiants. Ainsi, un ordinateur choisit au hasard le nom de |2\ 000| d'entre eux à partir de la base de données de l’université.
-
Population : les |30\ 000| étudiants de l’université
-
Échantillon : les |2\ 000| étudiants choisis aléatoirement
-
Méthode d’échantillonnage : aléatoire simple, puisque l’ordinateur choisit les noms au hasard
Dans l’échantillonnage systématique, chaque élément qui compose l'échantillon est choisi de façon régulière, selon un ordre et un intervalle précis, à l'intérieur de la population ciblée.

Avantages
-
On peut déterminer d’avance la taille et les éléments faisant partie de l'échantillon.
-
L'échantillon est distribué dans des proportions égales dans la population.
Inconvénient
-
Puisqu’on utilise des intervalles réguliers pour choisir les éléments, cela ne garantit pas un échantillon représentatif.
Pour vérifier la qualité du produit fabriqué par une chaine de montage dans une usine, on en analyse |1| à chaque fois que |100| produits sortent de la ligne de production.
-
Inventaire : tous les produits fabriqués dans l’usine
-
Échantillon : |1| produit sur |100|
-
Méthode d’échantillonnage : systématique, puisqu’on choisit |1| élément à chaque intervalle de |100,| selon l’ordre de production
Dans la méthode d’échantillonnage par grappes, on divise la population en sous-groupes (grappes) selon une certaine caractéristique, pour ensuite sélectionner un certain nombre de grappes de façon aléatoire. L’échantillon est composé de toutes les personnes ou objets faisant partie des grappes sélectionnées.

Avantages
-
Il n'est pas nécessaire d'avoir une liste de tous les membres de la population ciblée.
-
C’est la méthode idéale pour sonder une population qui est géographiquement étendue.
Inconvénients
-
Généralement, les éléments d'une même grappe possèdent des caractéristiques semblables sans nécessairement être celles de la population ciblée.
-
Il est très difficile de prédire la taille de l'échantillon étant donné que les grappes n'ont pas toutes la même quantité d'individus.
Une étudiante au doctorat effectue une recherche sur la satisfaction de la qualité de la nourriture offerte dans la cafétéria des élèves québécois au secondaire. Puisqu'il est irréaliste d'envoyer un questionnaire à chaque adolescent fréquentant une école secondaire au Québec, elle choisit aléatoirement un certain nombre d’écoles (grappes) auxquelles elle envoie un questionnaire à remplir par chaque élève.
-
Population : les élèves québécois au secondaire
-
Échantillon : tous les élèves fréquentant les écoles choisies
-
Méthode d’échantillonnage : par grappes, puisque la population est séparée en grappes (écoles), qu’on en choisit quelques-unes aléatoirement et qu’on interroge toutes les personnes dans les grappes choisies
Dans la méthode d’échantillonnage stratifié, on se base sur une caractéristique de la population ciblée pour la diviser en strates (sous-groupes de la population). Ensuite, on sélectionne de façon aléatoire des membres de chacune des strates en respectant leur proportionnalité dans la population.

Avantage
-
Cette méthode assure une assez bonne représentativité de la population en raison de son critère de proportionnalité.
Inconvénient
-
Il faut avoir une bonne connaissance de la population afin d'établir les strates avec lesquelles il faut travailler.
Pour conserver cette proportionnalité, on peut utiliser l’égalité suivante.
|\dfrac{\begin{gather}\text{Taille de}\\\text{la strate}\end{gather}}{\begin{gather}\text{Taille de}\\\text{la population}\end{gather}}=\dfrac{\begin{gather}\text{Nombre d'éléments à prendre}\\\text{dans cette strate}\end{gather}}{\begin{gather}\text{Taille de}\\\text{l'échantillon}\end{gather}}|
Voici comment on peut procéder pour construire un échantillon en utilisant la méthode d'échantillonnage par strates.
Le conseiller municipal veut avoir des informations relatives à la localisation des arrêts d'autobus dans un quartier qui compte |5| rues. Pour y arriver, il décide de prélever un échantillon aléatoire de |100| résidents adultes parmi la population suivante.
| Rue | Nombre de résidents |
|---|---|
| Des Tulipes | |75| |
| Des Lilas | |75| |
| Des Rosiers | |200| |
| Des Géraniums | |100| |
| Des Marguerites | |50| |
| Total | |\boldsymbol{500}| |
Pour respecter les critères d'un échantillonnage stratifié, il calcule les proportions suivantes.
Rue des Tulipes||\begin{align}\dfrac{75}{500}&=\dfrac{?}{100}\\?&=\dfrac{75 \times 100}{500}\\&=15\end{align}||Il faut sélectionner aléatoirement |15| résidents de la rue des Tulipes.
Rue des Rosiers||\begin{align}\dfrac{200}{500}&=\dfrac{?}{100}\\?&=\dfrac{200 \times 100}{500}\\&=40\end{align}||Il faut sélectionner |40| résidents de la rue des Rosiers.
Rue des Marguerites||\begin{align}\dfrac{50}{500}&=\dfrac{?}{100}\\?&=\dfrac{50 \times 100}{500}\\&=10\end{align}||Il faut sélectionner|10| résidents de la rue des Marguerites.
Rue des Lilas||\begin{align}\dfrac{75}{500}&=\dfrac{?}{100}\\?&=\dfrac{75 \times 100}{500}\\&=15\end{align}||Il faut sélectionner |15| résidents de la rue des Lilas.
Rue des Géraniums||\begin{align}\dfrac{100}{500}&=\dfrac{?}{100}\\?&=\dfrac{100 \times 100}{500}\\&=20\end{align}||Il faut sélectionner |20| résidents de la rue des Géraniums.
Au total, |15+15+40+20+10 = 100| résidents du quartier seront interrogés.
Pour affirmer qu’un échantillon est représentatif d’une population, il doit avoir les caractéristiques suivantes.
-
Être d'une taille suffisante par rapport à la population.
-
Posséder les mêmes caractéristiques que la population.
Un chercheur souhaite évaluer le nombre d’heures que les élèves des écoles secondaires du Québec (population) passent devant leur téléphone intelligent. Il décide donc d’interroger une classe d'élèves de 2e secondaire d’une école de Montréal (échantillon) à ce sujet.
-
Taille de l'échantillon
Cet échantillon n’est pas représentatif, puisque la population ciblée correspond à tous les élèves québécois de niveau secondaire, soit environ |350\ 000| adolescents. Par contre, l'échantillon contient seulement des élèves d'une classe, soit environ |30| adolescents. -
Caractéristiques de l'échantillon versus celles de la population
Cet échantillon n’est pas représentatif car, dans la population, ce sont tous les élèves des écoles secondaires de la province de Québec qui sont considérés. En d'autres mots, il faudrait que l'échantillon contienne des écoles de différentes régions et des élèves des différentes années du parcours secondaire.