To solve an equation containing an absolute value, refer to its definition.
The absolute value of a real number |x,| denoted |\vert x \vert| , is the following: ||\vert x \vert = \begin{cases} \ \ \ x & \text{if}\ x \geq 0\\ -x & \text{if}\ x < 0\end{cases}||
When an absolute value is isolated on one side of an equality, the algebraic expression or number on the other side must be positive. ||\vert x\vert=\underbrace{\dots}_{\ge\ 0}||
-
If it is a strictly negative number, we stop solving the inequality since there are no solutions.
-
If it is an algebraic expression, then it’s possible to impose a restriction: the value of the algebraic expression must be greater than or equal to |0.|
-
When the absolute value is equal to a positive number ||\vert x+3 \vert = 5||Since |5| is a positive number, this equation has two solutions.
-
When the absolute value is equal to a negative number ||\vert x-4 \vert = -25||Since |-25| is a negative number, this equation has no solution.
-
When the absolute value is equal to an algebraic expression ||\vert 2x-5 \vert = -3x+12||Since the absolute value of |2x-5| is equal to an algebraic expression, this can be positive or negative depending on the value of |x.| Thus, the solutions of this equation are valid if and only if the inequality |-3x+12 \geq 0| is respected. This is a restriction. Thus, |-3x+12 \geq 0| if and only if |x \leq 4.| ||\begin{align} -3x+12 &\geq 0 \\ &\Updownarrow \\ -3x &\geq -12 \\ &\Updownarrow \\ x &\leq 4 \end{align}||In other words, after solving the equation, verify that all the solutions found are less than or equal to |4.|
Here are the steps to solve an equation containing an absolute value.
-
Isolate the absolute value.
-
Check if the absolute value is equal to a positive number and set the restriction, if necessary.
-
Apply the definition of absolute value to form two equations.
-
Solve the two obtained equations.
-
Verify the solutions.
-
Write the solution set.
Solve the equation |\vert 2x + 6 \vert =3.|
-
Isolate the absolute value
The absolute value is already isolated. -
Check if the absolute value is equal to a positive number
Since |3\geq 0,| continue solving the equation. -
Apply the definition of the absolute value to form two equations
||\vert 2x + 6 \vert = 3\ \Leftrightarrow \begin{cases}\! 2x+6=3\\ \quad\text{or} \\ \!2x+6=-3 \end{cases}||
-
Solve the two equations obtained
||\begin{align} 2x+6&=3 \\ 2x&=-3 \\ x_1 &= -\dfrac{3}{2} \end{align}||
||\begin{align} 2x+6&=-3 \\ 2x&=-9 \\ x_2 &= -\dfrac{9}{2} \end{align}||
-
Verify the solutions
||\begin{align} x_1\rightarrow \left\vert 2\! \left(-\dfrac{3}{2}\right) + 6 \right\vert &= \vert 3 \vert = 3 \\\\ x_2\rightarrow \left\vert 2\! \left(- \dfrac{9}{2}\right) + 6 \right\vert &= \vert{-3} \vert = 3 \end{align}||Both solutions are valid.
-
Give the solution set
The solution set is: |x\in \left\lbrace -\dfrac{9}{2},-\dfrac{3}{2} \right\rbrace.|
In step 3, there are two ways to form the two equations.
For example, with the equation |\vert a \vert = b,| it’s possible to form the two equations to solve…
A)
… by changing the sign of the algebraic expression inside the absolute value while keeping the sign of the other side of the equation unchanged. ||\begin{cases} \ \ \, a =b\\ \quad\ \ \text{or} \\ \color{red}{-}a =b \end{cases}||
B)
… by keeping the algebraic expression inside the absolute value unchanged while varying the sign of the other side of the equation. ||\begin{cases}a=b\\ \quad \text{or} \\ a =\color{red}{-}b \end{cases}||
When the absolute value is equal to a number and not an algebraic expression, as in the previous example, it is much easier to choose option B – which is the reason for using this strategy. If option A were chosen, here is what would have been obtained: ||\vert 2x + 6 \vert = 3\\ \Updownarrow\\ \overbrace{\begin{align} \begin{aligned} 2x+6&=3 \\ 2x&=-3 \\ x_1 &= -\dfrac{3}{2} \\ \phantom{x} \end{aligned} \qquad \begin{aligned} -(2x+6)&=3 \\ -2x-6&=3\\-2x&=9 \\ x_2 &= -\dfrac{9}{2} \end{aligned} \end{align}}||The same two solutions are found, regardless of the chosen strategy.
Here is an example where one of the solutions must be rejected.
Solve the equation |\dfrac{1}{2} \vert x+5 \vert = x-2.|
-
Isolate the absolute value ||\begin{align} \dfrac{1}{2} \vert x + 5 \vert \color{#ec0000}{\times 2} &= (x-2) \color{#ec0000}{\times 2} \\ \vert x + 5 \vert &= 2x - 4 \end{align}||
-
Check if the absolute value is equal to a positive number and set the restriction
Since the absolute value is equal to an algebraic expression, a restriction must be imposed on |x.| ||\begin{align} 2x-4 \geq 0 \\ 2x \geq 4 \\ x \geq 2 \end{align}|| -
Apply the definition of absolute value to form two equations ||\vert x+5 \vert = 2x-4\\ \Updownarrow \\ \begin{cases} x+5 = 2x-4 \\ \quad\text{or} \\ -(x+5) = 2x-4 \end{cases}||
-
Solve the two equations obtained
||\begin{align} x+5&=2x-4 \\ -x&=-9 \phantom{()} \\ x_1 &= 9 \end{align}||
||\begin{align} -(x+5)&=2x-4 \\ -x-5&=2x-4 \\ -3x &= 1 \\ x_2 &= -\dfrac{1}{3} \end{align}||
-
Verify the solutions
|x_1=9| respects the restriction since |9\geq 2.| Therefore, it is a solution of the equation.
|x_2=-\dfrac{1}{3}| does not respect the restriction since |-\dfrac{1}{3} \not\geq 2.| Therefore, |-\dfrac{1}{3}| is not part of the solution set.
The graph to the right shows what is happening.
Sketch the absolute value function and the line with the equation |\color{#333fb1}{y=x-2}.|
Point |\left(-\dfrac{1}{3}, -\dfrac{7}{3}\right),| which corresponds to the 2nd solution, is located at the intersection of the line |\color{#333fb1}{y=x-2}| and the extension of the absolute value function’s left branch (not the absolute value function itself).

-
Write the solution set
The only solution of the equation is |x=9.|
There are two ways to verify the solutions found.
-
By making sure that the restrictions are respected, as in the previous example.
-
By substituting the two values of |x| obtained in step 4 in the original equation.
In step 5 of the previous example, the following verification could be done. ||\begin{align} \dfrac{1}{2} \vert \color{#3a9a38}x + 5 \vert &= x-2 \\ x_1 \rightarrow\ \dfrac{1}{2} \vert \color{#3a9a38}{9} + 5 \vert &\overset{?}{=} \color{#3a9a38}{9}-2 \\ 7 &= 7 \\\\ x_2 \rightarrow\ \dfrac{1}{2} \left\vert \color{#3a9a38}{-\dfrac{1}{3}} + 5 \right\vert &\overset{?}{=} \color{#3a9a38}{-\dfrac{1}{3}} -2 \\ \dfrac{7}{3} &\color{#ec0000}{\not=} -\dfrac{7}{3} \end{align}||The solution |-\dfrac{1}{3}| must therefore be rejected.
Here is an example where the equation has no solution.
Solve the equation |3 \vert x - 1 \vert + 6 = 0.|
-
Isolate the absolute value ||\begin{align} 3 \vert x - 1 \vert + 6 &= 0 \\ 3\vert x - 1 \vert &= -6 \\ \vert x - 1 \vert &= -2 \end{align}||
-
Check if the absolute value is equal to a positive number
Stop solving the equation since an absolute value cannot be equal to a negative number. Give the answer directly.
Answer: There is no solution. The solution set is: |x \in \varnothing.|
Note: In the image below, notice how the absolute value function with an equation of |y=3\vert x - 1 \vert + 6| never intersects the horizontal line with the equation |\color{#333fb1}{y=0}.| This explains why the equation |3 \vert x - 1 \vert + 6 = \color{#333fb1}{0}| has no solution.

Here is another example where one of the obtained solutions must be rejected.
Solve the equation |2\vert x - 4 \vert +1 = 3x+2.|
-
Isolate the absolute value ||\begin{align} 2 \vert x - 4 \vert +1 &= 3x+2 \\ 2\vert x -4 \vert &= 3x+1 \\ \vert x -4 \vert &= \dfrac{3x+1}{2} \end{align}||
-
Check if the absolute value is equal to a positive number and set the restriction
Since the absolute value is equal to an algebraic expression, impose a restriction on |x.| ||\begin{align} \dfrac{3x+1}{2} &\geq 0 \\ 3x+1 &\geq 0 \\ 3x &\geq -1 \\ x &\geq \dfrac{-1}{3} \end{align}|| -
Apply the definition of absolute value to form two equations ||\vert x-4 \vert = \dfrac{3x+1}{2}\\ \ \\ \Updownarrow \\ \ \\ \begin{cases} \ \ \ \ \, x-4\,\, =\dfrac{3x+1}{2} \\ \qquad\qquad \text{ou}\\ -(x-4) =\dfrac{3x+1}{2}\ \end{cases}||
-
Solve the two equations obtained
||\begin{align} x-4&=\dfrac{3x+1}{2} \\ 2x-8&=3x+1 \\ -x &= 9 \\ x_1 &= -9\phantom{\dfrac{7}{5}} \end{align}||
||\begin{align} -x+4&=\dfrac{3x+1}{2} \\ -2x+8&=3x+1 \\ -5x &= -7 \\ x_2 &= \dfrac{7}{5} \end{align}||
-
Verify the solutions
|x_1=-9| does not respect the restriction since |-9 \not\geq \dfrac{-1}{3}.| Therefore, |-9| is not part of the solution set.
However, |x_2=\dfrac{7}{5}| respects the restriction since |\dfrac{7}{5} \geq \dfrac{-1}{3}.| -
Write the solution set
The sole solution of this equation is |x=\dfrac{7}{5}.|
To solve an inequality containing an absolute value, it is useful to sketch a graph to determine the solution set.
Here are the main steps to follow.
-
Replace the inequality symbol with the equal symbol.
-
Isolate the absolute value.
-
Check if the absolute value is equal to a positive number and set the restriction, if necessary.
-
Apply the definition of absolute value.
-
Solve the equations.
-
Verify the solutions of the equation formed in step 1.
-
Determine the solution set of the inequality using a graph or a number line.
Solve the inequality |\vert 3 - 2x \vert > 9.|
-
Replace the inequality symbol with an equal symbol ||\vert 3 - 2x \vert = 9||
-
Isolate the absolute value
The absolute value is already isolated. -
Check if the absolute value is equal to a positive number
Since |9\geq 0,| continue to solve the equation. -
Apply the definition of absolute value ||\vert 3-2x \vert = 9\\ \ \\ \Updownarrow \\ \ \\ \begin{cases} 3-2x =9\\ \qquad \text{or} \\ 3-2x =-9 \end{cases}||
-
Solve the equations
||\begin{align} 3-2x&=9 \\ -2x&=6 \\ x_1 &= -3 \end{align}||
||\begin{align} 3-2x&=-9 \\ -2x&=-12 \\ x_2 &= 6 \end{align}||
-
Verify the solutions of the equation formed in step 1
Since there are no restrictions, both solutions are valid and can be verified. ||\begin{align} x_1 &\rightarrow \vert 3-2(\color{#3a9a38}{-3})\vert = \vert 9 \vert = 9 \\ x_2 &\rightarrow \vert 3-2(\color{#3a9a38}{6})\vert = \vert{-9}\vert = 9 \end{align}||The two solutions of the equation are indeed valid. -
Determine the solution set of the inequality using a graph
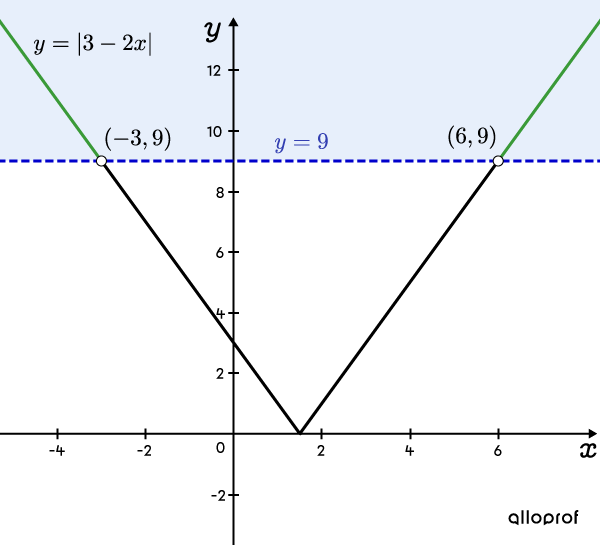
Since the starting inequality is |\vert 3 - 2x \vert > \color{#333fb1}{9},| graphically represent the absolute value function and the horizontal line located at |\color{#333fb1}{y=9}.|
The solution set consists of all parts of the curve lying strictly above |\color{#333fb1}{y=9}.| The intersection points are represented by empty points because they are not above |9,| but at a height equal to |9.|
Answer Using the graph, it can be concluded that the solution set is |x\in\ ]-\infty,-3[\, \cup\, ]6,+\infty[.|
Note: Since the inequality sign is |>,| the interval boundaries are not included.
To determine the solution set (step 7), the following visual aids can be used.
-
A graph of the situation
This option was chosen in the previous example. It is not rare, in word problems, for the graph of the situation to have already been sketched at this stage. If that is the case, the solution set can be quickly determined. -
A number line
Here's what this visual aid would have looked like for the previous example:On a number line, place the solutions found in step 5.
Place empty points if the inequality symbol is |>| or |.|
Place solid points if the inequality symbol is |\geq| or |\leq.|
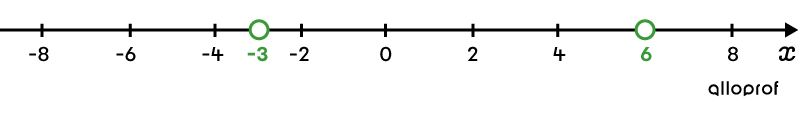
The dots separate the line into three sections: |]-\infty, -3[,| |]-3,6[,| and |]6,\infty[.|
It is necessary to test a random value in each of these sections by verifying it with the initial inequality.
-
For |]-\infty, -3[,| use |x=-5.| ||\begin{align} \vert 3 - 2x \vert &> 9 \\ \vert3-2(-5)| &\overset{?}{>} 9 \\ 13 &> 9 \end{align}||Since the inequality is true, the interval |]-\infty, -3[| is part of the solution set.
-
For |]-3,6[,| use |x=0.| This obtains |3 \not> 9,| so the interval |]-3,6[| is not part of the solution set.
-
For |]6,\infty[,| use |x=10.| This obtains |17>9.| Since the inequality is true, the interval |]6,\infty[| is part of the solution set.
The solution set indeed corresponds to that determined using the graph, which is |x\in\ ]-\infty,-3[\, \cup\, ]6,+\infty[.|
On the number line, colour the sections that correspond to the solution set.
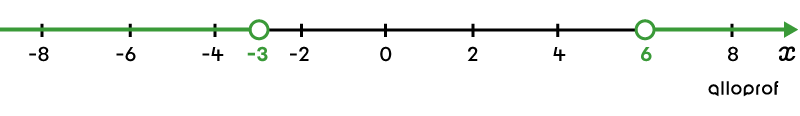
Solve the inequality |\vert 5 - x \vert \leq 3x+1.|
-
Replace the inequality symbol with an equal symbol ||\vert 5 - x \vert = 3x +1||
-
Isolate the absolute value
The absolute value is already isolated. -
Check if the absolute value is equal to a positive number and set the restriction ||\begin{align} 3x+1 &\geq 0 \\ 3x &\geq -1 \\ x &\geq -\dfrac{1}{3} \end{align}||
-
Apply the definition of absolute value ||\vert 5-x \vert = 3x+1\\ \ \\ \Updownarrow \\ \ \\ \begin{cases} \quad 5-x\ \,= 3x+1 \\ \qquad \text{or} \\ -(5-x) =3x+1 \end{cases}||
-
Solve the two equations
||\begin{align} 5-x&=3x+1 \\ -4x&=-4 \\ x_1 &= 1 \end{align}||
||\begin{align} -5+x&=3x+1 \\ -2x&=6 \\ x_2 &= -3 \end{align}||
-
Verify the solutions of the equation formed in step 1
|x_1=1| respects the restriction because |1\geq -\dfrac{1}{3}.|
|x_2=-3| violates the restriction because |-3 \not\geq -\dfrac{1}{3}.|
Thus, |1| is part of the solution set, but |-3| is not part of it. -
Determine the solution set of the inequality using a graph
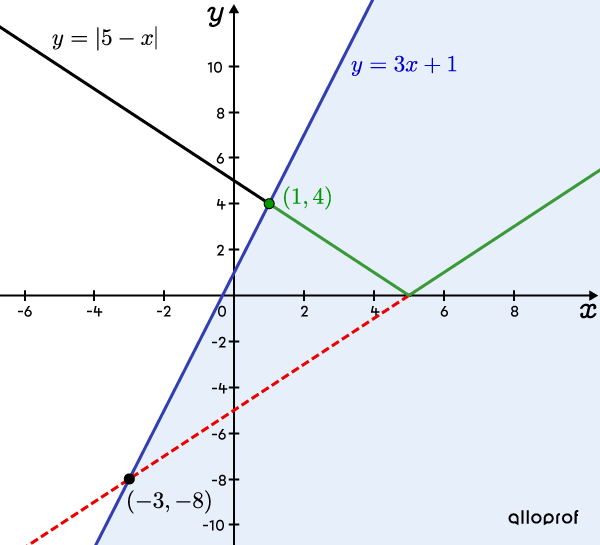
Since the starting inequality is |\vert 5 - x \vert \leq \color{#333fb1}{3x+1},| graphically represent the absolute value function and the linear function |\color{#333fb1}{y=3x+1}.|
The solution set consists of all portions of the curve located below the line |\color{#333fb1}{y=3x+1}.| Also, the point of intersection |\color{#3a9a38}{(1,4)}| is represented by a solid dot. It is part of the solution set because the inequality symbol includes the equality |(\leq).|
Note : The point |(-3,-8)| is just the intersection point between the extension of the right branch of the absolute value and the line |\color{#333fb1}{y=3x+1}.|
Answer: The solution set is |[1,+\infty[.|
Note: The lower boundary |(1)| of the interval is included since the inequality sign is |\leq.|
Two special cases can arise when solving an absolute value inequality.
-
If the absolute value is greater than a negative number, the solution set is |\mathbb{R}.|
-
If the absolute value is less than a negative number, there is no solution.
-
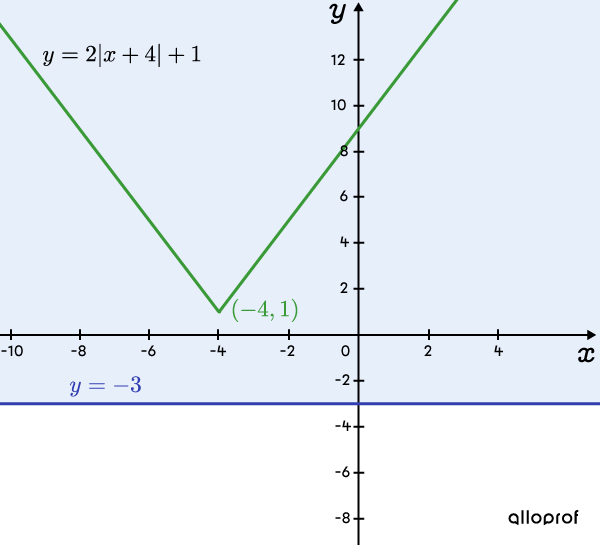
Solve the inequality |2\vert x+4 \vert +1 \geq -3.| ||\begin{align} 2\vert x+4 \vert +1 &\geq -3 \\ 2\vert x+4 \vert &\geq -4 \\ \vert x+4 \vert &\geq -2 \end{align}||This last inequality is always true because an absolute value always gives a number greater than |0.|
Answer: The solution set is |x\in \mathbb{R}.|
In the graph illustrating the initial inequality, just as in that of the reduced inequality, observe how the sketch of the absolute value function is always above the horizontal line for all possible values of |x.|
Graph illustrating the starting inequality ||\boldsymbol{2\vert x+4 \vert +1 \geq -3}||
Graph illustrating the reduced inequality ||\boldsymbol{\vert x+4 \vert \geq -2}||
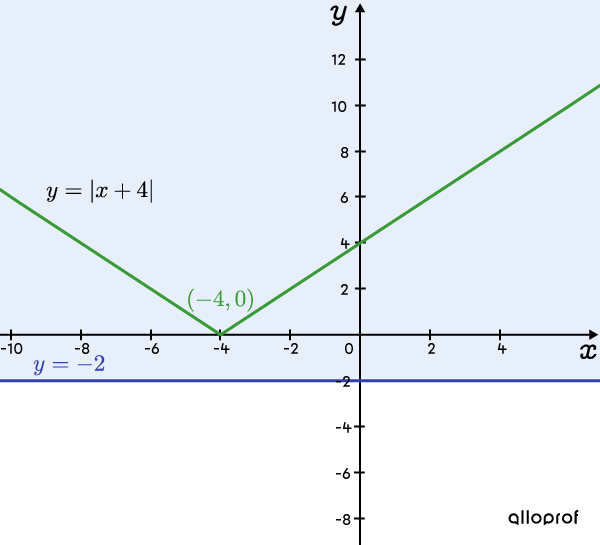
-
Solve the inequality |-\dfrac{1}{2}\vert x+4 \vert +2> 3.| ||\begin{align} -\dfrac{1}{2}\vert x+4 \vert +2 &> 3 \\ \color{#ec0000}{\dfrac{\color{black}{-\frac{1}{2}\vert x+4 \vert}}{-\frac{1}{2}}} &>\ \color{#ec0000}{\dfrac{\color{black}{1}}{-\frac{1}{2}}}\end{align} \\ \qquad\ \underbrace{\vert x+4 \vert < -2}\\ \qquad\ \text{Impossible}||When dividing or multiplying by a negative number, the inequality sign must be reversed. This is why the inequality changed from |>| at |<.|
The resulting inequality is always false because an absolute value is always a number greater than |0.|
Answer: This inequality has no solution. The solution set is |x\in \varnothing.|
Once again, the graph of the starting situation and the graph illustrating the reduced inequality can be sketched to validate the answer.
Graph illustrating the starting inequality ||\boldsymbol{-\dfrac{1}{2}\vert x+4 \vert +2> 3}||
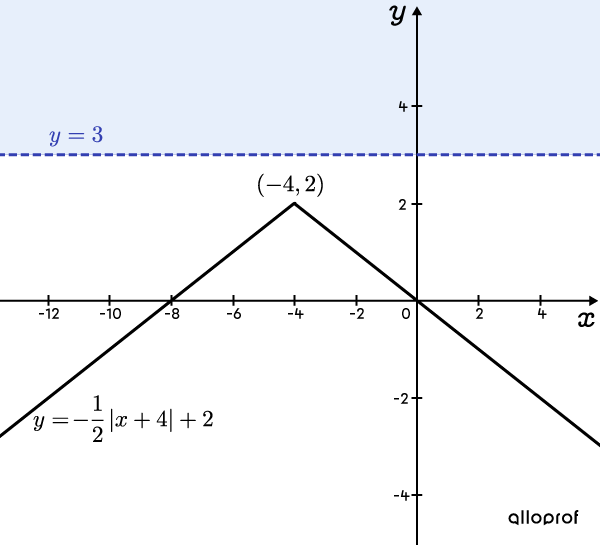
In this graph, we see that the plot of the absolute value function is never above the line |\color{#333fb1}{y=3}.|
The inequality |-\dfrac{1}{2}\vert x+4 \vert +2> 3| is therefore always false and has no solution.
Graph illustrating the reduced inequality ||\boldsymbol{\vert x+4 \vert < -2\phantom{\dfrac{1}{2}}}||
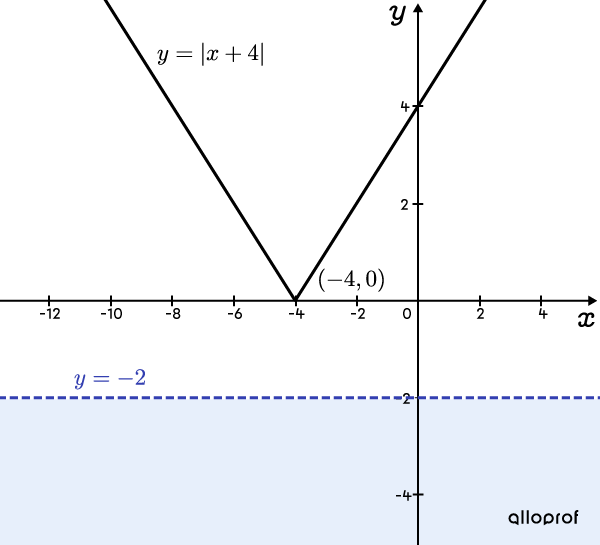
We see that the plot of the absolute value function is never below the horizontal line |\color{#333fb1}{y=-2}.|
The inequality |\vert x+4 \vert < -2| is therefore always false and has no solution. The same is true for the initial inequality from which it derives.
Sometimes, graphing the situation reveals that there is no point of intersection. In that case, the solution set can be given without doing any algebraic calculations.