Pour résoudre une équation contenant une valeur absolue, il faut se référer à sa définition.
La valeur absolue d’un nombre réel |x,| notée |\vert x \vert| est la suivante. ||\vert x \vert = \begin{cases} \ \ \ x & \text{si}\ x \geq 0\\ -x & \text{si}\ x < 0\end{cases}||
Lorsqu’une valeur absolue est isolée d’un côté de l’égalité, l’expression algébrique ou le nombre de l’autre côté doit être positif. ||\vert x\vert=\underbrace{\dots}_{\ge\ 0}||
-
Si c’est un nombre strictement négatif, on arrête la résolution et il n’y a pas de solutions.
-
Si c’est une expression algébrique, on peut alors poser une restriction : la valeur de l’expression algébrique doit être supérieure ou égale à |0.|
-
Lorsque la valeur absolue est égale à un nombre positif ||\vert x+3 \vert = 5||Comme |5| est un nombre positif, cette équation possède 2 solutions.
-
Lorsque la valeur absolue est égale à un nombre négatif ||\vert x-4 \vert = -25||Comme |-25| est un nombre négatif, cette équation ne possède aucune solution.
-
Lorsque la valeur absolue est égale à une expression algébrique ||\vert 2x-5 \vert = -3x+12||Comme la valeur absolue de |2x-5| est égale à une expression algébrique, celle-ci peut être positive ou négative en fonction de la valeur de |x.| Ainsi, les solutions de cette équation sont valides si et seulement si l’inéquation |-3x+12 \geq 0| est respectée. Il s’agit d’une restriction. Or, |-3x+12 \geq 0| si et seulement si |x \leq 4.| ||\begin{align} -3x+12 &\geq 0 \\ &\Updownarrow \\ -3x &\geq -12 \\ &\Updownarrow \\ x &\leq 4 \end{align}||Autrement dit, après avoir terminé la résolution de l’équation, il faut vérifier que toutes les solutions trouvées sont inférieures ou égales à |4.|
Voici les étapes de la démarche à suivre pour résoudre une équation contenant une valeur absolue.
-
Isoler la valeur absolue.
-
Vérifier si la valeur absolue est égale à un nombre positif et poser la restriction au besoin.
-
Appliquer la définition de la valeur absolue pour former 2 équations.
-
Résoudre les 2 équations obtenues.
-
Valider les solutions.
-
Donner l'ensemble-solution.
Résous l'équation |\vert 2x + 6 \vert =3.|
-
Isoler la valeur absolue
La valeur absolue est déjà isolée. -
Vérifier si la valeur absolue est égale à un nombre positif
Puisque |3\geq 0,| on peut poursuivre la résolution de l’équation. -
Appliquer la définition de la valeur absolue pour former 2 équations
||\vert 2x + 6 \vert = 3\ \Leftrightarrow \begin{cases}\! 2x+6=3\\ \quad\text{ou} \\ \!2x+6=-3 \end{cases}||
-
Résoudre les 2 équations obtenues
||\begin{align} 2x+6&=3 \\ 2x&=-3 \\ x_1 &= -\dfrac{3}{2} \end{align}||
||\begin{align} 2x+6&=-3 \\ 2x&=-9 \\ x_2 &= -\dfrac{9}{2} \end{align}||
-
Valider les solutions
||\begin{align} x_1\rightarrow \left\vert 2\! \left(-\dfrac{3}{2}\right) + 6 \right\vert &= \vert 3 \vert = 3 \\\\ x_2\rightarrow \left\vert 2\! \left(- \dfrac{9}{2}\right) + 6 \right\vert &= \vert{-3} \vert = 3 \end{align}||Les deux solutions sont valides.
-
Donner l'ensemble-solution
L'ensemble-solution est donc |x\in \left\lbrace -\dfrac{9}{2},-\dfrac{3}{2} \right\rbrace.|
À l’étape 3, il y a 2 façons de former les 2 équations.
Par exemple, avec l’équation |\vert a \vert = b,| on peut former les 2 équations à résoudre…
A)
… en faisant varier le signe de l’expression algébrique qui est dans la valeur absolue tout en gardant inchangé l’autre membre de l'équation. ||\begin{cases} \ \ \, a =b\\ \quad\ \ \text{ou} \\ \color{red}{-}a =b \end{cases}||
B)
… en gardant inchangée l’expression algébrique qui est dans la valeur absolue tout en faisant varier le signe de l’autre membre de l’équation. ||\begin{cases}a=b\\ \quad \text{ou} \\ a =\color{red}{-}b \end{cases}||
Lorsque la valeur absolue est égale à un nombre et non à une expression algébrique, comme c’est le cas dans l’exemple précédent, il est beaucoup plus simple de choisir l’option B et c’est pourquoi c’est la stratégie qui a été retenue. Si on avait choisi l’option A, voici ce qu’on aurait obtenu. ||\vert 2x + 6 \vert = 3\\ \Updownarrow\\ \overbrace{\begin{align} \begin{aligned} 2x+6&=3 \\ 2x&=-3 \\ x_1 &= -\dfrac{3}{2} \\ \phantom{x} \end{aligned} \qquad \begin{aligned} -(2x+6)&=3 \\ -2x-6&=3\\-2x&=9 \\ x_2 &= -\dfrac{9}{2} \end{aligned} \end{align}}||On obtient les 2 mêmes solutions, peu importe la stratégie choisie.
Voici un exemple où on doit rejeter l’une des solutions obtenues.
Résous l'équation |\dfrac{1}{2} \vert x+5 \vert = x-2.|
-
Isoler la valeur absolue ||\begin{align} \dfrac{1}{2} \vert x + 5 \vert \color{#ec0000}{\times 2} &= (x-2) \color{#ec0000}{\times 2} \\ \vert x + 5 \vert &= 2x - 4 \end{align}||
-
Vérifier si la valeur absolue est égale à un nombre positif et poser la restriction
Puisque la valeur absolue est égale à une expression algébrique, on doit poser une restriction à |x.| ||\begin{align} 2x-4 \geq 0 \\ 2x \geq 4 \\ x \geq 2 \end{align}|| -
Appliquer la définition de la valeur absolue pour former 2 équations ||\vert x+5 \vert = 2x-4\\ \Updownarrow \\ \begin{cases} x+5 = 2x-4 \\ \quad\text{ou} \\ -(x+5) = 2x-4 \end{cases}||
-
Résoudre les 2 équations obtenues
||\begin{align} x+5&=2x-4 \\ -x&=-9 \phantom{()} \\ x_1 &= 9 \end{align}||
||\begin{align} -(x+5)&=2x-4 \\ -x-5&=2x-4 \\ -3x &= 1 \\ x_2 &= -\dfrac{1}{3} \end{align}||
-
Valider les solutions
|x_1=9| respecte la restriction puisque |9\geq 2.| Il s’agit donc d’une solution de l’équation.
|x_2=-\dfrac{1}{3}| ne respecte pas la restriction puisque |-\dfrac{1}{3} \not\geq 2.| |-\dfrac{1}{3}| ne fait donc pas partie de l’ensemble-solution.
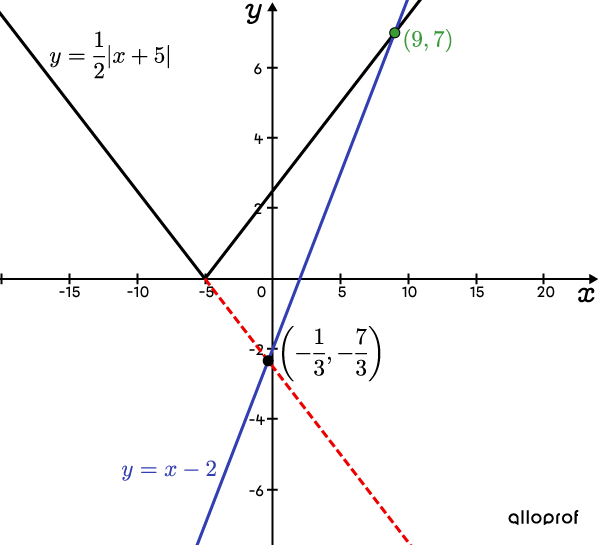
Le graphique ci-contre permet de bien visualiser ce qui se passe.
On trace la fonction valeur absolue ainsi que la droite d’équation |\color{#333fb1}{y=x-2}.|
Le point |\left(-\dfrac{1}{3}, -\dfrac{7}{3}\right),| qui correspond à la 2e solution, est situé à l’intersection de la droite |\color{#333fb1}{y=x-2}| et du prolongement de la branche de gauche de la fonction valeur absolue et non la fonction valeur absolue elle-même.
-
Donner l'ensemble-solution
La seule solution de l’équation est donc |x=9.|
Il y a 2 façons de valider les solutions obtenues.
-
En s'assurant que les restrictions soient respectées, comme dans l’exemple précédent.
-
En substituant les 2 valeurs de |x| obtenues à l’étape 4 dans l’équation de départ.
Dans l’exemple précédent, à l’étape 5, on aurait pu faire la validation suivante. ||\begin{align} \dfrac{1}{2} \vert \color{#3a9a38}x + 5 \vert &= x-2 \\ x_1 \rightarrow\ \dfrac{1}{2} \vert \color{#3a9a38}{9} + 5 \vert &\overset{?}{=} \color{#3a9a38}{9}-2 \\ 7 &= 7 \\\\ x_2 \rightarrow\ \dfrac{1}{2} \left\vert \color{#3a9a38}{-\dfrac{1}{3}} + 5 \right\vert &\overset{?}{=} \color{#3a9a38}{-\dfrac{1}{3}} -2 \\ \dfrac{7}{3} &\color{#ec0000}{\not=} -\dfrac{7}{3} \end{align}||On doit bel et bien rejeter la solution |-\dfrac{1}{3}.|
Voici un exemple où l’équation ne possède aucune solution.
Résous l'équation |3 \vert x - 1 \vert + 6 = 0.|
-
Isoler la valeur absolue ||\begin{align} 3 \vert x - 1 \vert + 6 &= 0 \\ 3\vert x - 1 \vert &= -6 \\ \vert x - 1 \vert &= -2 \end{align}||
-
Vérifier si la valeur absolue est égale à un nombre positif
On arrête la résolution ici puisqu'une valeur absolue ne peut pas être égale à un nombre négatif. On peut donner la réponse directement.
Réponse : Il n’y a aucune solution. L'ensemble-solution est : |x \in \varnothing.|
Remarque : Dans l’image ci-dessous, on voit que la fonction valeur absolue d’équation |y=3\vert x - 1 \vert + 6| ne croise jamais la droite horizontale d’équation |\color{#333fb1}{y=0}.| C’est ce qui explique que l’équation |3 \vert x - 1 \vert + 6 = \color{#333fb1}{0}| ne possède aucune solution.

Voici un autre exemple où on doit rejeter une des solutions obtenues.
Résous l'équation |2\vert x - 4 \vert +1 = 3x+2.|
-
Isoler la valeur absolue ||\begin{align} 2 \vert x - 4 \vert +1 &= 3x+2 \\ 2\vert x -4 \vert &= 3x+1 \\ \vert x -4 \vert &= \dfrac{3x+1}{2} \end{align}||
-
Vérifier si la valeur absolue est égale à un nombre positif et poser la restriction
Puisque la valeur absolue est égale à une expression algébrique, on doit poser une restriction à |x.| ||\begin{align} \dfrac{3x+1}{2} &\geq 0 \\ 3x+1 &\geq 0 \\ 3x &\geq -1 \\ x &\geq \dfrac{-1}{3} \end{align}|| -
Appliquer la définition de la valeur absolue pour former 2 équations ||\vert x-4 \vert = \dfrac{3x+1}{2}\\ \ \\ \Updownarrow \\ \ \\ \begin{cases} \ \ \ \ \, x-4\,\, =\dfrac{3x+1}{2} \\ \qquad\qquad \text{ou}\\ -(x-4) =\dfrac{3x+1}{2}\ \end{cases}||
-
Résoudre les 2 équations obtenues
||\begin{align} x-4&=\dfrac{3x+1}{2} \\ 2x-8&=3x+1 \\ -x &= 9 \\ x_1 &= -9\phantom{\dfrac{7}{5}} \end{align}||
||\begin{align} -x+4&=\dfrac{3x+1}{2} \\ -2x+8&=3x+1 \\ -5x &= -7 \\ x_2 &= \dfrac{7}{5} \end{align}||
-
Valider les solutions
|x_1=-9| ne respecte pas la restriction puisque |-9 \not\geq \dfrac{-1}{3}.| |-9| ne fait donc pas partie de l’ensemble-solution.
Au contraire, |x_2=\dfrac{7}{5}| respecte la restriction puisque |\dfrac{7}{5} \geq \dfrac{-1}{3}.| -
Donner l'ensemble-solution
L’unique solution de cette équation est |x=\dfrac{7}{5}.|
Pour résoudre une inéquation contenant une valeur absolue, il est utile de tracer un graphique afin de déterminer l'ensemble-solution.
Voici les principales étapes à suivre.
-
Remplacer le symbole d'inégalité par le symbole d'égalité.
-
Isoler la valeur absolue.
-
Vérifier si la valeur absolue est égale à un nombre positif et poser la restriction au besoin.
-
Appliquer la définition de la valeur absolue.
-
Résoudre les équations.
-
Valider les solutions de l’équation formée à l’étape 1.
-
Déterminer l’ensemble-solution de l’inéquation à l’aide d’un graphique ou d’une droite numérique.
Résous l’inéquation |\vert 3 - 2x \vert > 9.|
-
Remplacer le symbole d'inégalité par le symbole d'égalité ||\vert 3 - 2x \vert = 9||
-
Isoler la valeur absolue
La valeur absolue est déjà isolée. -
Vérifier si la valeur absolue est égale à un nombre positif
Puisque |9\geq 0,| on peut poursuivre la résolution de l’équation. -
Appliquer la définition de la valeur absolue ||\vert 3-2x \vert = 9\\ \ \\ \Updownarrow \\ \ \\ \begin{cases} 3-2x =9\\ \qquad \text{ou} \\ 3-2x =-9 \end{cases}||
-
Résoudre les équations
||\begin{align} 3-2x&=9 \\ -2x&=6 \\ x_1 &= -3 \end{align}||
||\begin{align} 3-2x&=-9 \\ -2x&=-12 \\ x_2 &= 6 \end{align}||
-
Valider les solutions de l’équation formée à l’étape 1
Comme il n’y a pas de restrictions, les 2 solutions sont valides. On peut le vérifier. ||\begin{align} x_1 &\rightarrow \vert 3-2(\color{#3a9a38}{-3})\vert = \vert 9 \vert = 9 \\ x_2 &\rightarrow \vert 3-2(\color{#3a9a38}{6})\vert = \vert{-9}\vert = 9 \end{align}||Les 2 solutions de l’équation trouvées sont bel et bien valides. -
Déterminer l’ensemble-solution de l’inéquation à l’aide d’un graphique
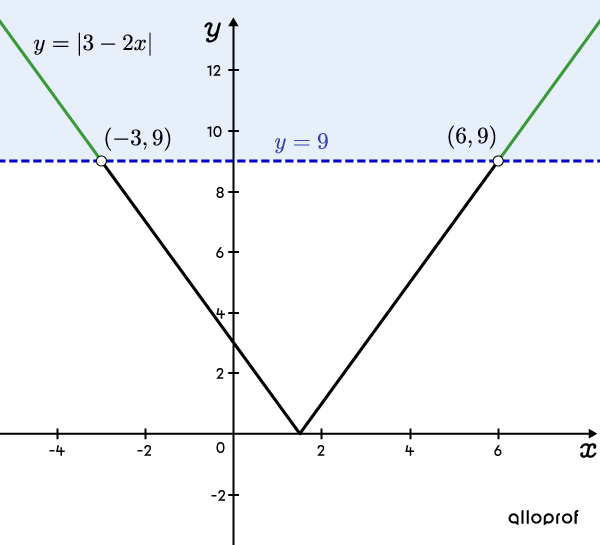
Comme l’inéquation de départ est |\vert 3 - 2x \vert > \color{#333fb1}{9},| on représente graphiquement le tracé d’une fonction valeur absolue et celui d’une droite horizontale située à |\color{#333fb1}{y=9}.|
L’ensemble-solution est constitué de toutes les portions de la courbe situées strictement au-dessus de |\color{#333fb1}{y=9}.| D’ailleurs, les points d’intersection sont représentés par des points vides, car ils ne sont pas au-dessus de |9,| mais bien à une hauteur égale à |9.|
Réponse : Grâce au graphique, on peut conclure que l'ensemble-solution est |x\in\ ]-\infty,-3[\, \cup\, ]6,+\infty[.|
Remarque : Puisque le signe d'inégalité est |>,| les bornes des intervalles ne sont pas incluses.
Pour déterminer l’ensemble-solution (étape 7), on peut avoir recours à l’un ou l’autre des supports visuels suivants.
-
Un graphique de la situation
C’est cette option qui a été choisie dans l’exemple précédent. Il n’est pas rare, dans les problèmes écrits, que le graphique de la situation ait déjà été tracé lorsqu’on arrive à cette étape. Si c’est le cas, on peut donner rapidement l’ensemble-solution. -
Une droite numérique
Voici ce que cela aurait donné pour l’exemple précédent.Sur une droite numérique, on place les solutions trouvées à l’étape 5.
On place des points vides si le symbole d’inégalité est |>| ou |<.|
On place des points pleins si le symbole d’inégalité est |\geq| ou |\leq.|
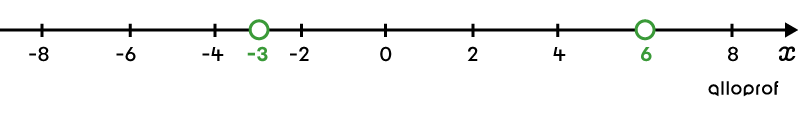
Les points séparent la droite en 3 sections : |]-\infty, -3[,| |]-3,6[| et |]6,\infty[.|
Il faut donc valider une valeur au hasard dans chacune de ces sections dans l’inéquation de départ.
-
Pour |]-\infty, -3[,| on utilise |x=-5.| ||\begin{align} \vert 3 - 2x \vert &> 9 \\ \vert3-2(-5)| &\overset{?}{>} 9 \\ 13 &> 9 \end{align}||Comme l’inégalité est vraie, l’intervalle |]-\infty, -3[| fait partie de l’ensemble-solution.
-
Pour |]-3,6[,| on utilise |x=0.| On obtient |3 \not> 9,| l’intervalle |]-3,6[| ne fait pas partie de l’ensemble-solution.
-
Pour |]6,\infty[,| on utilise |x=10.| On obtient |17>9.| Comme l’inégalité est vraie, l’intervalle |]6,\infty[| fait partie de l’ensemble-solution.
L’ensemble-solution correspond bel et bien à celle déterminée à l’aide du graphique, soit |x\in\ ]-\infty,-3[\, \cup\, ]6,+\infty[.|
Sur la droite numérique, on peut colorier les sections qui correspondent à l’ensemble-solution.
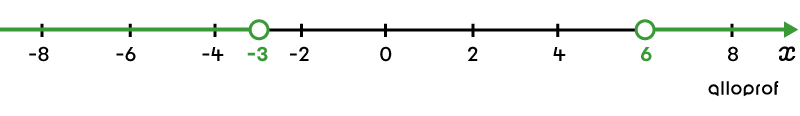
Résous l’inéquation |\vert 5 - x \vert \leq 3x+1.|
-
Remplacer le symbole d'inégalité par le symbole d'égalité ||\vert 5 - x \vert = 3x +1||
-
Isoler la valeur absolue
La valeur absolue est déjà isolée. -
Vérifier si la valeur absolue est égale à un nombre positif et poser la restriction ||\begin{align} 3x+1 &\geq 0 \\ 3x &\geq -1 \\ x &\geq -\dfrac{1}{3} \end{align}||
-
Appliquer la définition de la valeur absolue ||\vert 5-x \vert = 3x+1\\ \ \\ \Updownarrow \\ \ \\ \begin{cases} \quad 5-x\ \,= 3x+1 \\ \qquad \text{ou} \\ -(5-x) =3x+1 \end{cases}||
-
Résoudre les deux équations
||\begin{align} 5-x&=3x+1 \\ -4x&=-4 \\ x_1 &= 1 \end{align}||
||\begin{align} -5+x&=3x+1 \\ -2x&=6 \\ x_2 &= -3 \end{align}||
-
Valider les solutions de l’équation formée à l’étape 1
|x_1=1| respecte la restriction, car |1\geq -\dfrac{1}{3}.|
|x_2=-3| ne respecte pas la restriction, car |-3 \not\geq -\dfrac{1}{3}.|
Ainsi, |1| fait partie de l’ensemble-solution, mais |-3| n’en fait pas partie. -
Déterminer l’ensemble-solution de l’inéquation à l’aide d’un graphique
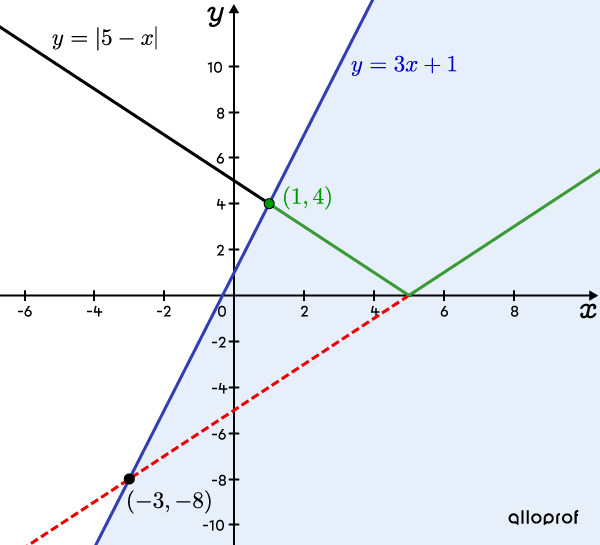
Comme l’inéquation de départ est |\vert 5 - x \vert \leq \color{#333fb1}{3x+1},| on représente graphiquement le tracé d’une fonction valeur absolue et celui de la fonction affine |\color{#333fb1}{y=3x+1}.|
L’ensemble-solution est constitué de toutes les portions de la courbe situées sous la droite |\color{#333fb1}{y=3x+1}.| Aussi, le point d’intersection |\color{#3a9a38}{(1,4)}| est représenté par un point plein. Il fait partie de l’ensemble-solution, car le symbole d’inéquation comprend l’égalité |(\leq).|
Remarque : Le point |(-3,-8)| n’est que le point de rencontre entre le prolongement de la branche de droite de la valeur absolue et la droite |\color{#333fb1}{y=3x+1}.|
Réponse : L'ensemble-solution est |[1,+\infty[.|
Remarque : La borne inférieure |(1)| de l’intervalle est incluse puisque le signe d'inégalité est |\leq.|
Lorsqu’on résout une inéquation valeur absolue, 2 cas particuliers peuvent se présenter.
-
Si la valeur absolue est supérieure à un nombre négatif, l’ensemble-solution est |\mathbb{R}.|
-
Si la valeur absolue est inférieure à un nombre négatif, il n’y a aucune solution.
-
Résous l’inéquation |2\vert x+4 \vert +1 \geq -3.| ||\begin{align} 2\vert x+4 \vert +1 &\geq -3 \\ 2\vert x+4 \vert &\geq -4 \\ \vert x+4 \vert &\geq -2 \end{align}||Cette dernière inéquation est toujours vraie, car une valeur absolue donne toujours un nombre plus grand que |0.|
Réponse : L’ensemble-solution est |x\in \mathbb{R}.|
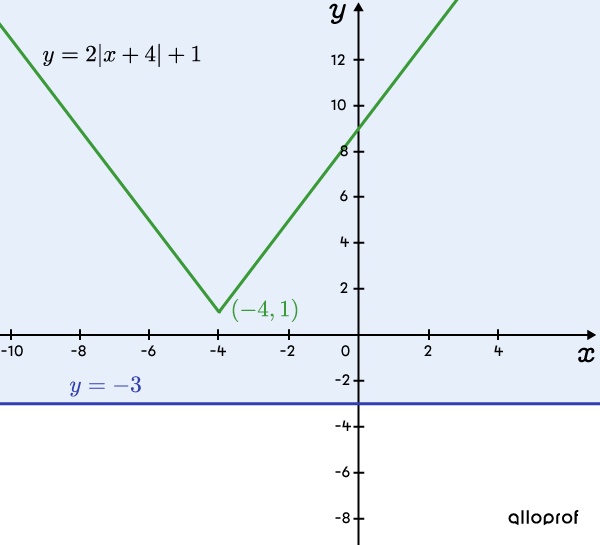
Dans le graphique qui illustre l’inéquation de départ, tout comme dans celui de l’inéquation réduite, on voit que le tracé de la fonction valeur absolue est toujours au-dessus de la droite horizontale pour toutes les valeurs possibles de |x.|
Graphique illustrant l’inéquation de départ ||\boldsymbol{2\vert x+4 \vert +1 \geq -3}||
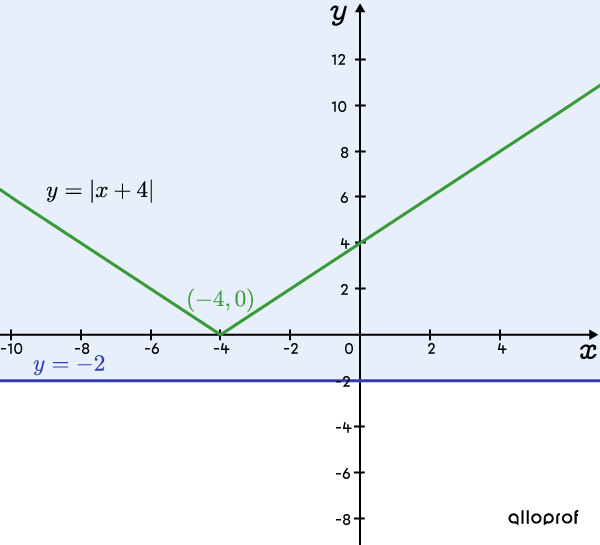
Graphique illustrant l’inéquation réduite ||\boldsymbol{\vert x+4 \vert \geq -2}||
-
Résous l’inéquation |-\dfrac{1}{2}\vert x+4 \vert +2> 3.| ||\begin{align} -\dfrac{1}{2}\vert x+4 \vert +2 &> 3 \\ \color{#ec0000}{\dfrac{\color{black}{-\frac{1}{2}\vert x+4 \vert}}{-\frac{1}{2}}} &>\ \color{#ec0000}{\dfrac{\color{black}{1}}{-\frac{1}{2}}}\end{align} \\ \qquad\ \underbrace{\vert x+4 \vert < -2}\\ \qquad\ \text{Impossible}||Lorsqu’on divise ou qu’on multiplie par un nombre négatif, on doit inverser le signe d’inégalité. C’est pourquoi le signe d’inégalité est passé de |>| à |<.|
L’inéquation obtenue est toujours fausse, car une valeur absolue renvoie toujours un nombre plus grand que |0.|
Réponse : Cette inéquation n’a aucune solution. L’ensemble-solution est |x\in \varnothing.|
Encore une fois, on peut tracer autant le graphique de la situation de départ que celui qui illustre l’inéquation réduite pour valider la réponse.
Graphique illustrant l’inéquation de départ ||\boldsymbol{-\dfrac{1}{2}\vert x+4 \vert +2> 3}||
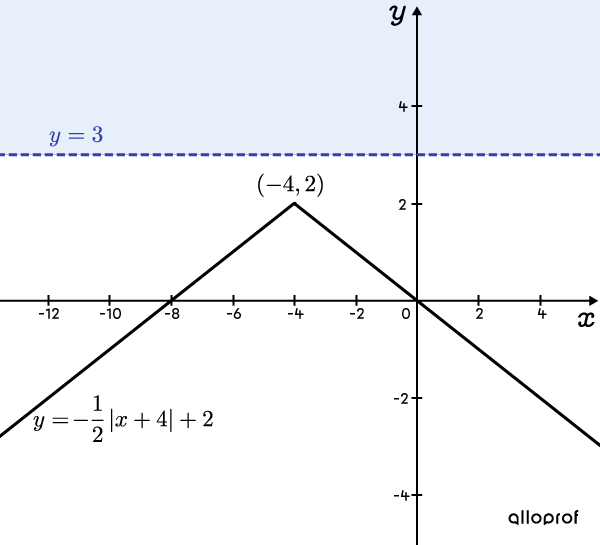
Dans ce graphique, on voit que le tracé de la fonction valeur absolue n’est jamais au-dessus de la droite |\color{#333fb1}{y=3}.|
L’inéquation |-\dfrac{1}{2}\vert x+4 \vert +2> 3| est donc toujours fausse et n’a aucune solution.
Graphique illustrant l’inéquation réduite ||\boldsymbol{\vert x+4 \vert < -2\phantom{\dfrac{1}{2}}}||
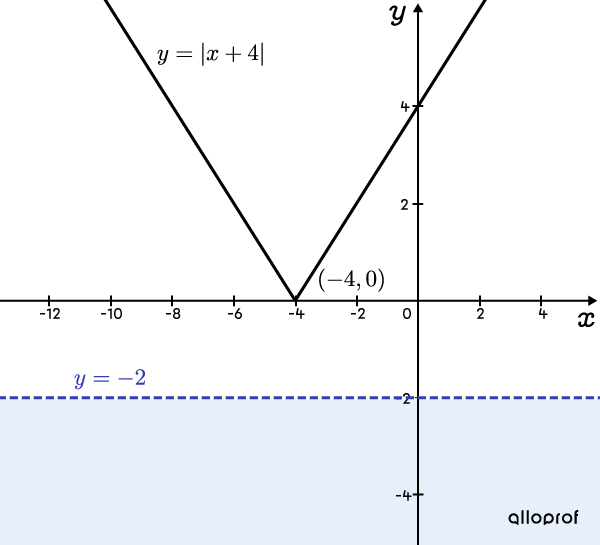
On voit que le tracé de la fonction valeur absolue n’est jamais en dessous de la droite horizontale |\color{#333fb1}{y=-2}.|
L’inéquation |\vert x+4 \vert < -2| est donc toujours fausse et n’a aucune solution. Il en est de même pour l’inéquation de départ dont elle découle.
Parfois, faire le graphique de la situation permet de constater qu’il n’y a aucun point d’intersection. On peut alors donner l’ensemble-solution sans faire le moindre calcul algébrique.