To solve a problem involving a square root function, it is important to understand all the inner workings of the function.
An experiment on falling objects is conducted. After several attempts, it becomes clear that the relationship between the time it takes for an object to reach the ground and the height from which it is released is a square root function. In all of the tests, air resistance was negligible.
a) If the object is thrown from the top of the Empire State Building in New York, which has a height of |381\ \text{m}|, and air resistance is negligible, how long will the fall be?
b) If the object is thrown from the top of the Cliffs of Moher, a beautiful Irish cliff, and the object takes |6.61\ \text{sec}| to hit the water, what was the height of the cliff?
Here is a graph which illustrates the first results of the experiment.
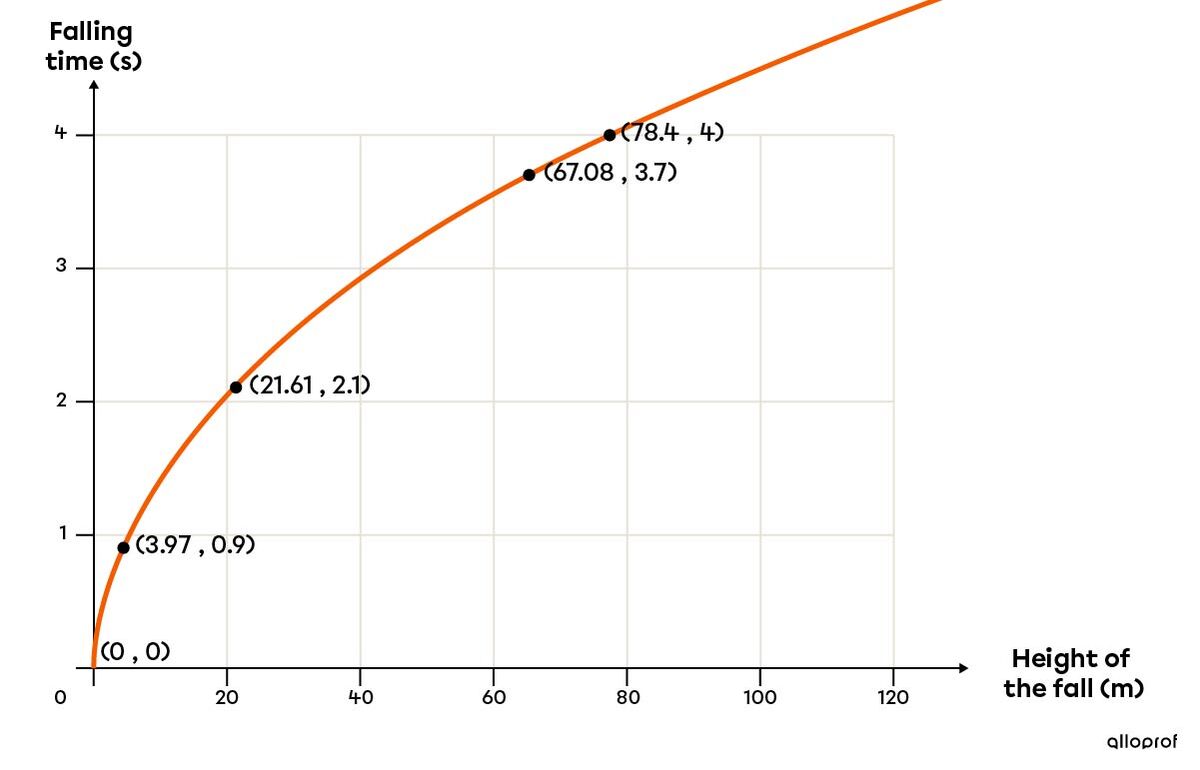
1. Define the variables
|x|: Height of the fall (m)
|f(x)|: Falling time (s)
2. Find the equation
Since the function’s vertex is the point |(0,0)|, use the following equation. ||f(x)=a\sqrt{bx}||
Since the function is located to the right of its vertex, the parameter |b| is positive. ||\begin{align} f(x)=a\sqrt{bx}\quad &\Rightarrow \quad f(x)=a\sqrt{\color{red}{\pm} x}\\ &\Rightarrow \quad f(x)=a\sqrt{ x} \end{align}||
To find the parameter |a|, replace |x| and |f(x)| by the coordinates of a point. Use the point |(78.4, 4).| ||\begin{align} f(x) &= a\sqrt x \\ 4 &= a\sqrt{78.4} \\ 4 &= a(8.85...) \\ 0.452 &\approx a \\\\ \text{The equation is: }f(x) &=0.452\sqrt{x} \end{align}.||
3. Calculate |f(381)|, let |f(x)| when |x=381|
||\begin{align} f(x) &= 0.452\sqrt x \\ f(381) &= 0.452\sqrt{381} \\ &\approx 8.82\ \text{s} \\ \end{align}||
4. Calculate |x| when |f(x)=6.61|
||\begin{align} f(x) &= 0.452\sqrt x \\ 6.61 &= 0.452\sqrt{x} \\ \frac{6.61}{\color{red}{0.452}} &= \frac{0.452}{\color{red}{0.452}}\sqrt x \\ 14.62 &\approx \sqrt x \\ 14.62^2 &\approx (\sqrt{x})^2 \\ 214\ \text{m} &\approx \ x \end{align}||
ANSWERS
a) If an object falls from the top of the Empire State Building, the fall will last approximately |8.82\ \text{sec}.|
b) The Cliffs of Moher have an approximate height of |214\ \text{m}.|
The next example addresses the concept of free fall and linear motion with constant acceleration, but this time uses a formula similar to those used in physics.
Scientists drop a free falling object to make precise measurements. The air resistance is considered negligible. The equation that gives the time from the moment the object is dropped |(t)| as a function of the height of the object |(h)| from the ground is the following. ||t=\sqrt{\frac{-2}{g}(h-h_0)}|| where |g| is the gravitational acceleration, approximately |9.81 \text{ m}/\text{s}^2| on Earth, and |h_0| is the initial height in metres, i.e. the height (from the ground) at which the object is released at |t=0| s.
a) How high was the object released if it hit the ground after |2.473| seconds?
b) If the object is at a height of |10| m after |2.995| seconds, after how long was it at a height of |20| m? How high is the object exactly |1| second before it hits the ground?
It is very important to define the variables if they haven’t been defined already.
|h|, the height of the object (m), is the independent variable. It can be replaced by |x.| |t| , the elapsed time (s), is the dependent variable. It can be replaced by |y| or by |f(x).|
Be careful! |g| and |h_0| are not variables. In fact, |g| is a constant used in physics. Therefore, |\dfrac{-2}{g}| corresponds to the parameter |b| while |h_0| is the parameter |h| of the square root function in standard form.
a)
In this situation, the time |\color{blue}{t}| is |\color{blue}{2{.}473}| s. The height |\color{green}{h}| associated with this instant is |\color{green}{0}| m because the object hits the ground. Therefore, we can say that the square root function passes through the point |(0,\ 2{.}473)|. This point is the |y|-intercept of the function. A sketch of the graph can help visualize the problem.
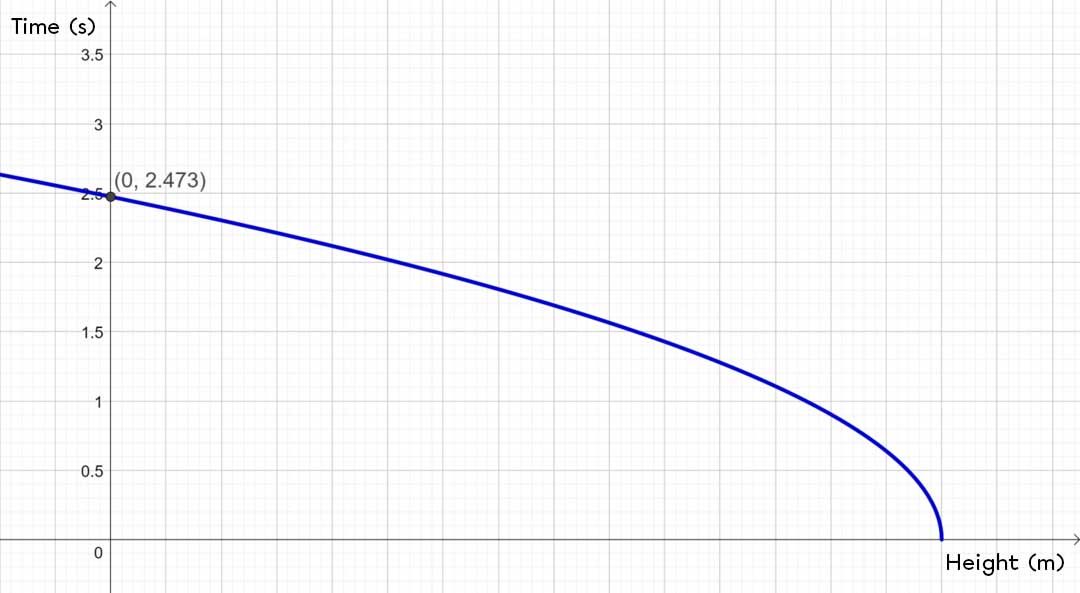
Find the value of |h_0| by substituting in the known values in the equation. ||\begin{align} \color{blue}{t} &=\sqrt{\frac{-2}{g}(\color{green}{h}-h_0)}\\\color{blue}{2.473} &=\sqrt{\frac{-2}{g}(\color{green}{0}-h_0)}\\2.473^2 &=\frac{-2}{g}(-h_0)\\6.116g &=2h_0\\ \frac{6.116g}{2} &= h_0\\30 &\approx h_0 \end{align}||
Answer: The object was released from a height of |30| metres.
Note, at the same time, the coordinates of the vertex of the square root function are |(30,0).|
b)
To answer this question, determine the equation of the function. Therefore, it will be necessary to take advantage of the standard form square root equation. ||\begin{align}\color{magenta}{y} &=\color{purple}{a}\sqrt{\color{blue}{b} (x-\color{red}{h})}+\color{green}{k} \\ \Rightarrow\ \color{magenta}{t} &= \sqrt{\color{blue}{\frac{-2}{g}}(h-\color{red}{h_0})} \end{align}||
We already know that |\color{purple}{a=1}|, |\color{blue}{b=\dfrac{-2}{g}}|, and |\color{green}{k=0}| . Also, the first sentence of the statement gives the coordinates of the point |(10,\ 2{.}995).|
Here is the graphical representation of the problem. It is important to note that |h_0| is not the same as for problem a).
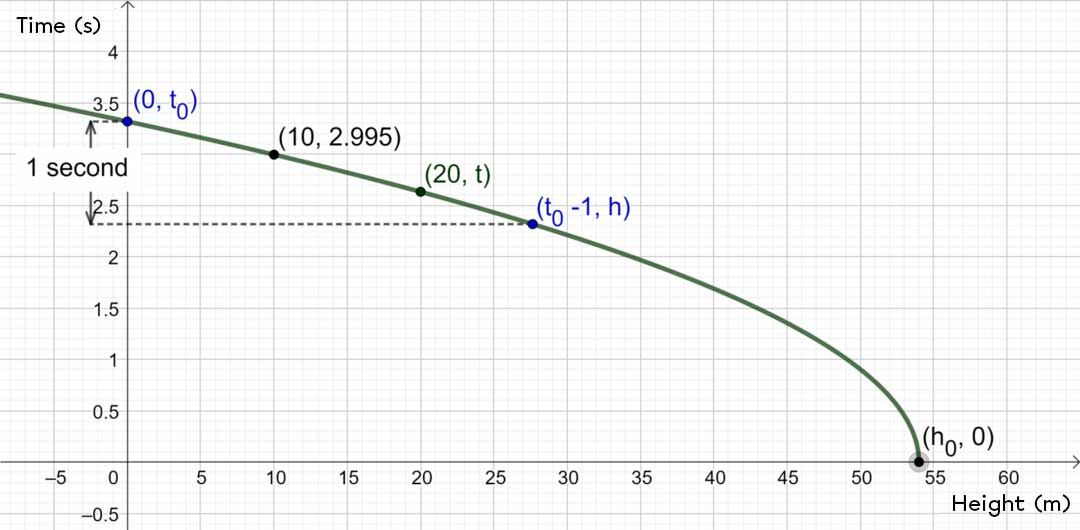
As with a), find the value of |h_0| by replacing the known values in the equation. ||\begin{align}\color{magenta}{t} &=\sqrt{\frac{-2}{g}(\color{blue}{h}-h_0)}\\ \color{magenta}{2.995} &=\sqrt{\frac{-2}{g}(\color{blue}{10}-h_0)}\\2.995^2 &=\frac{-2}{g}(10-h_0)\\8.97g &=-2(10-h_0)\\ \frac{8.97g}{-2} &=10-h_0\\ \frac{8.97g}{-2}-10 &=-h_0\\-54 &\approx -h_0\\ \color{red}{54} &\approx \color{red}{h_0}\end{align}||
Therefore, the equation for question b) is the following. ||t =\sqrt{\frac{-2}{g}(h-\color{red}{54})}||
The first part of the question asks to find the value of |t| when |h=20| metres. Therefore, replace |\color{green}{h}| with |\color{green}{20}| in the equation found. ||\begin{align}t &=\sqrt{\frac{-2}{g}(\color{green}{h}-54)}\\t &=\sqrt{\frac{-2}{g}(\color{green}{20}-54)}\\t &\approx \sqrt{6.9317}\\t &\approx 2.633 \text{ seconds} \end{align}||
The second part of the question asks to find the value of |h| one second before the object hits the ground.
Be careful! Here, |t\neq 1|. The time is measured from the moment when the object is released and not from the time it hits the ground. So, to answer this part of the question, find out when the object touched the ground. Look for |t=?| when |h=0| metres. So, substitute |\color{green}{h}| with |\color{green}{0}| in the equation. ||\begin{align}t &=\sqrt{\frac{-2}{g}(\color{green}{h}-54)}\\t &=\sqrt{\frac{-2}{g}(\color{green}{0}-54)}\\t &\approx 3.318 \text{ seconds} \end{align}||
We find that the moment precisely |1| second before the object touches the ground is |t=3.318-1=2.318| s. Therefore, replace |\color{magenta}{t}| with |\color{magenta}{2.318}| in the equation, then isolate |h|. ||\begin{align}\color{magenta}{t} &=\sqrt{\frac{-2}{g}(h-54)}\\\color{magenta}{2.318} &=\sqrt{\frac{-2}{g}(h-54)}\\2.318^2 &=\frac{-2}{g}(h-54)\\5.373g &=-2(h-54)\\ \frac{5.373g}{-2} &=h-54\\ \frac{5.373g}{-2}+54 &=h\\27{}645 &\approx h \end{align}||
Answers: |2.633| seconds after being released, the object was at a height of |20| metres, and |1| second before touching the ground, the object was at a height of |27.645\ \text{m}.|
In the previous example, there were only equations and not inequalities. A final question with inequalities could have been: "During what time interval is the object at a height of less than |15| metres?" Or, "What is the height of the object when the elapsed time is |2.5| seconds or more?"
To learn how to answer these kinds of questions, see the following concept sheet for more details: Solving a Square Root Equation or Inequality.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction racine carrée de façon interactive, consulte la MiniRécup suivante.
