La résolution de problèmes impliquant la fonction racine carrée

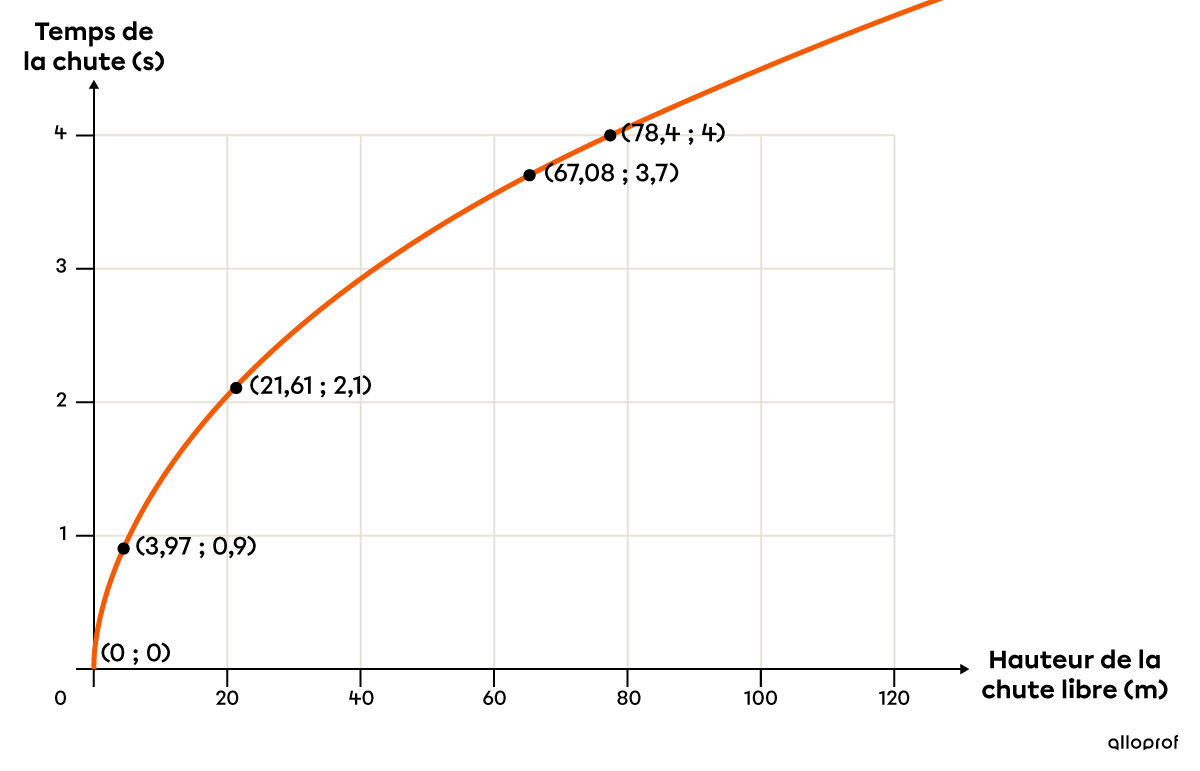
1. Définir les variables

|x :| Hauteur de la chute libre (m)
|f(x):| Temps de la chute (s)

2. Trouver la règle

Puisque la fonction a comme sommet le point |(0,0)|, on peut utiliser le modèle de règle suivant : ||f(x)=a\sqrt{bx}||

Comme la fonction se situe à la droite de son sommet, on conclut que le paramètre b est positif. ||\begin{align} f(x)=a\sqrt{bx}\quad &\Rightarrow \quad f(x)=a\sqrt{\color{red}{\pm} x}\\ &\Rightarrow \quad f(x)=a\sqrt{ x} \end{align}||

Pour trouver le paramètre a, on remplace |x| et |f(x)| par les coordonnées d’un point. On utilise le point |(78{,}4; 4).| ||\begin{align} f(x) &= a\sqrt x \\ 4 &= a\sqrt{78{,}4} \\ 4 &= a(8{,}85...) \\ 0{,}452 &\approx a \\\\ \text{La règle est : }f(x) &=0{,}452\sqrt{x} \end{align}||

3. Calculer |f(381)|, soit |f(x)| lorsque |x=381|
||\begin{align} f(x) &= 0{,}452\sqrt x \\ f(381) &= 0{,}452\sqrt{381} \\ &\approx 8{,}82\ \text{s} \\ \end{align}||

4. Calculer |x| lorsque |f(x)=6{,}61|
||\begin{align} f(x) &= 0{,}452\sqrt x \\ 6{,}61 &= 0{,}452\sqrt{x} \\ \frac{6{,}61}{\color{red}{0{,}452}} &= \frac{0{,}452}{\color{red}{0{,}452}}\sqrt x \\ 14{,}62 &\approx \sqrt x \\ 14{,}62^2 &\approx (\sqrt{x})^2 \\ 214\ \text{m} &\approx \ x \end{align}||

RÉPONSES

a) Si un objet tombe du haut de l’Empire State Building, la chute durera environ |8{,}82\ \text{s}.|

b) Les falaises de Moher ont une hauteur approximative de |214\ \text{m}.|

Il est très important de définir les variables si ce n'est pas déjà fait.

|h|, la hauteur de l'objet (m), est la variable indépendante. Tu peux la remplacer par |x.|
|t|, le temps écoulé (s), est la variable dépendante. Tu peux la remplacer par |y| ou par |f(x).|

Attention! |g| et |h_0| ne sont pas des variables. En fait, |g| est une constante utilisée en Physique. Donc, |\dfrac{-2}{g}| correspond au paramètre |b| tandis que |h_0| est le paramètre |h| de la fonction racine carrée en forme canonique.

a)

Dans cet énoncé, on donne un temps |\color{blue}{t}| de |\color{blue}{2{,}473}| s. La hauteur |\color{green}{h}| associée à cet instant est |\color{green}{0}| m parce qu'on dit que l'objet touche le sol. On peut donc dire que la fonction racine carrée passe par le point |(0;\ 2{,}473)|. Ce point est l'ordonnée à l'origine de la fonction. Une esquisse du graphique peut nous aider à bien visualiser le problème.

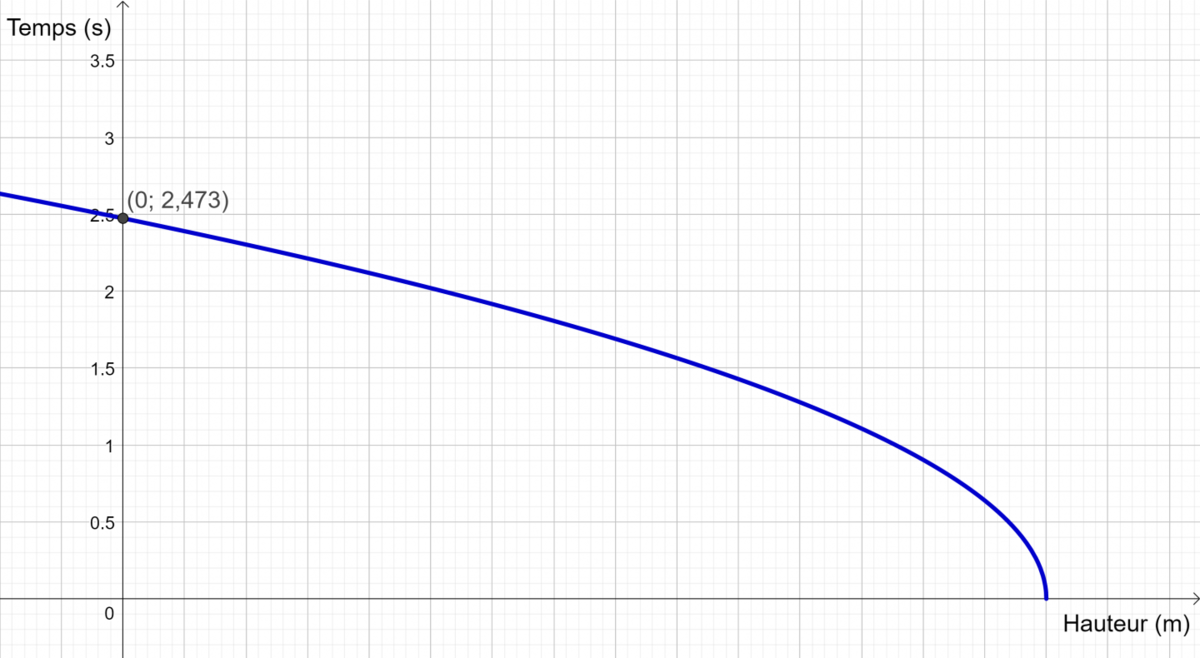
On trouve la valeur de |h_0| en remplaçant les valeurs connues dans l'équation. ||\begin{align} \color{blue}{t} &=\sqrt{\frac{-2}{g}(\color{green}{h}-h_0)}\\\color{blue}{2{,}473} &=\sqrt{\frac{-2}{g}(\color{green}{0}-h_0)}\\2{,}473^2 &=\frac{-2}{g}(-h_0)\\6{,}116g &=2h_0\\ \frac{6{,}116g}{2} &= h_0\\30 &\approx h_0 \end{align}||

Réponse : L'objet a été relâché d'une hauteur de |30| m.

Fait à noter, on a, du même coup, trouvé les coordonnées du sommet de la fonction racine carrée : |(30,0).|

b)

Pour répondre à cette question, il faut déterminer l'équation de la fonction. Il sera donc nécessaire d'utiliser la forme canonique : ||\begin{align}\color{magenta}{y} &=\color{purple}{a}\sqrt{\color{blue}{b} (x-\color{red}{h})}+\color{green}{k} \\ \Rightarrow\ \color{magenta}{t} &= \sqrt{\color{blue}{\frac{-2}{g}}(h-\color{red}{h_0})} \end{align}||

On sait déjà que |\color{purple}{a=1}|, |\color{blue}{b=\dfrac{-2}{g}}| et que |\color{green}{k=0}|. Aussi, la première phrase de l'énoncé donne les coordonnées du point |(10;\ 2{,}995).|

Voici la représentation graphique de ce problème. Il est important de remarquer que |h_0| n'est pas le même que pour le problème a).

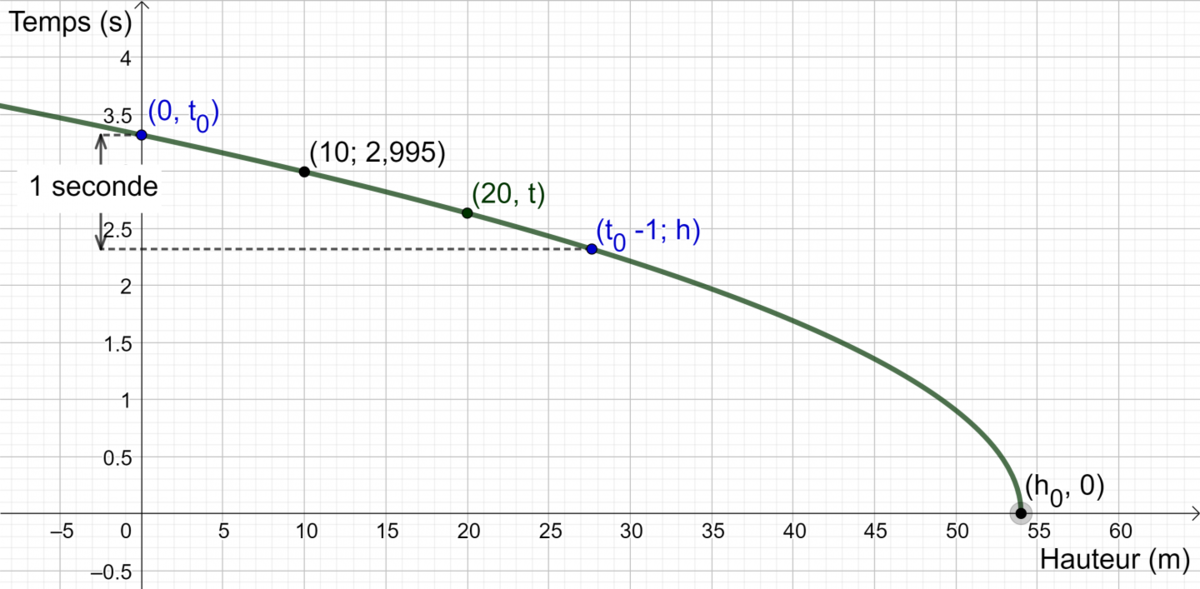
Comme pour le a), on trouve la valeur de |h_0| en remplaçant les valeurs connues dans l'équation. ||\begin{align}\color{magenta}{t} &=\sqrt{\frac{-2}{g}(\color{blue}{h}-h_0)}\\ \color{magenta}{2{,}995} &=\sqrt{\frac{-2}{g}(\color{blue}{10}-h_0)}\\2{,}995^2 &=\frac{-2}{g}(10-h_0)\\8{,}97g &=-2(10-h_0)\\ \frac{8{,}97g}{-2} &=10-h_0\\ \frac{8{,}97g}{-2}-10 &=-h_0\\-54 &\approx -h_0\\ \color{red}{54} &\approx \color{red}{h_0}\end{align}||

La règle de la fonction pour la question b) est donc : ||t =\sqrt{\frac{-2}{g}(h-\color{red}{54})}||

La première sous-question demande de trouver la valeur de |t| lorsque |h=20| m. Il faut donc remplacer |\color{green}{h}| par |\color{green}{20}| dans la règle trouvée. ||\begin{align}t &=\sqrt{\frac{-2}{g}(\color{green}{h}-54)}\\t &=\sqrt{\frac{-2}{g}(\color{green}{20}-54)}\\t &\approx \sqrt{6{,}9317}\\t &\approx 2{,}633 \text{ secondes} \end{align}||

La deuxième sous-question demande de trouver la valeur de |h| une seconde avant que l'objet ne touche le sol.

Attention! Ici, |t\neq 1|. En effet, le temps est mesuré à partir du moment où l'objet est relâché et non à partir du temps où il touche le sol. Donc, pour répondre à cette sous-question, il faut d'abord trouver à quel instant l'objet a touché le sol. On cherche donc |t=| ? lorsque |h=0| m. On remplace donc |\color{green}{h}| par |\color{green}{0}| dans la règle. ||\begin{align}t &=\sqrt{\frac{-2}{g}(\color{green}{h}-54)}\\t &=\sqrt{\frac{-2}{g}(\color{green}{0}-54)}\\t &\approx 3{,}318 \text{ secondes} \end{align}||

On en déduit que l'instant précis, |1| seconde avant de toucher le sol, est |t=3{,}318-1=2{,}318| s. Il faut donc remplacer |\color{magenta}{t}| par |\color{magenta}{2{,}318}| dans la règle, puis on doit isoler |h|. ||\begin{align}\color{magenta}{t} &=\sqrt{\frac{-2}{g}(h-54)}\\\color{magenta}{2{,}318} &=\sqrt{\frac{-2}{g}(h-54)}\\2{,}318^2 &=\frac{-2}{g}(h-54)\\5{,}373g &=-2(h-54)\\ \frac{5{,}373g}{-2} &=h-54\\ \frac{5{,}373g}{-2}+54 &=h\\27{,}645 &\approx h \end{align}||

Réponses : |2{,}633| secondes après avoir été relâché, l'objet était à une hauteur de |20| m et |1| seconde avant de toucher le sol, l'objet était à une hauteur de |27{,}645\ \text{m}.|