Solving Problems Involving Rational Functions

To properly manage staff, the manager of a pharmacy studies their customer’s habits. They want to compare the number of customers who enter the pharmacy on weekends and the number who come on weekdays. For example, on Wednesdays between 9 a.m. and 9 p.m., the number of clients varies depending on the function |f(x)=3x-10,| where |x| is the time of day. For the same period of time on Saturdays, the number of clients varies according to the function |g(x)=9x-65.|

At what time are there twice as many customers on Saturday as on Wednesday?

1. Build the rational function
   The general procedure of the question is to take the number of customers on Saturday (|g(x)|) and divide it by those on Wednesday (|f(x)|). Therefore:
   ||\begin{align}\text{ratio of clients} & = && \dfrac{g(x)}{f(x)} \\\\ h(x) & = && \dfrac{9x-65}{3x-10} \end{align}||

2. Draw a sketch of the function
   To confirm the previous argument, it is preferable to sketch a graph. The rational function should be in its standard form, as follows.

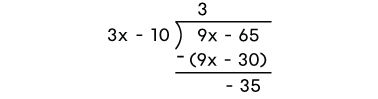
Therefore, the following is obtained.
||\begin{align}
h(x) &= &&\dfrac{-35}{3x-10} + 3\\\\
&=&& \dfrac{-35}{3\left(x-\dfrac{10}{3}\right)} + 3 \end{align}||

With |(h,k) = \left(\dfrac{10}{3},3\right)| and |a < 0,| we get the sketch below.

3. Solve the equation
   Since we want to know when the ratio is |2,| we replace |h(x)| by |2| in the initial rational function, resulting in:
   ||\begin{align}
   2 &= && \dfrac{9x-65}{3x-10} \\\\2 \color{red}{(3x-10)} & = && \dfrac{9x-65}{3x-10} \color{red}{(3x-10)}\\\\
   6x ^{\color{blue}{-9x}} - 20 _{\color{red}{+20}}& = && 9x^{\color{blue}{-9x}} -65 _{\color{red}{+20}} \\\\
   \dfrac{-3x}{\color{red}{-3}} & = && \dfrac{-45}{\color{red}{-3}} \\\\
   x & = && 15 \end{align}||

4. Interpret the results
   There are twice as many customers at 3 p.m. on Saturday as there are on Wednesday.