La résolution de problèmes impliquant la fonction rationnelle

Afin de bien gérer son personnel, le gérant d'une pharmacie étudie le mouvement de sa clientèle. En fait, il s'intéresse à la comparaison entre le nombre de clients qui viennent à son magasin la fin de semaine et celui des clients qui le visitent en semaine. Par exemple, le mercredi, l'achalandage varie selon la fonction |f(x)=3x-10|, où |x| est l'heure du jour. Pour la même période de temps, soit de 9 h à 21 h, le nombre de clients varie selon la fonction |g(x)=9x-65| durant la journée du samedi. 

À quelle heure y a-t-il 2 fois plus de clients le samedi que le mercredi?

1) Construire la fonction rationnelle
L'idée générale de la question est de prendre le nombre de clients du samedi (|g(x)|) et de le diviser par ceux du mercredi (|f(x)|). Ainsi:
||\begin{align}\text{ratio des clients} & = && \frac{g(x)}{f(x)} \\\\ h(x) & = && \frac{9x-65}{3x-10} \end{align}||

2) Tracer une esquisse de la fonction 
Pour valider le raisonnement précédent, il est préférable de tracer un graphique. Pour y arriver, la fonction rationnelle sous sa forme canonique est à privilégier:

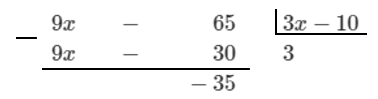
Ainsi, on obtient
||\begin{align}
h(x) &= &&\frac{-35}{3x-10} + 3\\\\
&=&& \frac{-35}{3\left(x-\frac{10}{3}\right)} + 3 \end{align}||
Avec |(h,k) = \left(\frac{10}{3},3\right)| et |a < 0|, on obtient l'esquisse suivante:

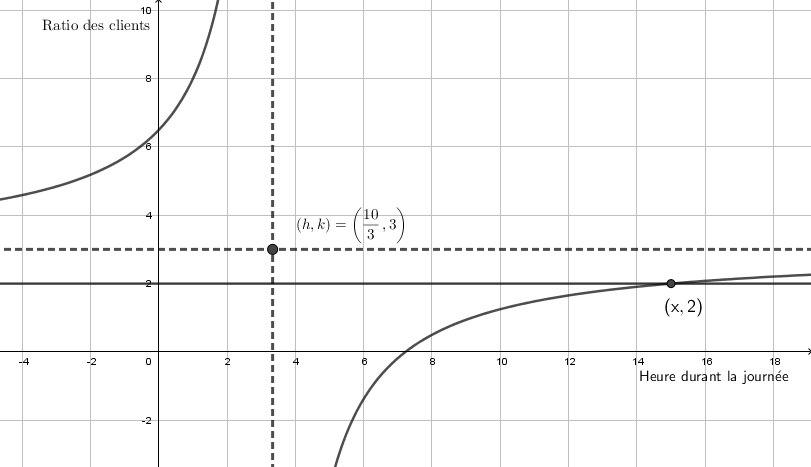
3) Résolution de l'équation
Puisqu'on veut savoir à quel moment le ratio est de 2, on remplace |h(x)| par 2 dans la fonction rationnelle initiale et on obtient :
||\begin{align}
2 &= && \frac{9x-65}{3x-10} \\\\2 \color{red}{(3x-10)} & = && \frac{9x-65}{3x-10} \color{red}{(3x-10)}\\\\
6x ^{\color{blue}{-9x}} - 20 _{\color{red}{+20}}& = && 9x^{\color{blue}{-9x}} -65 _{\color{red}{+20}} \\\\
\frac{-3x}{\color{red}{-3}} & = && \frac{-45}{\color{red}{-3}} \\\\
x & = && 15 \end{align}||

4) Interpréter le résultat obtenu
À 15 h, il y a 2 fois plus de clients le samedi que le mercredi.