When segments intersect a circle, they sometimes form angles. We qualify the angles in four different ways depending on their position in the circle.
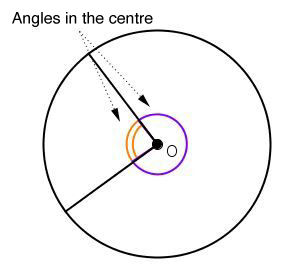
A central angle is an angle formed by two radii of a circle. The vertex of the angle is the centre of the circle.
The orange and purple angles in the following circle are central angles, since they are formed by two radii of the circle.
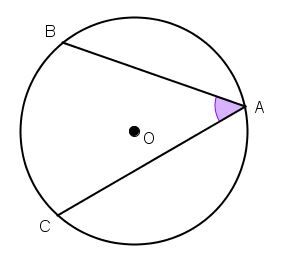
An inscribed angle is an angle with a vertex located on a circle and whose sides contain chords of the circle.
The angle BAC in the following diagram is an angle inscribed in the circle with centre O.
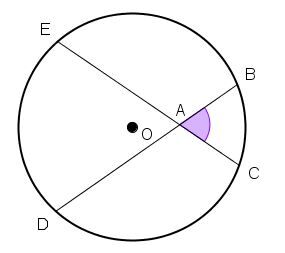
An interior angle is an angle formed by two chords intersecting inside a circle.
The angle BAC in the following diagram is an interior angle of the circle with centre O.
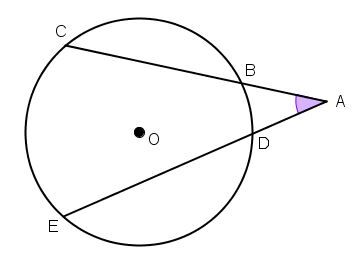
An exterior angle is an angle with a vertex outside of a circle whose sides are secants or tangents to the circle.
The angle CAE in the following diagram is an angle outside the circle with centre O.
There are metric relationships in the circle that involve the angles described above.